2.12 Задача о брахистохроне

Задача о брахистохроне (от греческого brachistos- кратчайший и chronos- время), или о кривой скорейшего спуска- одна из первых вариационных задач, была поставлена швейцарским математиком И.Бер-нулли в 1696 году и заключа­лась в следующем [3].

В вертикальной плоскости даны две точки А и В не лежащие на од­ной вертикали. Требуется среди всех кривых, проходящих через указанные точки, найти такую, спускаясь по которой под действием силы тяжести, материальная точка скатится из точки А в точку В за кратчайшее время (рис. 14).

Исходя из закона сохранения энергии, считаем, что скорость, достигнутая шариком на заданном уровне, зависит только от потери потенциальной энергии при достиже­нии этого уровня, а не от вида траектории, по которой скатывается шарик. Это означает, что . C другой стороны, геометрические построения показывают, что

.

Используя оптико-меха­ническую аналогию , можно записать, что . Данное уравнение и есть диф­ференциальное уравнение брахистохроны.

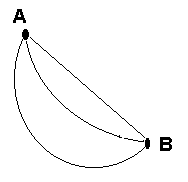
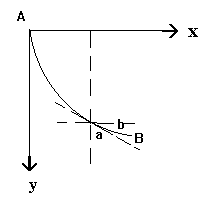
Рис.14. К выводу уравнения брахистохроны

Эта задача знаменита тем, что, помимо значимости ее решения с точки зре­ния естественнонаучной, она стала источником идей совершенно новой области математики^_ вариационного исчисления. Эта задача решалась математиками раз­ных времен и всегда получалась хорошо известная кривая^_ циклоида. Действительно, после разделения переменных, получаем уравнение вида:

.

Введем теперь новую переменную "ф", полагая .

Тогда преобразования координат будут иметь вид:

Интегрирование последнего уравнения приводит к соотношению: , где в силу начальных условий x = y = 0 при ф=0 и постоян­ная С₁=0.

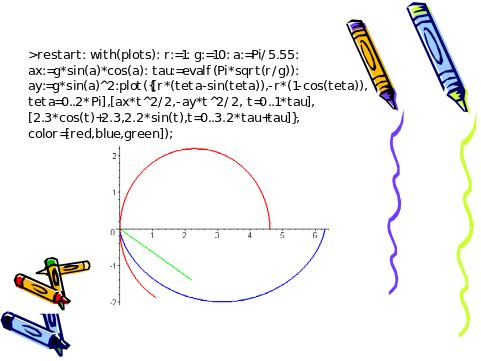
Слайд 11. Иллюстрация экстремальной траектории в поле тяготения

В результате интегрирования имеем:

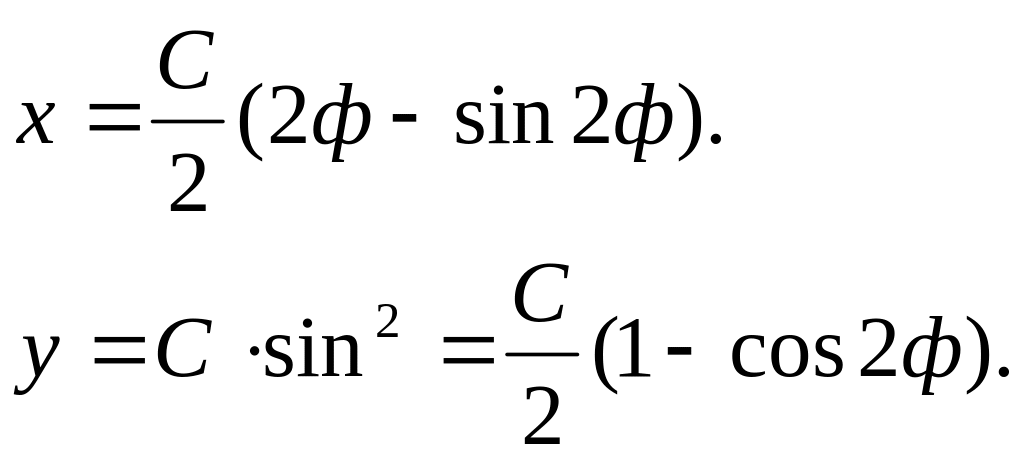
Полагая здесь С/2 = r, 2ф = приходим к стандартным параметрическим уравнениям циклоиды:

Указание. Построить экстремальную траекторию, используя интерактивную графику; сравнить время движения по другим траекториям. Рассмотреть движение по наклонной прямой и дуге эллипса.

2.13 Управление таймером в режиме реального времени

Для отслеживания интервалов времени в ПК имеется специальное устройство- системный таймер. Это электронные часы, которые можно программно устанавливать, опрашивать, использовать в качестве «будильника» для выдачи сигнала процессору в заданное время или как прибор для измерения интервалов времени между внешними событиями. В системах программирования для этого имеются специальные процедуры управления таймером [43].

Слайд 12. Точность временной задержки в Pascal- программе

В ПК системный таймер работает с частотой 18,2 Гц, что обеспечивает точность на уровне 55 ms. Например, при измерении ускорения свободного падения с высоты ~1м в учебной лаборатории или измерении времени реакции человека на сигнал (0,2- 0,3 с) данной точности недостаточно.

Один из способов повышения точности измерения времени состоит в перепрограммировании системного таймера. Его частоту можно увеличить до 8192 Гц и более, а точность- до ~10^-4 с и точнее. В статье Г.Г.Матаева приводится модуль на языке Паскаль для перепрограммирования системного таймера [25].