4.9 Иерархия временных масштабов в броуновской динамике

Развитие методологического подхода к изучению броуновской динамики с использованием иерархии временных масштабов можно найти в учебном пособии [44]. Причем компьютерная визуализация решений дает наглядное представление о математическом моделировании рассматриваемого стохастического процесса не только в одномерном случае или на плоскости, но и в пространстве трех измерений.

Траектория движения броуновской частицы представляет собой ломаную линию, прямолинейные участки которой соответствуют временам движения порядка . Ясно, что регистрация отдельных прямолинейных участков траектории невозможна. Поэтому каждый из участков, фиксируемых нами (наблюдаемых визуально) как прямой, на самом деле является ломаной линией со временем прохождения примерно с, тогда как время эксперимента составляет ~ 30 с.

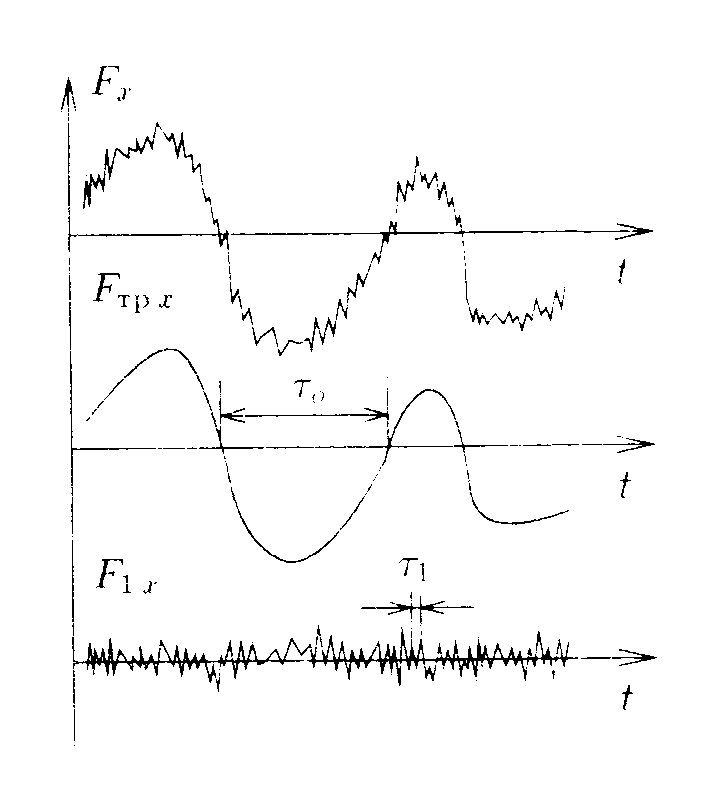
Рис.44. Иерархия временных масштабов

в броуновской динамике

При характерных массах ~ кг броуновские частицы на 8-9 порядков тяжелее молекул, поэтому соударение с отдельной молекулой не может вызвать значительного изменения скорости такой частицы. С учетом этого правильнее говорить о флуктуациях давления среды, влияние которых возрастает с уменьшением размера броуновской частицы. В то же время, поскольку сами флуктуации обусловлены молекулярной структурой вещества, броуновское движение можно считать прямым и доступным для визуального наблюдения проявлением движения молекул [44].

Характерное время изменения силы, действующей на частицу, можно оценить как отношение среднего расстояния между молекулами (~ м) к средней скорости их теплового движения (~ м/с). Отсюда получаем с, что на несколько порядков меньше времени релаксации скорости.

Такое значительное отличие временных интервалов позволяет разложить силу , действующую на броуновскую частицу со стороны среды, на две независимых компоненты: силу вязкого трения , изменяющуюся вместе со скоростью за время с, и случайную (стохастическую) силу с характерным временем изменения с. Среднее значение силы за время равно нулю. На рис. 44 качественно (без соблюдения масштаба) представлены зависимости проекций сил , и на ось от времени.

Уравнение движения броуновской частицы в проекции на ось с учетом сил и имеет вид:

Умножим обе части данного уравнения на и, учитывая, что

и

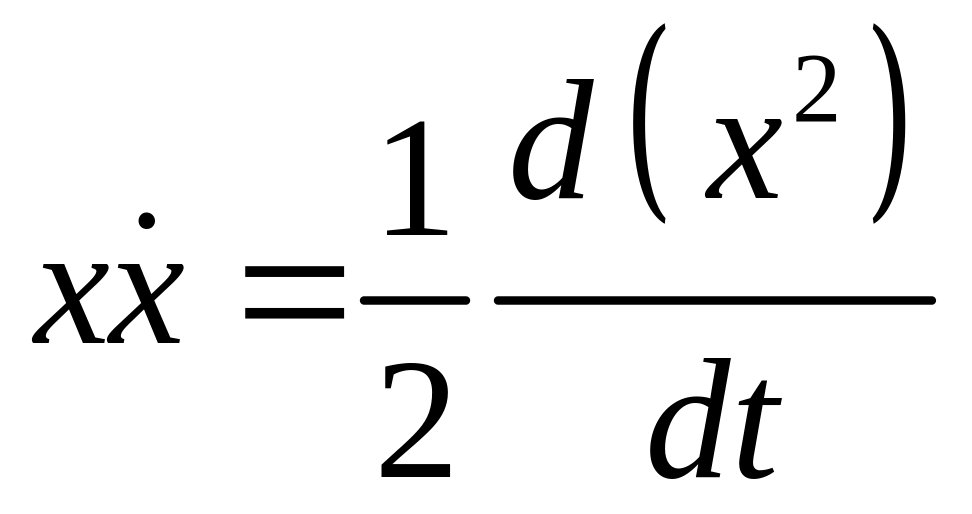
преобразуем динамическое уравнение к виду:

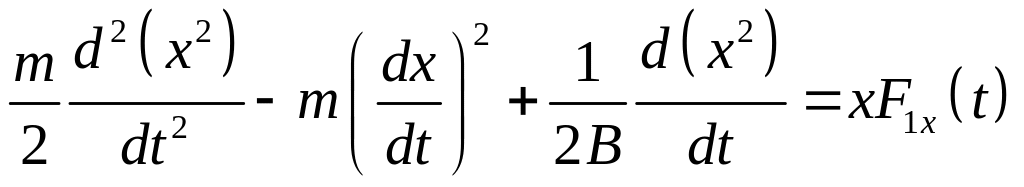
Усредним полученное уравнение по множеству частиц. При этом учтем, что, согласно теореме о равномерном распределении энергии по степеням свободы,

и

,

поскольку случайный характер силы приводит к тому, что в ансамбле частиц распределение ее проекции будет симметричным относительно нуля. Из статистических соображений можно показать, что плотность распределения случайной силы четная функция с нулевым средним значением.

Таким образом, в результате усреднения получаем:

Вводя обозначение

,

разделим переменные и проинтегрируем данное дифференциальное уравнение:

,

где – постоянная интегрирования.

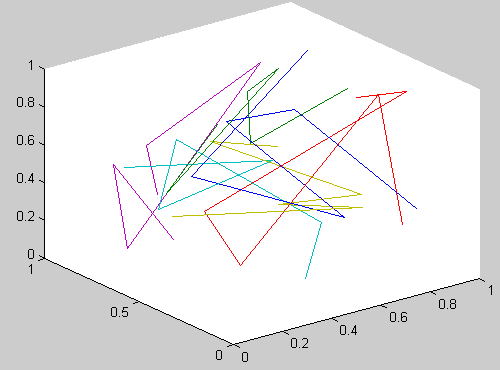
Рис.45. Траектория движения броуновских частиц

в графике MatLab

Реальные измерения проводятся за промежутки времени, намного превышающие с, поэтому второе слагаемое в последнем выражении можно отбросить. Тогда

,

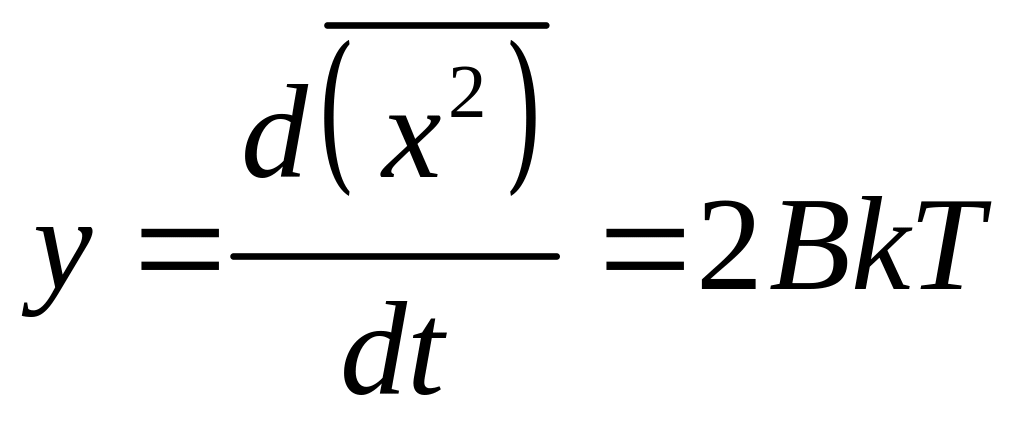и , если отсчитывать смещение с момента . Полученное выражение называется формулой Эйнштейна- Смолуховского.

Заметим, что решение задачи о движении броуновских частиц зависит от размерности. В общем случае решение имеет вид:

,

где - коэффициент диффузии, зависящий от температуры; - размерность пространства. Т.е. в трехмерном случае средний квадрат радиуса-вектора частиц .