
- •А.И. Ходанович математическое моделирование на компьютере
- •История математического моделирования на компьютере
- •Задачи аналитического и численного моделирования
- •1. Симметрия и модели с числовыми последовательностями
- •1.1 Формула пути равнопеременного движения
- •1.3 «Золотое сечение» и числа Фибоначчи
- •1.4 Сопротивление бесконечной электрической цепи
- •1.5 Сопротивление конечной электрической цепи
- •1.6 «Золотое сечение» в поле тяготения
- •Равенство тяжелой и инертной массы в свободном падении
- •2.2 Реальная динамика тела в среде
- •2.3 Цепная линия и метод кратных скобок Пуассона
- •2.4 Баллистическая кривая
- •2.5 Модели космической динамики
- •2.6 Посадка «Гюйгенса» на Титан
- •Задача Кеплера
- •Слайд 10. Компьютерно-графическое моделирование в небесной механике
- •2.8 Орбита в пространстве скоростей
- •2.9 Конические сечения в поле тяготения
- •2.10 Прецессия орбиты при малом возмущении
- •2.11 Задача трех тел в небесной механике
- •2.12 Задача о брахистохроне
- •Слайд 11. Иллюстрация экстремальной траектории в поле тяготения
- •2.13 Управление таймером в режиме реального времени
- •2.14 Физический опыт и модель измерений
- •2.15 Водяные часы
- •2.16 Фракталы в комплексной плоскости
- •Слайд 14. Комплексные отображения в нелинейной динамике
- •3. Колебания и адиабатические инварианты
- •3.1 Гармонический осциллятор
- •3.2 Задача «Бездонный колодец»
- •3.3 Фигуры Лиссажу
- •3.4 Параметрические колебания
- •3.5 Маятник Капицы
- •3.6 Хаотическое поведение маятника и отображение Пуанкаре
- •3.8 Задача с соударениями
- •3.9 Хаотические колебания при соударениях
- •3.10 Представление колебаний рядом Фурье
- •3.11 Два тела на пружине
- •3.12 Цепочка Ферми-Паста-Улама
- •3.13 Линейная цепочка связанных осцилляторов
- •3.14 Колебания мембраны в интерактивной графике
- •3.15 Вращение частицы в трехмерной графике
- •4. Вероятностно-статистическая линия математического моделирования
- •4.1 Нормальное распределение и статистический критерий
- •4.2 Распределение расстояний между молекулами газа
- •4.3 Радиоактивный распад изотопа
- •4.4 Флуктуации и биномиальный случай
- •4.5 Статистическое распределение с бесконечной дисперсией
- •4.6 Закон больших чисел и центральная предельная теорема
- •4.7 Статистические усреднения в эксперименте
- •4.8 Диффузия в модели случайных блужданий
- •4.9 Иерархия временных масштабов в броуновской динамике
- •4.10 Метод Монте-Карло с генератором случайных чисел
- •4.11 Алгоритмы числа
- •4.12 Модели плоских фигур
- •4.13 Площадь круга с малым возмущением
- •4.14 «Игла Бюффона»
- •4.15 Выделение сигнала на фоне «шумов»
- •4.16 Регрессионная модель эксперимента и метод наименьших квадратов
- •4.17 Модели линейной регрессии в планировании эксперимента
- •5. Дидактические игры математического моделирования
- •5.1 «Телепат»
- •5.2 Игрушка «Раскидай»
- •5.3 Игрушка «Ванька-встанька»
- •5.4 Игра Баше
- •5.5 «Перевернутая» игра Баше
- •5.6 Игра в 15
- •Литература
- •Ходанович
4.8 Диффузия в модели случайных блужданий
О
В реальном кристалле могут происходить события, после которых формула «взаимно- однозначное соответствие» становится неверной: в кристалле появляются узлы, где нет атомов, и атомы, которые расположены не в узлах. Узлы, свободные от атомов, в кристалле. Таким образом, возникают «вакансия» и «межузельный атом». Они обретут структурную самостоятельность лишь тогда, когда удалятся друг от друга на расстояние, достаточное для того, чтобы для межузельного атома оставленный им узел был бы не «своим», не избранным, а одним из множества других аналогичных вакантных узлов. Вакансию и межузельный атом, потерявший родственную связь, называют «парой Френкеля» [14].
Вакансии и межузельные атомы часто объединяют общим названием «точечные дефекты». Название, разумеется, очень условное. Они «точечными» не были бы и в том случае, если бы их появление никак не искажало кристаллическую решетку. А в действительности искажает. О том, что имеется вакантный узел или межузельный атом, известно на большом расстоянии от них.
Вакансионный механизм самодиффузии происходит и тогда, когда он не приводит ни к каким видимым последствиям,- свойства и структура кристалла остаются неизменными. Такой процесс осуществляется в «равновесном» кристалле, свободном от любых неоднородностей. Происходит оно лишь вследствие флуктуации энергии. Флуктуации- причина образований вакансий, они же причина перескока атома в соседнюю вакансию или в соседнюю межузельную ячейку. Такой перескок (случайное блуждание) и является элементарным актом самодиффузии.
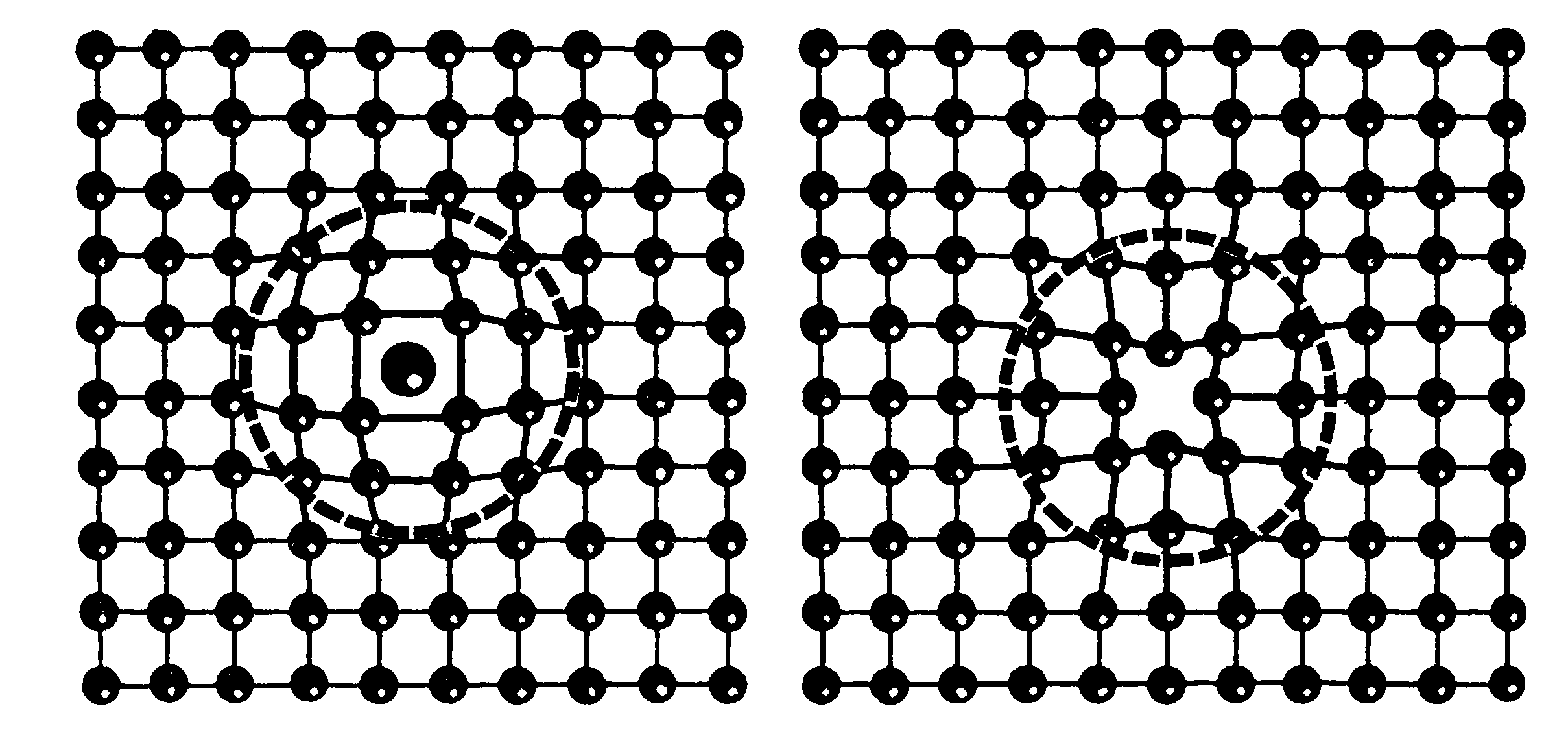
Рис.40. «Точечные дефекты» в кристаллической решетке
Первоначальную формулировку задачи о «случайных блужданиях» предложил Пирсон в 1906 г. Если человек случайным образом делает N шагов равной длины от фонарного столба в произвольных направлениях, то, как далеко отойдет он от этого столба? (рис.41). Со времени такой формулировки статистической задачи модели случайного блуждания получили широкое распространение в физике, биологии и общественных науках. Хорошо знакомыми по учебникам приложениями являются диффузия молекул в газе и броуновское движение коллоидных взвесей в жидкости, моделирование длинных полимерных цепочек [16].


Рис. 41. Иллюстрация постановки задачи о случайных блужданиях
Для
простоты рассмотрим одномерные случайные
блуждания частицы с постоянным шагом.
Пусть в результате n
таких
последовательных шагов частица оказалась
в точке с координатой
![]() .
Тогда после очередного шага она попадет
в точку
.
Тогда после очередного шага она попадет
в точку
![]() .
Поскольку при равновероятных блужданиях
средняя координата
.
Поскольку при равновероятных блужданиях
средняя координата
![]() найдем величину, которой можно
охарактеризовать среднее удаление
частицы. Очевидно,- это среднее значение
квадрата смещения
найдем величину, которой можно
охарактеризовать среднее удаление
частицы. Очевидно,- это среднее значение
квадрата смещения
![]() .
.
Используя
метод математической индукции, на основе
полученного соотношения легко показать,
что
![]() .
Предположить данную зависимость можно
из результатов реального или виртуального
компьютерного эксперимента (рис. 42).
Заметим, что реальный эксперимент
проводился несколько часов с десятью
«частицами», в то время как более точный
вычислительный эксперимент длится
несколько минут при значительно больших
параметрах и легко воспроизводится на
современном ПК.
.
Предположить данную зависимость можно
из результатов реального или виртуального
компьютерного эксперимента (рис. 42).
Заметим, что реальный эксперимент
проводился несколько часов с десятью
«частицами», в то время как более точный
вычислительный эксперимент длится
несколько минут при значительно больших
параметрах и легко воспроизводится на
современном ПК.
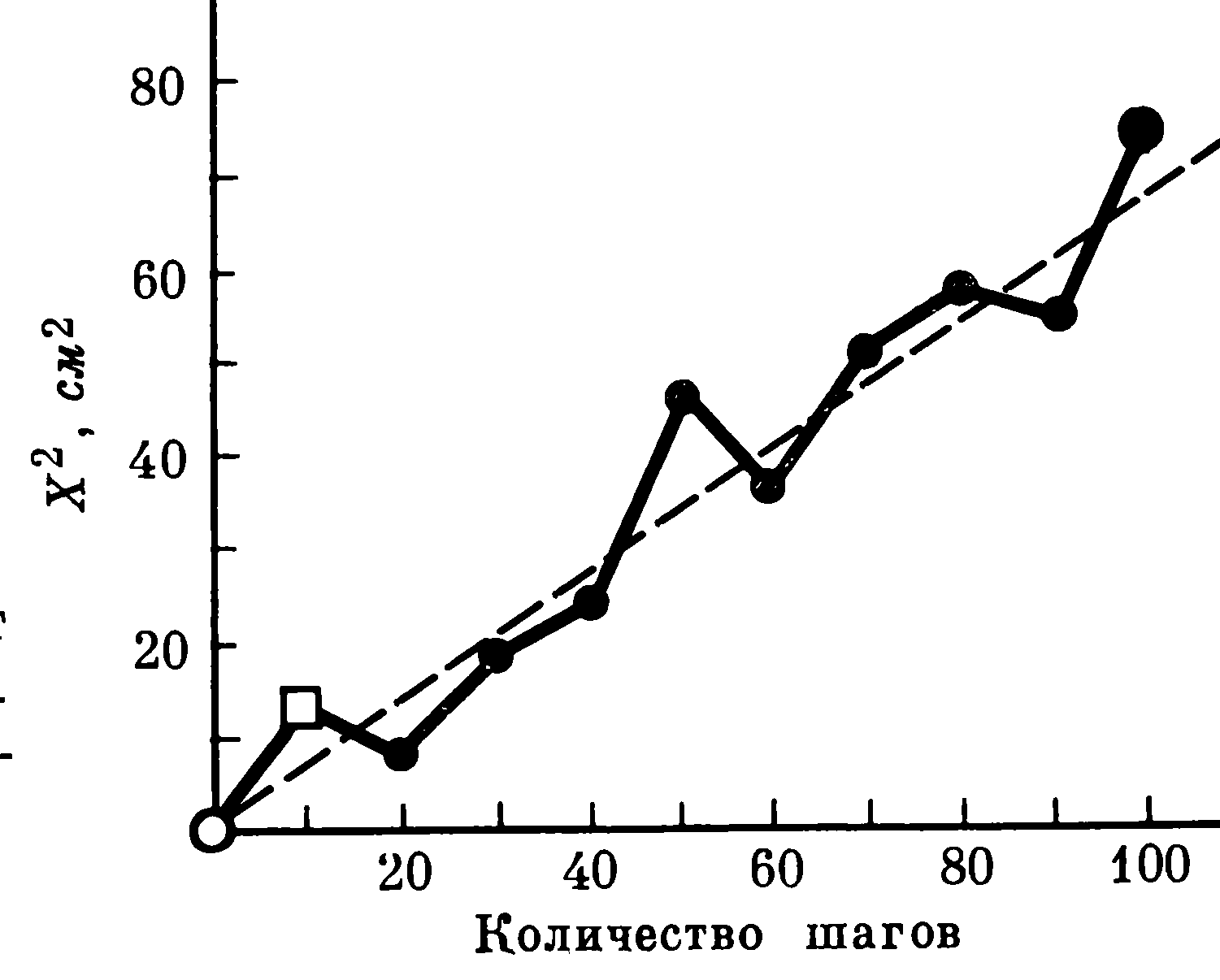
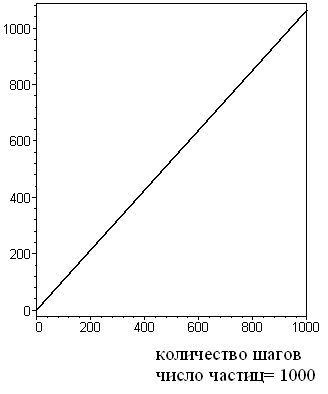
Рис. 42. Закон случайных блужданий
в физическом эксперименте
Таким
образом, среднее значение квадрата
смещения пропорционально числу
шагов, а если шаги совершаются за
одинаковые промежутки времени,
следовательно,
![]() .
Диффузия частиц такова, что средний
квадрат
смещения
растет пропорционально времени. Другими
словами, квадратный корень
.
Диффузия частиц такова, что средний
квадрат
смещения
растет пропорционально времени. Другими
словами, квадратный корень
![]() растет
со временем пропорционально
растет
со временем пропорционально
![]() .
Эта величина, называемая средним
квадратичным значением координаты,
не
равна среднему значению расстояния
частицы от начала координат спустя
промежуток времени t
и в многомерном случае.
.
Эта величина, называемая средним
квадратичным значением координаты,
не
равна среднему значению расстояния
частицы от начала координат спустя
промежуток времени t
и в многомерном случае.
Поучительно
рассмотреть непрерывный предел модели
одномерного случайного блуждания.
Если с равной вероятностью делается
шаг вправо или влево, то случайное
блуждание можно переписать в виде
простого «порождающего» уравнения
![]() или
с учетом длины и времени шага для
плотности вероятности имеем
или
с учетом длины и времени шага для
плотности вероятности имеем
![]() .
После несложных преобразований получим
конечно-разностное уравнение диффузии,
которое в пределе
.
После несложных преобразований получим
конечно-разностное уравнение диффузии,
которое в пределе
![]() и
и
![]() переходит в дифференциальное уравнение
в частных производных
переходит в дифференциальное уравнение
в частных производных
![]() ,
где коэффициент диффузии
,
где коэффициент диффузии
![]() [3].
[3].
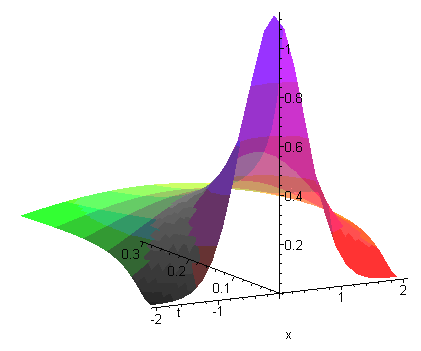
Рис. 43. Нормальный закон диффузии в трехмерной графике
Решением данного уравнения для свободного пространства является распределение Гаусса (нормальный закон):
![]() (рис.
43).
(рис.
43).
Таким
образом,
![]() ,
а
,
а
![]() .
Обобщение решения на d-мерный
случай дает:
.
Обобщение решения на d-мерный
случай дает:
![]() .
.
