3.4 Параметрические колебания

Если один из параметров колебательной системы (например, приведенную длину маятника) изменять с частотой вдвое большей, чем собственная частота колебаний этой системы, то энергия от источника двойной частоты перекачивается в энергию собственных колебаний.

При модуляции длины подвеса, с частотой, близкой к удвоенной собственной частоте, в отсутствие трения маятник раскачивается, наблюдается параметрический резонанс.

Без ограничения общности достаточно рассмотреть уравнение вида: . Математическое моделирование параметрического резонанса приводит к уравнению Матьё: при .

Указание. В качестве примера можно рассмотреть «качели» с собственной частотой математического маятника . Покажите, что если приседать в край­них точках два раза за период, так что длина будет в этих точках увеличиваться по сравнению с начальной длиной, то амплитуда колебаний (качаний) будет воз­растать. Напишите уравнение вращательного движения качелей , где J- момент инерции, - угол, - момент силы. Положите , где а<<1.

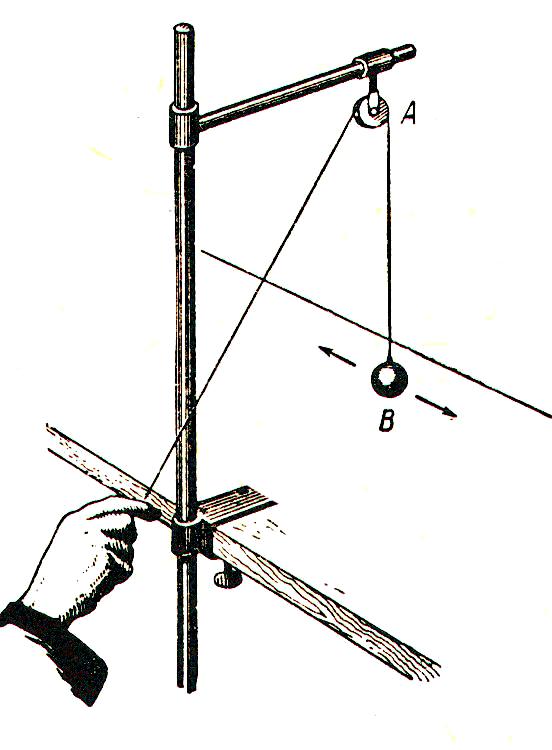
Рис.22. Эксперименты с параметрическими колебаниями

3.5 Маятник Капицы

Маятником Капицы называется математический маятник, прикрепленный к точке подвеса, которая совершает быстрые вертикальные и горизонтальные осцилляции. При определенных условиях, наложенных на амплитуды и частоты осцилляций, возникают дополнительные положения устойчивого равновесия маятника. Маятник Капицы весьма удобен для изучения явления параметрического резонанса, он достаточно легко воспроизводится в лабораторных условиях и обстоятельно описан теоретически. В 1951 году П.Л. Капица предложил метод усреднения по быстро осциллирующим переменным, суть которого продемонстрируем на примере движения маятника с быстро осциллирующей точкой подвеса.

Случай 1.

Т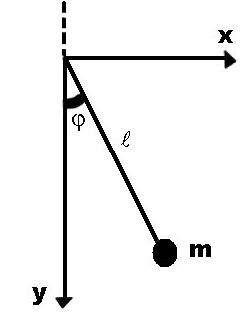 очка подвеса маятника совершает вертикальные колебания с большой частотой

.

Потенциальная энергия груза задается выражением

,

где m – масса груза, g – ускорение свободного падения, l – длина нити,  угловая переменная осцилляций (отклонение от вертикали).

Запишем уравнения движения маятника по осям X и Y:

Определим лагранжиан: , .

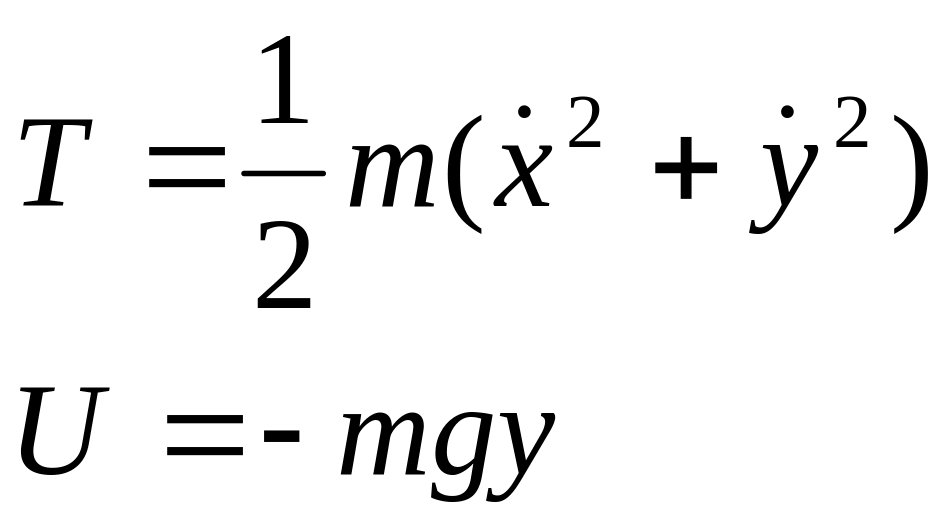Выполним несложные преобразования:

Кинетическая энергия: .

Опускаем полную производную по времени .

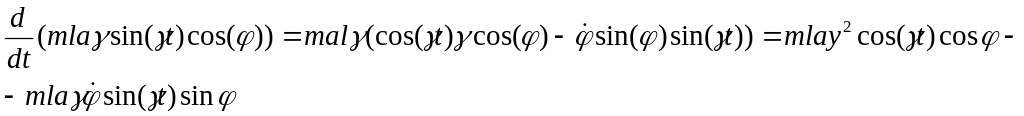Отсюда следует, что

Подставляем в выражение для кинетической энергии и опускаем все полные производные по времени:

Таким образом, лагранжиан равен:

Учитывая, что , а

, или

Подставляя f в выражение для компоненты, отвечающей за быстрые осцилляции, получаем:

и находим среднеквадратичную скорость этих колебаний:

. Таким образом:

.

Каждому устойчивому положению равновесия отвечает минимум эффективной потенциальной энергии.

Условия глубокой высокочастотной модуляции: , приводят к появлению нового устойчивого равновесного положения  =  (вертикально вверх).

Случай 2

Т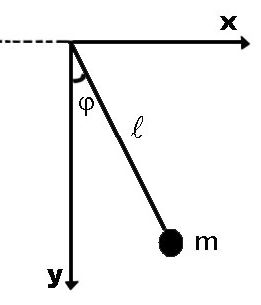 очка подвеса совершает горизонтальные колебания с большой частотой.

Запишем уравнения движения маятника относительно осей: , .

Определим лагранжиан: , .

Выполним несложные преобразования для выводы формулы кинетической энергии:

Итак, кинетическая энергия:

Опускаем полную производную по времени ;

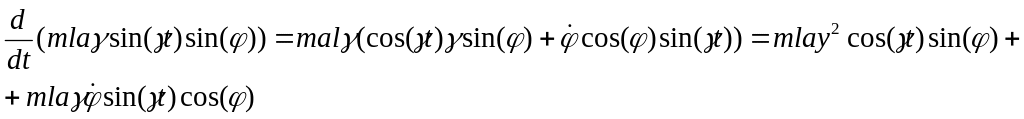Отсюда следует, что .

Подставляем в выражение для кинетической энергии и опускаем все полные производные по времени:

.

Лагранжиан равен: .

Учитывая, что , а , где .

Подставляя f в выражение для компоненты, отвечающей за быстрые осцилляции, получаем:

и находим среднеквадратичную скорость этих колебаний.

.

. Таким образом:

.

Условия устойчивости положений равновесия при разных соотношениях параметров модуляции можно сформулировать так:

1. При устойчивое положение ;

2. При устойчивое положение , т.е. во втором случае устойчивому равновесию отвечает значение ненулевого угла .

Случай 3

Т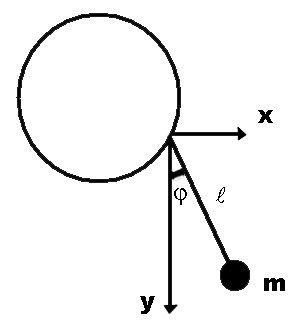 очка подвеса совершает колебания по вертикальной окружности с постоянной частотой.

Запишем уравнения движения маятника относительно осей:

Определим лагранжиан: ; .

Выполним несложные преобразования для вывода формулы кинетической энергии:

Кинетическая энергия: .

Опускаем полную производную по времени ;

Отсюда следует, что .

Подставляем в выражение для кинетической энергии и опускаем все полные производные по времени:

.

Лагранжиан равен: . Учитывая, что , а , где .

Подставляя f в выражение для компоненты, отвечающей за быстрые осцилляции, получаем: и находим среднеквадратичную скорость этих колебаний:

.

Это верно в случае, если вертикальная и горизонтальная компоненты частоты колебания подвеса одинаковы, и амплитуды колебания тоже равны. . Таким образом, для этого случая:

.

Автоматизация вычислений на ПК в задачах теоретической физики и построение поверхностей эффективной потенциальной энергии при движении в быстро осциллирующих полях оказывается весьма полезным инструментом для изучения условий возникновения параметрических колебаний. Трехмерные графики, реализованные в среде компьютерной математики, позволяют исследовать перестройку положений устойчивого равновесия и представить результат в наглядном виде.

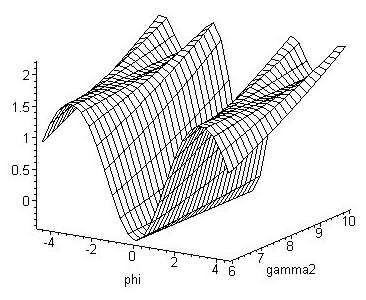
Рис.23. Поверхность эффективной энергии