3. Колебания и адиабатические инварианты

Законы колебательного движения обладают универсальностью, общностью для колебаний различной физической природы. Академик Л.И.Мандельштам отмечал: "Теория колебаний объединяет, обобщает различные области физики... Каждая из областей физики^_ оптика, механика, акустика^_ говорит на своем «национальном» языке. Но есть «интернациональный» язык, и это^_ язык теории ко­лебаний... Изучая одну область, вы получите тем самым интуицию и знания совсем в другой области".

Изменение параметров физической системы всегда сопровождается изменением не­которых характеристик ее движения. Однако в некоторых случаях в физической систе­ме существуют характеристики, которые сохраняются при медленном (адиабатическом) изменении со временем каких-либо параметров системы. Такие величины называются адиабатическими инвариантами. Геометрический смысл инварианта- это площадь замкнутой фазовой траектории.

3.1 Гармонический осциллятор

Из кинематики гармонических колебаний после несложных преобразований следует, что траектория осциллятора в фазовой плоскости (x,v) является эллипсом, размер которого опре­деляется начальными условиями, а площадь его, равная произведению энергии на период является адиабатическим инвариантом ( ).

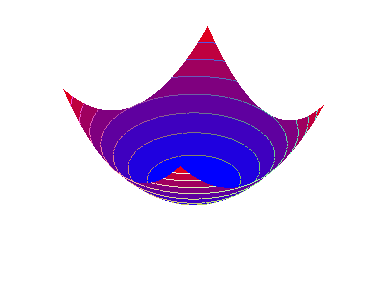
Рис.19. Адиабатический инвариант в трехмерной графике

Указание. Исследовать гамильтониан и фазовые траектории пружинного маятника при малых измене­ниях его жесткости, используя интерактивную компьютерную графику.

Слайд 16. Анимация гармонических колебаний

3.2 Задача «Бездонный колодец»

Предположим, что Земля просверлена по диаметру (рис.20). В образовавшийся колодец опустили небольшой предмет массой m. Определить характер движения тела и скорость в центре Земли без учета сопротивления воздуха. Масса Земли Мз=6 10²⁴ кг, радиус R= 6400 км.

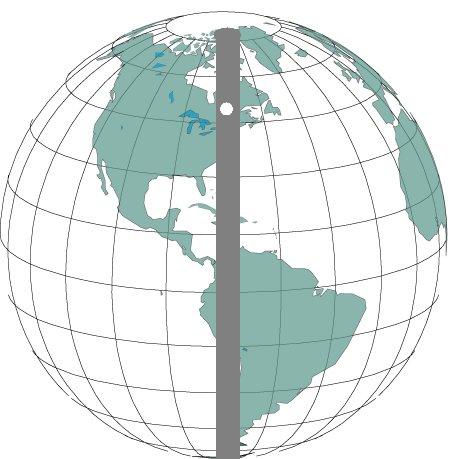
Рис.20 . К задаче «Бездонный колодец»

Взаимодействие с внешним шаровым слоем отсутствует, т.к. его можно разбить на сферы, внутри которых тяготения нет (задача Ньютона). Поэто­му тело взаимодействует только с шаром радиуса «х» с силой , где масса шара- , плотность Земли (ось ОХ направлена по диаметру). Считая ускорение свободного падения на поверхности Земли и пренебрегая сопротивлением воздуха, после несложных преобразований находим дифференциальное уравнение движения , т.е. уравнение гармонических колебаний с периодом [4].

Вращение представляет собой суперпозицию перпендикулярных гармонических колебаний, поэтому полученное решение совпадает с периодом кругового вращения спутника (~ 1,5 час), а скорость в центре Земли совпадает с первой космической скоростью (~8 км/c).

Указание. Рассмотреть проект «Сказочная дорога». Изучить движение тела в тоннеле, соединяющем две противоположные точки на поверхности Земли.

3.3 Фигуры Лиссажу

Демонстрация на экране монитора сложения двух взаимно перпенди­кулярных колебаний с различными амплитудами, частотами и разностями фаз (рис. 21)

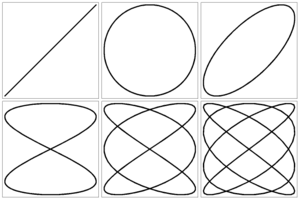
Рис. 21. Сложение колебаний в плоскости

Слайд 17. Фигуры Лиссажу в анимационной графике