3.2.5. Среднее квадратическое отклонение

Если извлечь из дисперсии квадратный корень, получим среднее квадратическое отклонение

.

Размерность величины та же, что и случайной величины Х.

Пример. По распределению

Х	2	3	10
р	0,1	0,4	0,5

требуется вычислить среднее квадратическое отклонение.

Решение.

Среднее квадратическое отклонение суммы взаимно независимых случайных величин равно

Доказательство.

Дисперсия суммы случайных величин равна

.

Тогда

.

3.2.6. Одинаково распределенные взаимно независимые случайные величины

Рассмотрим n взаимно независимых одинаково распределенных случайных величин Х₁,Х₂,…,Х_n.

Для них среднее арифметическое равно

.

Докажем три положения [3]:

1. Математическое ожидание среднего арифметического n взаимно независимых одинаково распределенных случайных величин равно математическому ожиданию а каждой из величин

.

Доказательство:

.

2. Дисперсия среднего арифметического n взаимно независимых одинаково распределенных случайных величин в n раз меньше дисперсии D каждой из величин:

.

Доказательство:

Так как постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, то

.

3. (следует из п.2), т.е. среднее арифметическое n взаимно независимых одинаково распределенных случайных величин имеет значительно меньшее рассеяние (в раз), чем каждая отдельная величина.

3.2.7. Моменты (начальные, центральные) дискретной случайной величины

Начальный момент порядка r – это математическое ожидание случайной величины Х^r

.

Например, начальные моменты первого и второго порядков равны

ν₁=M(X); ν ₂=M(X²).

Центральный момент порядка r задается формулой

,

при этом .

Центральный момент второго порядка представляет собой дисперсию.

Между начальными и центральными моментами существуют соотношения

Следовательно, формула для вычисления дисперсии может быть записана в виде

.

3.3. Примеры законов распределения дискретных случайных величин

3.3.1. Гипергеометрическое распределение

.

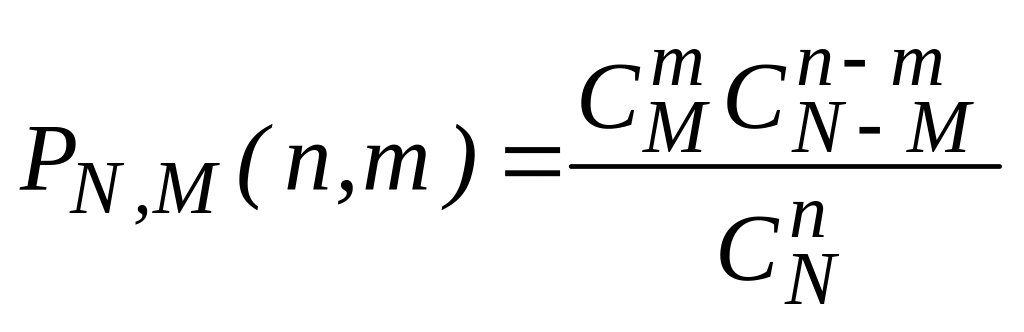В партии из N изделий М стандартных (М<N). Из партии отбирают n изделий (без возврата).

Случайная величина m – число стандартных изделий среди n отобранных имеет гипергеометрическое распределение. Оно широко используется в статистических методах контроля качества продукции.

3.3.2. Биномиальный закон

Если в гипергеометрическом распределении объем партии изделий увеличивать, то гипергеометрическое распределение будет приближаться к биномиальному закону (М/N=р)

.

Здесь выборка – с возвращением!

3.3.3. Закон Пуассона

Следует из биномиального при n→∞ и малой вероятности р (величина np – постоянная)

,

где np – среднее. При и q (или р) ≤ 0,1 закон Пуассона можно использовать вместо гипергеометрического.

IV. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

4.1. Функция распределения

Функцией распределения (интегральной функцией распределения) случайной величины Х называется функция F(х), значения которой равны вероятностям Р(Х<x)

F(x)=P(X<x)=P(–∞<X<x).

Из этого определения вытекают следующие свойства функции распределения:

1. 0F(x)1.

2. F(b)F(а) при b>a, т.е. функция распределения - неубывающая.

3. P(aX<b)=F(b)–F(a).

4. , если распределение задано на всей числовой оси.

5. Если между двумя случайными величинами Х и Y существует функциональная зависимость Y=φ(X), причем, с ростом Х монотонно растет и Y, то их функции распределения равны

F(x)=F(y)=F(φ(x)).

6. Если с ростом Х величина Y монотонно убывает, то

F(x)=1–F(y)=1- F(φ(x)).