5.4. Метод моментов для точечной оценки параметров распределения

Метод предложен английским статистиком К. Пирсоном в конце прошлого века.

Его достоинство – чрезвычайная простота, особенно при небольшом числе параметров. Суть его сводится к приравниванию теоретических моментов, выраженных через параметры распределения, к эмпирическим.

Пусть задана плотность распределения с одним параметром, например, показательный закон

.

Требуется найти методом моментов точечную оценку параметра  по выборке t₁,t₂,…,t_n.

Решение. Выразим математическое ожидание через параметр 

.

Приравняем далее эмпирический и теоретический моменты , откуда .

Оценка двух параметров. Запишем нормальный закон распределения

.

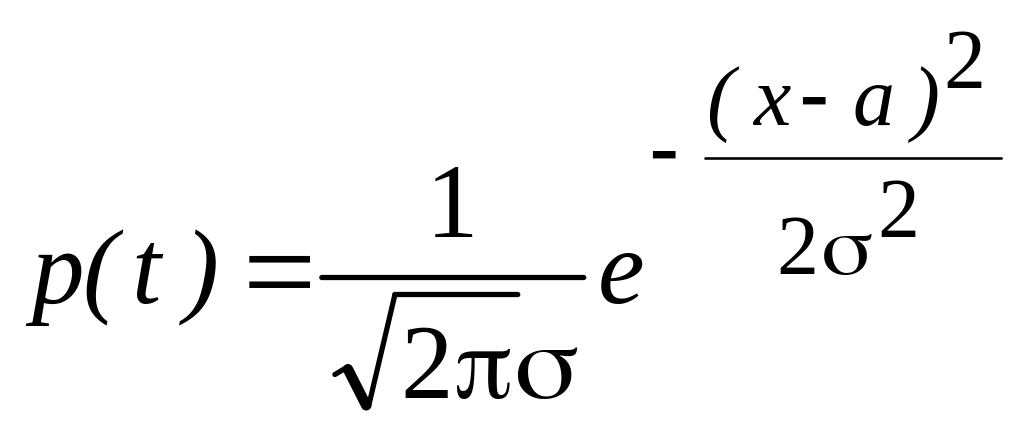Здесь .

По выборке t₁,t₂,…,t_n находим и и приравниваем теоретические моменты эмпирическим.

Следовательно, ; .

При бóльшем числе параметров необходимо составить r уравнений (по числу параметров) с r неизвестными и решить эту систему.

5.5. Метод наибольшего правдоподобия

Метод предложен английским статистиком Р. Фишером в 1912 г.

Обозначим вероятность того, что в результате испытания величина Х примет значение , через (для дискретной величины).

Функцией правдоподобия дискретной случайной величины называют функцию аргумента :

.

В качестве точечной оценки параметра  принимают такое его значение *, при котором функция правдоподобия достигает максимума. Оценку * называют оценкой наибольшего правдоподобия.

Обычно вместо L используют логарифм функции правдоподобия , поскольку обе функции достигают максимума при одном и том же значении .

Оценка  находится из условия .

Оценки метода наибольшего правдоподобия (МНП) не всегда совпадают с оценками метода моментов и часто требуют сложных вычислений.

Пример. Найти для показательного закона оценку параметра  по МНП.

Видоизменим несколько МНП.

В качестве логарифмической функции правдоподобия используем величину .

Для этого вначале логарифмируем плотность р(t):

.

Далее находим математическое ожидание

.

Берем первую производную по α

.

Приравнивая полученное выражение нулю, находим =1/М(t).

Теперь осталось приравнять М(t) среднему выборочному и записать оценку параметра  в виде: .

VI. Обобщенные распределения. Системы непрерывных распределений

В теории вероятностей и математической статистике известно большое количество непрерывных распределений. Однако, как показала практика, они не могут с достаточной точностью описать все многообразие статистических распределений. Кроме того, их использование затруднено тем, что они не сведены в систему.

Сложившаяся в настоящее время в прикладной статистике ситуация сравнима с той, которая была в химии накануне создания «Периодической системы элементов» Д.И. Менделеева – было известно достаточно много элементов, в некоторой степени изучены их свойства, но еще не было главного – «Периодического Закона», позволявшего предсказывать существование еще не открытых элементов и их свойства.

Следовательно, главная задача теории вероятностей и математической статистики на данном этапе – создание своего рода «Периодической системы распределений», исследование их свойств, разработка общих критериев для установления закона распределения случайной величины по статистическому распределению и разработка общих методов оценивания параметров.

Задача построения универсальных вероятностных моделей для аппроксимации (выравнивания) широкого класса статистических распределений в настоящей работе ставится не впервые.

Еще в 1895 г. английский статистик К. Пирсон предложил свое семейство непрерывных распределений, заданное в виде дифференциального уравнения [14, c.129].

.

Это семейство распределений он получил путем выравнивания дискретного гипергеометрического распределения. Им же был предложен метод моментов (назовем его классическим методом моментов) для нахождения оценок параметров выравнивающих распределений.

Существенным недостатком семейства распределений К. Пирсона является отсутствие обобщенной плотности, представленной в явном виде, что сильно ограничивает возможности его использования на практике. Кроме того, метод моментов не позволяет находить оценки параметров тех распределений, в том числе принадлежащих семейству К. Пирсона, которые не имеют моментов высших порядков (3-го или 4-го).

В 1912 г. английский статистик Р. Фишер предложил другой метод оценивания параметров практически любых распределений – метод наибольшего правдоподобия. Однако для использования этого метода необходимо заранее знать тип выравнивающего распределения. Кроме того, он требует совместного решения весьма сложных уравнений правдоподобия, число которых равно числу оцениваемых параметров.

Таким образом, задача установления типа выравнивающей кривой распределения и нахождения оценок параметров к настоящему времени до конца не решена. Поэтому разработка системы непрерывных распределений, более широкой, чем семейство кривых К. Пирсона, а также новых методов оценивания параметров имеет большое значение как в теоретических, так и прикладных исследованиях. Другими словами, требуется создание теории обобщенных распределений. Ниже излагаются элементы этой теории.