VIII. Выравнивание и прогнозирование статистических распределений

8.1. Выбор системы непрерывных распределений для выравнивания статистических распределений

Каждая из трех систем непрерывных распределений предназначена для описания преимущественно своего класса статистических распределений.

Ограничимся рассмотрением двух основных систем непрерывных распределений.

Так, первая система непрерывных распределений в соответствии с ее характерными особенностями наряду с другими должна описывать статистические распределения таких случайных величин, последующие значения которых получаются из предыдущих путем их изменения (сдвига) на всех интервалах на постоянную величину С без изменения частот интервалов. Эти распределения содержат параметры сдвига - , при изменении которых выравнивающая кривая перемещается по горизонтальной оси без изменения формы.

В частном случае, если некоторая случайная величина растет во времени по линейному закону, то ее распределение должно описываться первой системой непрерывных распределений.

Примерами здесь могут служить статистическое распределение работников некоторой организации по возрасту, распределение образцов бетона и других строительных материалов по прочности, распределение технологических погрешностей контролируемых параметров продукции и др.

Аналогично вторая система непрерывных распределений должна описывать статистические распределения таких неотрицательных случайных величин, последующие значения логарифмов которых на всех интервалах получаются из предыдущих путем их изменения (сдвига) на постоянную величину lnC или умножения случайной величины Т на всех интервалах на постоянную С без изменения частот интервалов (при этом ширина интервалов и их границы увеличиваются в С раз).

Если случайная величина растет во времени по показательному закону, то ее распределение должно описываться второй системой непрерывных распределений.

Характерным примером здесь является статистическое распределение работников по заработной плате, а также распределение наработки до отказа, распределение биений и др.

8.2. Построение выравнивающей кривой распределения по статистическим данным

8.2.1. Выравнивание по классическому методу моментов

Рассмотрим примеры на выравнивание статистических распределений обобщенными плотностями.

В табл. 8.2.1 приведена группировка колхозов и совхозов Республики Беларусь по урожайности основных сельскохозяйственных культур в 1992 г. по данным Госкомстата Республики Беларусь: а) зерновые и зернобобовые культуры; б) картофель.

К сожалению, группировка выполнена не совсем корректно: для анализа табличных данных желательна разбивка на интервалы равной ширины, причем не должно быть открытых интервалов, таких, как до 15ц/га, более 55 ц/га.

Пример 1.

Рассмотрим статистическое распределение хозяйств Минской области по урожайности зерновых и зернобобовых культур в 1992 г. (см. табл. 8.2.2, графы 1 – 3).

Табл. 8.2.1

Группировка колхозов и совхозов Республики Беларусь

по урожайности основных сельскохозяйственных культур в 1992 г.

а) Зерновые и зернобобовые культуры

Сбор с 1 га ц	РБ	Число хозяйств по областям
		Брестская	Витебская	Гомельская	Гродненская	Минская	Могилевская
до 15 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55 >55	139 305 446 639 489 282 117 48 10 5	- 3 24 78 105 78 40 21 5 4	122 186 97 72 18 6 2 1 - -	- 26 73 137 90 60 27 10 3 1	5 11 58 101 72 30 12 3 - -	10 64 129 136 115 45 15 3 1 -	2 15 65 115 89 63 21 10 1 -
Итого:	2480	358	504	427	292	518	381

б) Картофель

Сбор с 1 га ц	РБ	Число хозяйств по областям
		Брестская	Витебская	Гомельская	Гродненская	Минская	Могилевская
до 50 50-75 75-100 100-125 125-150 150-175 175-200 200-225 225-250 250-300 >300	391 480 483 433 271 156 79 48 21 12 2	6 34 45 80 60 46 31 19 7 8 2	211 109 63 36 16 14 5 1 2 1 -	34 60 96 102 59 33 14 13 6 2 -	2 19 57 85 67 28 14 6 1 1 -	97 163 131 68 29 12 5 2 2 - -	41 95 91 62 40 23 10 7 3 - -
Итого:	2376	338	458	419	280	509	372

Табл. 8.2.2

Распределение колхозов и совхозов Минской области

по урожайности зерновых и зернобобовых культур в 1992 г.

Сбор с 1 га ц.	Середина интерв. ti	Число хозяйств		Теорет. плотность p(ti)	Теорет. частота mi=p(ti)Mh
5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55	7,5 12,5 17,5 22,5 27,5 32,5 37,5 42,5 47,5 52,5	- 10 64 129 136 115 45 15		0,00009 0,00410 0,02347 0,04984 0,05641 0,03978 0,01875 0,00604 0,00132 0,00019	60,79 129,09 146,10 103,03 48,56 15,64		0,067 0,170 0,000 0,698 1,391 0,261 0,026 0,002

Требуется: используя классический метод моментов, найти выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить степень близости выравнивающей кривой к статистическому распределению.

Решение. Вычислим по данным табл. 8.2.2. среднюю урожайность, дисперсию, центральные моменты 3-го и 4-го порядков и некоторые другие показатели.

Так как данные сгруппированы (в 9 интервалов равной ширины h=5), то моменты вычисляем по формулам

.

В результате найдем

.

Тогда среднее квадратическое отклонение S и коэффициент вариации V будут равны:

.

Приравнивая эмпирические моменты соответствующим теоретическим, вычислим показатели асимметрии и островершинности, а также критерий L

.

По рис. 7.3.1 находим, что выравнивающее распределение относится к I типу с параметром β = 1, поскольку L<3. В этом случае оценки параметров находятся по формулам (7.3.6):

где величины А,…,Е выражены через показатели и центральные моменты с помощью формул (7.3.8):

Подставляя в последние формулы оценки показателей и соответствующих центральных моментов, получим

А=–0,343314; В=12,17618; С=546,0952; Е=1,872575.

Решим далее квадратное уравнение Аа²+Ва+С=0.

Корни его равны:

а₁=–25,91447; а₂=61,38106.

Для одного из корней должно выполняться равенство а=–₁ (хотя бы в первом приближении). Поэтому параметр а здесь равен (при )

а = –25,91447.

Тогда D = 2C + aB = 776,6512.

Теперь можно рассчитать оценки параметров по формулам (7.3.6):

.

Нормирующий множитель N равен

.

Выравнивающее распределение задается формулой (7.3.41)

,

где

Подставляя сюда оценки параметров и нормирующего множителя N, рассчитаем в серединах каждого интервала значения плотности вероятностей (см. табл. 8.2.2. графа 4).

Все приведенные здесь расчеты выполнялись по программе SNR1MM97.

Оценки параметров u, , можно найти по номограмме (Приложение 2). При заданных значениях с учетом неравенства имеем: u = 0,10; k = 25. Тогда u = 1/k = 0,04; k = 1/u = 10.

Эти оценки близки к найденным оценкам по программе.

Оценим далее степень близости выравнивающей кривой к статистическому распределению по критерию «xu-квадрат» К. Пирсона:

,

где n – число интервалов.

Умножим значения плотности на величину . Получим теоретические частоты в каждом интервале (графа 5).

Объединим два последних интервала в один, что рекомендуется делать при частоте m_i < 5, и вычислим для каждого интервала (всего 8 интервалов) значения величин (графа 6). При этом теоретическая частота первого интервала (0,23) добавлена к частоте второго интервала.

Критерий оказался равным 2,615. По таблице квантилей - распределения (Приложение 4) при уровне значимости α = 0,05 и числе степеней свободы r=8–4–1=3 (8 – число интервалов статистического распределения, 4 – число параметров выравнивающего распределения) найдем критическое значение . Оно равно 7,815. Поскольку , то нет оснований для отклонения гипотезы о том, что закон распределения хозяйств Минской области по урожайности зерновых и зернобобовых культур в 1992 г. относится к распределению I типа (бета-распределению) с найденными оценками параметров.

По таблице - распределения (Приложение 4) при известном числе степеней свободы (r = 3) и = 2,615 можно также найти вероятность Р( ). В данном случае она равна 0,462. Это значит, что наблюденное расхождение могло появиться за счет случайных причин с вероятностью 0,462.

Поскольку эта вероятность достаточно высокая, т.е. значительно больше обычно принимаемого критерия значимости α = 0,05, то нет оснований отвергать принятую гипотезу о выравнивающем распределении.

Теперь можно построить гистограмму и кривую распределения. Для построения гистограммы необходимо вычислить эмпирическую плотность в каждом интервале. Она рассчитывается по формуле

,

где - число хозяйств в i-ом интервале; h – ширина интервала.

Кривая распределения строится по значениям теоретической плотности в серединах интервалов.

Результаты представлены на рис. 8.2.1. На графике отмечена средняя урожайность ц/га, а также нижняя t_н = 16,65 и верхняя t_в=39,22 90%-ные границы.

Это значит, что 90% хозяйств имели урожайность зерновых и зернобобовых на интервале t_н<t<t_в.

Дальнейшие расчеты показывают, что из семи статистических распределений, заданных таблицей 8.2.1а, только одно (Гродненская область) описывается обобщенной плотностью

при u<0, т.е. кривой III типа. Остальные шесть распределений описываются плотностью (7.3.41)

с параметром u > 0, т.е. кривыми I типа. Это – известные бета-распределения.

Р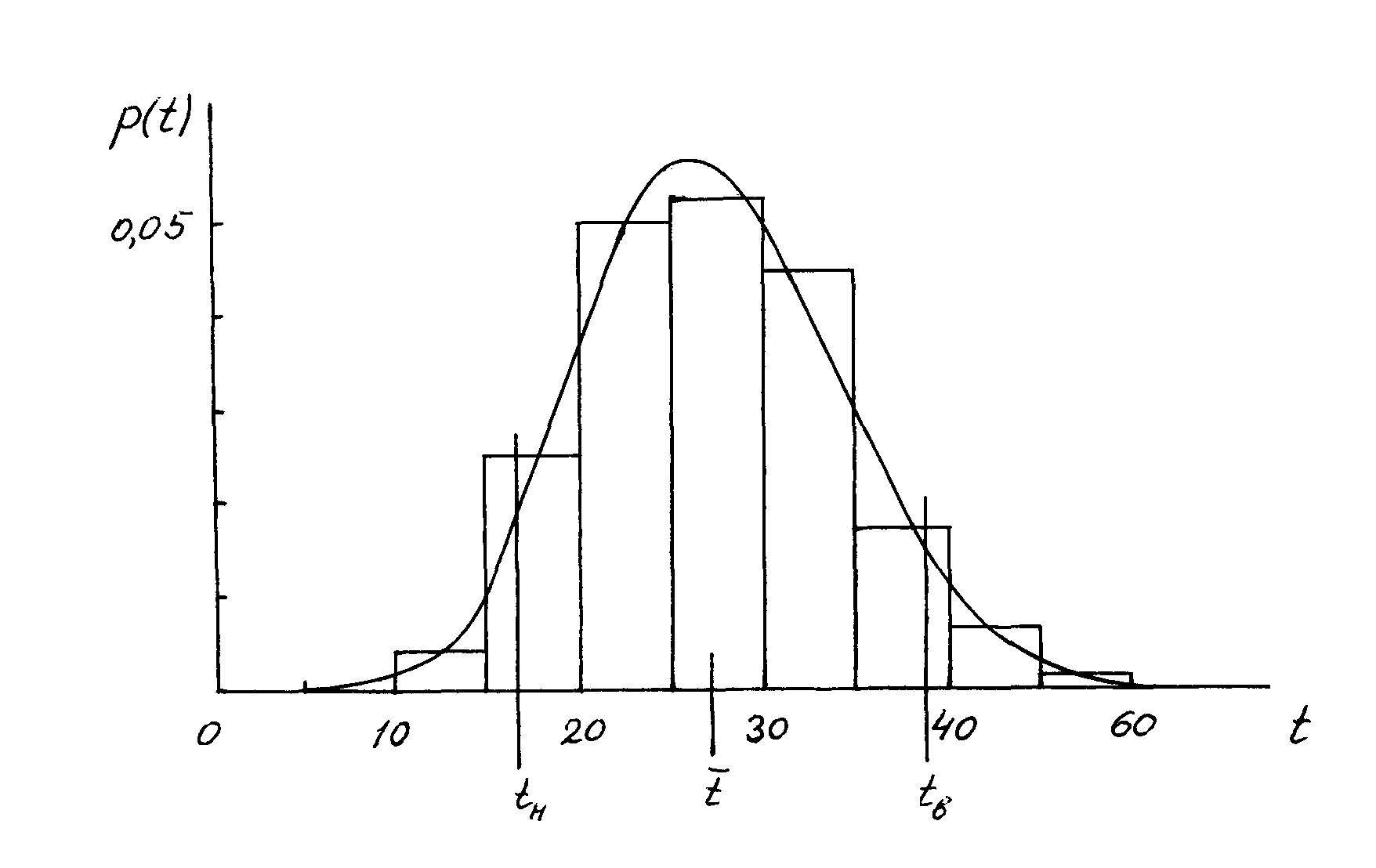 ис. 8.2.1. Распределение колхозов и совхозов Минской области по урожайности зерновых и зернобобовых культур в 1992 г.

Кривые распределения несколько различаются как по расположению на горизонтальной оси, так и по форме. Так, кривая распределения хозяйств Брестской области по урожайности зерновых и зернобобовых культур смещена вправо относительно аналогичной кривой для Республики в целом, а кривая по Витебской области – влево. Последняя кривая отличается сильной правосторонней асимметрией. Такая форма кривой может свидетельствовать о том, что меньшая урожайность уже вряд ли возможна, а также о наличии резервов повышения урожайности либо о неблагоприятных климатических и других условиях для данной культуры.

Пример 2

Табл. 8.2.3

Интервальный ряд распределения предела прочности на растяжение портландцементного раствора 28-дневного возраста [8, c.269]

Интервал в кг/см2	Середина интерв. ti	Эмпирическая частота	Теорет. плотность p(ti)	Теорет. частота mi=p(ti)Mh
15,5-16,5 16,5-17,5 17,5-18,5 18,5-19,5 19,5-20,5 20,5-21,5 21,5-22,5 22,5-23,5 23,5-24,5 24,5-25,5 25,5-26,5 26,5-27,5	16 17 18 19 20 21 22 23 24 25 26 27	74 138 194 202 156 104 62 27	0,00404 0,02713 0,07837 0,14217 0,18810 0,19449 0,16208 0,10966 0,05952 0,02506 0,00766 0,00151	78,37 142,17 188,10 194,49 162,08 109,66 59,52 25,06	0,26 0,24 0,12 0,19 0,29 0,23 0,29 0,10 0,15 0

Требуется: по данным табл. 8.2.3 (графы 1 – 3) найти по классическому методу моментов выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить степень близости выравнивающей кривой к статистическому распределению. Найти границы доверительного интервала при заданной доверительной вероятности Р = 0,9545.

Решение. Вычислим по статистическим данным с помощью программы SNR1MM97 среднее значение предела прочности, дисперсию, центральные моменты 3 и 4-го порядков и другие показатели.

В результате найдем:

.

Среднее квадратическое отклонение S и коэффициент вариации V равны:

.

Приравнивая эмпирические моменты соответствующим теоретическим, вычислим показатели асимметрии и островершинности, а также критерий L

.

Поскольку L < 3, выравнивающее распределение относится к I типу с параметром =1 и задается плотностью

.

Вычислим значения величин А,…,Е:

Решим далее квадратное уравнение Аа²+Ва+С=0. Корни его равны: а₁ = –6,59544; а₂ = 9,824492.

Поскольку , то параметр а здесь равен а = –6,59544.

Тогда D=2С+аВ=68,35499.

Теперь можно рассчитать оценки параметров:

Нормирующий множитель N = 5,314906·10^–4.

Кривая распределения задана на интервале 14,27656<t<30,69649.

Рассчитаем при найденных оценках параметров и нормирующего множителя N значения плотности вероятностей (см. табл. 8.2.3, графа 4). Умножив значения плотности на М·h = 1000, получим теоретические частоты в каждом интервале (графа 5).

Вычислим критерий «xu-квадрат» К. Пирсона. Объединив частоты двух первых и двух последних интервалов, получим . Далее по таблице – распределения при числе степеней свободы (число интервалов после объединения стало равным 10; 4 – количество параметров обобщенного распределения) и найдем вероятность того, что за счет случайных причин мера расхождения между статистическим и выравнивающим распределениями будет не менее 1,87. Эта вероятность достаточно высокая – . Это значит, что нет оснований для отклонения принятой гипотезы о выравнивающем распределении.

Вычислим по Программе нижнюю и верхнюю границы доверительного интервала при доверительной вероятности Р = 0.9545: t_н = 17,25485; t_в=24,88674. При этом значение функции распределения F(t_н)=0,02275; F(t_в)=0,97725. Ширина доверительного интервала равна 7,63189 кг/см² и составляет 3,92874 средних квадратических отклонений.