3.2. Числовые характеристики дискретной случайной величины

3.2.1. Математическое ожидание

Математическое ожидание дискретной случайной величины равно сумме произведений всех ее возможных значений на их вероятности

.

Математическое ожидание есть неслучайная (постоянная) величина.

Пример 1. Найти математическое ожидание случайной величины Х по ее закону распределения:

Х	3	5	2
р	0,1	0,6	0,3

Решение. .

Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.

Решение. Случайная величина Х – число появлений события А в одном испытании – может принимать два значения: х₁ =1 (событие наступило) с вероятностью р и х₂ = 0 (событие не наступило) с вероятностью 1–р=q.

Следовательно,

,

т.е. математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Оценкой математического ожидания является среднее арифметическое наблюденных значений случайной величины.

3.2.2. Свойства математического ожидания

Приведем без доказательства основные свойства математического ожидания.

1. М(С)=С – математическое ожидание постоянной величины С равно значению самой постоянной.

2. М(СХ)=СМ(Х) – постоянную величину можно выносить за знак математического ожидания.

3. М(ХY)=М(Х)М(Y) – для двух независимых случайных величин математическое ожидание произведения равно произведению их математических ожиданий.

4. М(Х+Y)=M(X)+M(Y) – для двух случайных величин (зависимых или независимых) математическое ожидание суммы равно сумме математических ожиданий слагаемых.

Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний n на вероятность появления события в каждом испытании р, т.е.

М(Х)=nр.

Доказательство свойств математического ожидания см., например, в учебниках [2,3].

3.2.3. Дисперсия дискретной случайной величины

Две случайные величины могут иметь одинаковые математические ожидания, но разное рассеяние. Это значит, что математическое ожидание полностью случайную величину не характеризует. Поэтому вводится еще одна числовая характеристика, которая называется дисперсией и характеризует рассеяние случайной величины относительно математического ожидания.

Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания

.

Пример. Случайная величина Х имеет распределение

Х	1	2	5
р	0,3	0,5	0,2

Требуется вычислить дисперсию.

Имеем:

.

На практике для вычисления дисперсии используют другую, более удобную формулу

.

Доказательство:

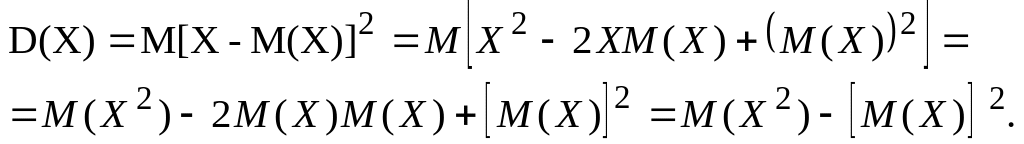
3.2.4. Свойства дисперсии

1. D(С)=0, т.е. дисперсия постоянной величины С равна нулю.

2. D(CX)=C²D(X) – постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат.

Доказательство:

.

3. D(X+Y)=D(X)+D(Y) – дисперсия суммы двух случайных величин равна сумме их дисперсий.

Доказательство:

Так как M(XY)=M(X)M(Y), то последнее равенство примет вид

,

откуда

.

Приведем без доказательства еще два свойства дисперсии.

4. D(C+X)=D(X).

5. D(X–Y)=D(X)+D(Y).

Отметим еще одно важное свойство дисперсии.

Дисперсия числа появлений события А в n независимых испытаниях равна

D(X)=npq.

Доказательство:

Найдем дисперсию числа появлений события А в одном испытании

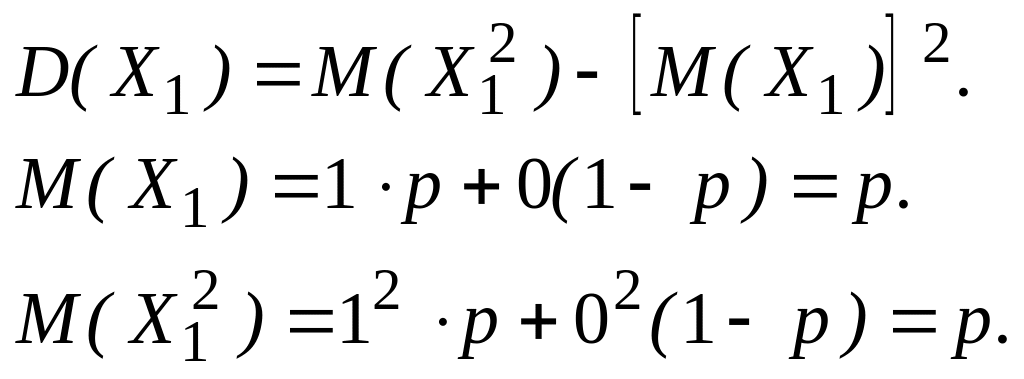
Тогда .

Всего n испытаний, следовательно, D(X)=npq.

Дисперсия имеет размерность случайность величины в квадрате.