
- •Молекулярна фізика. Лабораторний практикум
- •Перелік лабораторних робіт
- •Список рекомендованої літератури
- •Частина і. Молекулярна фізика. Розділ 1. Будова речовини
- •1.1. Модель речовини. Маси атомів і молекул
- •1.2. Сили міжмолекулярної взаємодії. Агрегатні стани речовини
- •1.3. Енергія міжмолекулярної взаємодії. Потенціал Ленарда–Джонса
- •1.4. Структура речовини
- •1.4.1. Газоподібний стан
- •1.4.2. Рідини
- •1.4.3. Тверді тіла
- •Розділ 2. Основи молекулярно-кінетичної теорії газів
- •2.1. Ідеальний газ. Ізопроцеси. Рівняння стану ідеального газу
- •2.2. Тиск і температура ідеального газу. Основне рівняння молекулярно-кінетичної теорії
- •2.3. Поняття про статистичний розподіл. Функції розподілу
- •2.3.1. Закони розподілу молекул ідеального газу за швидкостями й енергіями теплового руху (розподіл Максвелла)
- •2.3.2. Барометрична формула. Розподіл Больцмана
- •2.3.3. Розподіл Максвелла–Больцмана
- •2.3.4. Квантові аспекти розподілів. Розподіли Бозе–Айнштайна і Фермі–Дірака
- •2.4. Середня кількість зіткнень молекул. Середня довжина вільного пробігу
- •Розділ 3. Основи термодинаміки
- •3.1. Головні поняття й означення
- •3.2. Внутрішня енергія ідеального газу Молекули ідеального газу не взаємодіють на відстані, тому
- •Вище доведено, що середня кінетична енергія теплового руху молекули ідеального газу
- •3.3. Теплоємність ідеального газу
- •Для ізобарного процесу
- •3.4. Теплоємність рідин
- •3.5. Теплоємність твердих тіл
- •3.5.1. Класична теорія теплоємності твердих тіл
- •3.5.2. Квантові теорії теплоємності твердих тіл.
- •3.6. Адіабатний процес
- •3.7. Політропні процеси
- •3.8. Робота в термодинамічних процесах
- •3.9. Стисливість газів
- •3.10. Ентропія
- •3.11. Циклічні процеси. Теплові машини
- •Розділ 4. Реальні гази
- •4.1. Рівняння стану реального газу. Рівняння Ван-дер-Ваальса
- •4.2. Внутрішня енергія і теплоємність реального газу
- •Розділ 5. Поверхневий натяг. Капілярні явища
- •На підставі (5.3) рівняння (5.4) запишемо у вигляді
- •Розділ 6. Фазові переходи
- •6.1. Агрегатні стани і фази речовини
- •6.2. Фазові переходи першого і другого роду
- •Розділ 7. Явища перенесення
- •7.1. Самодифузія і взаємна дифузія
- •7.2. Теплопровідність
- •7.4. Розріджені гази. Вакуум
- •Частина іі. Молекулярна фізика. Лабораторний практикум. Лабораторна робота № 201. Визначення коефіцієнта в’язкості рідини методом стокса
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 202. Дослідження залежності коефіцієнта в’язкості рідини від температури
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 203. Визначення коефіцієнта в’язкості рідини за допомогою капілярного віскозиметра оствальда
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №205. Визначення коефіцієнта поверхневого натягу рідини методом відривання кільця
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 206. Дослідження залежності коефіцієнта поверхневого натягу рідини від температури методом максимального тиску в бульбашці
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №208. Дослідження теплового розширення металів
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №209. Визначення питомої теплоємності металів методом охолодження
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 210. Визначення сталої больцмана та універсальної газової сталої
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №211. Визначення середньої довжини вільного пробігу та ефективного діаметра молекул повітря
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 212 визначення співвідношення теплоємностей повітря сp/сv методом клемана–дезорма
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 213. Визначення співвідношення теплоємностей повітря ср / сv методом стоячої хвилі
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 214. Вимірювання вологості повітря психрометром
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 215. Дослідження критичного стану речовини
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №216. Дослідження процесу плавлення кристалічних речовин
- •Порядок виконання роботи
- •Контрольні запитання
- •Додатки Головні фізичні сталі
- •Густина твердих тіл . За температури 20ºС
- •Густина рідин за температури 20ºС
- •Густина газів
- •Додаток 4 Теплофізичні коефіцієнти твердих тіл
- •Додаток 5 Пружні властивості твердих тіл
- •Додаток 6 Коефіцієнти лінійного теплового розширення твердих тіл в інтервалі 0–100 ºС
- •Додаток 7 Швидкість поширення звуку в різних середовищах
- •Додаток 8 Деякі фізичні характеристики рідин
- •Додаток 11 Коефіцієнт об’ємного теплового розширення деяких рідин
Розділ 7. Явища перенесення
У
Рис. 7.1. Потік J
через поверхню S
Розглянемо
детальніше процес перенесення в газі
деякої фізичної величини А у напрямі
осі Ох потоком J молекул у
середовищі зі сталим градієнтом
![]() (рис. 7.1).
(рис. 7.1).
Молекули в потоці J перетинають площину S на відстані середньої довжини вільного пробігу l. Це достатньо мала величина, тому А в околі точки х можна виразити у вигляді
![]() =A(x)
=A(x)![]() (7.1)
(7.1)
обмежившись першим членом розкладу в ряд Тейлора.
Кількість молекул,
які перетинають площу S за час t,
рухаючись в додатному напрямку осі Ох,
дорівнює
![]() .
Потік J величини А уведемо як
.
Потік J величини А уведемо як
![]() .
(7.2)
.
(7.2)
Зазначимо, що в газі існуватимуть два взаємно протилежні потоки вздовж Ох:
![]() ;
(7.3)
;
(7.3)
![]() .
(7.4)
.
(7.4)
Підсумковий потік у додатному напрямі Ох:
![]() .
(7.5)
.
(7.5)
Рівняння (7.5) – це основне рівняння явищ перенесення.
7.1. Самодифузія і взаємна дифузія
Самодифузія – це явище перенесення в однорідному газі з односортних молекул за наявності градієнта концентрації n. Під час самодифузії величиною А, яка зазнає перенесення, є концентрація n, а саме А= n/n0, де n0 – рівноважна концентрація молекул у газі. Тоді на підставі (7.5) отримаємо рівняння Фіка для самодифузії
 ,
(7.6)
,
(7.6)
де
![]() – коефіцієнт дифузії.
– коефіцієнт дифузії.
Якщо газове
середовище містить два сорти молекул,
які відрізняються між собою властивостями,
то за умови р=const, T=const у газі
простежуватиметься взаємна дифузія,
під час якої виникнуть три молекулярні
потоки: два дифузійні
![]() ,
,
![]() і один гідродинамічний
і один гідродинамічний
![]() де
де
![]() ,
,
![]() і D1D2.
і D1D2.
Гідродинамічний потік – це рух газу як цілого, зумовлений необхідністю підтримувати тиск газу сталим у всьому об’ємі. Тоді
![]()
За цих умов коефіцієнт взаємної дифузії для суміші газів
 (7.7)
(7.7)
Формула (7.7) дещо незручна, оскільки потребує громіздких попередніх обчислень довжин вільного пробігу молекул, тому Дж. Максвел і Ц. Стефан для моделі молекул як твердих куль запропонували спрощений метод розрахунку D12, згідно з яким
 ,
(7.8)
,
(7.8)
де
![]() – середній радіус молекул суміші.
– середній радіус молекул суміші.
7.2. Теплопровідність
Явище перенесення енергії теплового руху молекул у середовищі за наявності градієнта температури називають теплопровідністю. За цих умов величиною А, яка зазнає перенесення, є теплота q, що припадає на одну молекулу. Для ідеального газу, згідно з теоремою Больцмана про рівноймовірність розподілу енергії молекули за ступенями вільності,
 (7.9)
(7.9)
Отже, у рівнянні перенесення (7.5) А=q. Тоді потік теплоти
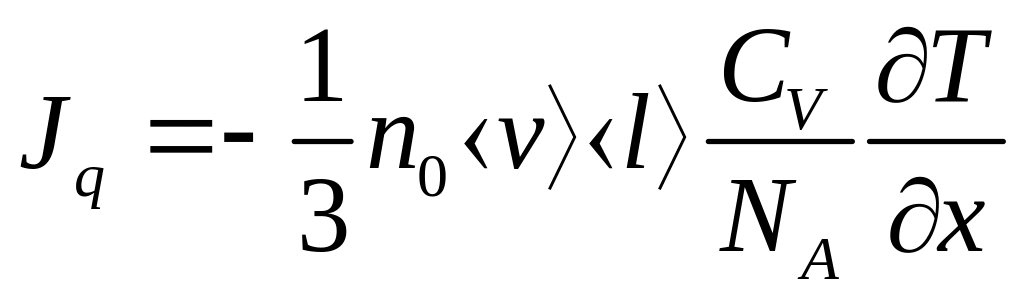 ,
(7.10)
,
(7.10)
або ![]() (7.11)
(7.11)
де
![]() – густина газу,
– густина газу,
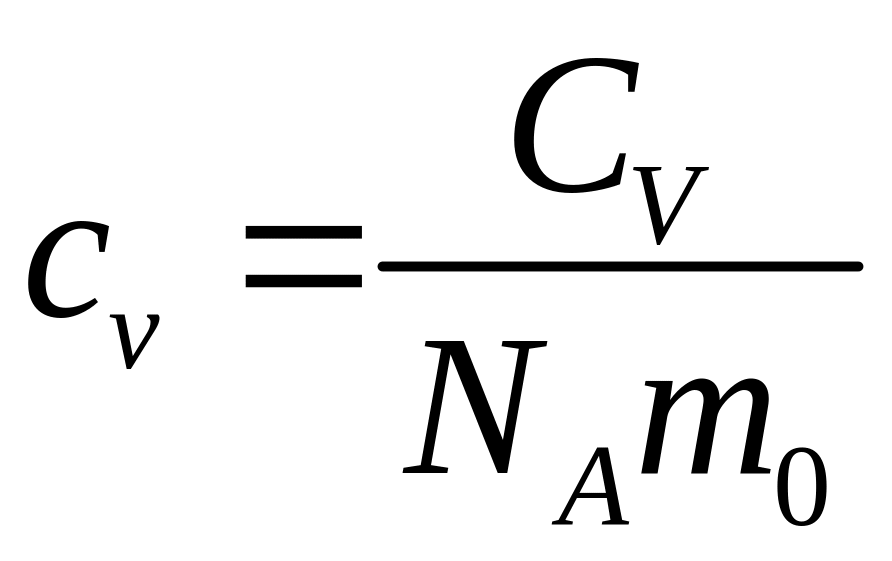 – питома теплоємність газу за сталого
об’єму,
– питома теплоємність газу за сталого
об’єму,
![]() – коефіцієнт теплопровідності.
– коефіцієнт теплопровідності.
Рівняння (7.11) – це рівняння Фур’є для теплопровідності.
Коефіцієнт
теплопровідності газів не залежить від
тиску, однак збільшується з підвищенням
температури, оскільки
![]() .
.
7.3. В’язкість
В
Рис. 7.2. Виникнення градієнта швидкості
у потоці в’язкої рідини
Отже, між шарами виникає градієнт швидкості, спрямований перпендикулярно до напряму потоку. Обмін молекулами між шарами спричинює гальмування швидшого шару і пришвидшення повільного. В цьому полягає механізм виникнення внутрішнього тертя у газі. Величиною, що переноситься у цьому випадку, є імпульс молекули А=mv. За таких умов рівняння перенесення (7.5) набуває вигляду
![]() (7.12)
(7.12)
Це рівняння
Ньютона для внутрішнього тертя. Тут
![]() – коефіцієнт динамічної в’язкості
газу.
– коефіцієнт динамічної в’язкості
газу.
Подібно до коефіцієнта теплопровідності коефіцієнт в’язкості газів не залежить від тиску і збільшується з підвищенням температури ( ). Поряд з коефіцієнтом динамічної в’язкості на практиці використовують і коефіцієнт кінематичної в’язкості
![]() .
(7.13)
.
(7.13)
Подібність законів перенесення у газах (7.6), (7.11), (7.12) зумовлена спільним для цих явищ механізмом перемішування молекул газу внаслідок їхнього хаотичного руху і взаємодії. Якщо порівняти отримані вирази для коефіцієнтів перенесення, то неважко виявити взаємозв’язок між ними:
![]() ,
,
![]() ,
,
![]() .
(7.14)
.
(7.14)
Ми розглянули
явища перенесення, коли градієнт величини
А є сталим. Однак часто потрібно
описати ці явища за умови, коли
![]() .
Наприклад, якщо ізольовану термодинамічну
систему, що перебуває у нерівноважному
стані, залишити саму на себе, то з часом
вона перейде до рівноважного стану. За
цих умов у середовищі відбувається
вирівнювання температур або концентрацій
газу в усіх просторових точках об’єму,
в якому міститься газ. Це нестаціонарні
явища перенесення, які описують дещо
іншими співвідношеннями, ніж (7.6), (7.11),
(7.12). Зокрема, рівняння нестаціонарної
теплопровідності в ізотропному
однорідному середовищі
.
Наприклад, якщо ізольовану термодинамічну
систему, що перебуває у нерівноважному
стані, залишити саму на себе, то з часом
вона перейде до рівноважного стану. За
цих умов у середовищі відбувається
вирівнювання температур або концентрацій
газу в усіх просторових точках об’єму,
в якому міститься газ. Це нестаціонарні
явища перенесення, які описують дещо
іншими співвідношеннями, ніж (7.6), (7.11),
(7.12). Зокрема, рівняння нестаціонарної
теплопровідності в ізотропному
однорідному середовищі
![]() ,
(7.15)
,
(7.15)
де
 – температуропроводність
середовища;
– температуропроводність
середовища;
![]() – оператор Лапласа.
– оператор Лапласа.
Рівняння нестаціонарної дифузії в ізотропному однорідному середовищі
![]() ,
(7.16)
,
(7.16)
де Cp – питома теплоємність середовища за сталого тиску; – оператор Лапласа.
