2.6. Прямокутна система координат Гаусса-Крюгера

Довгий час людство шукало простішу систему координат, ніж географічна, для визначення положення точки, яка закріплена на фізичній поверхні Землі. В 1637 р. французький математик Р. Декарт опублікував свою книгу ''Геометрія'', в якій приведена структура системи прямокутних координат. Дану систему називають декартовою системою координат (рис. 17).

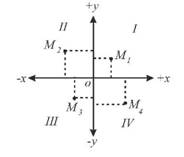
Рис.17. Система прямокутних координат В математиці прийнято за вісь x горизонтальну лінію, а за вісь у вертикальну лінію, які перетинаються під прямим кутом. Точку перетину осей приймають за нуль. Таким чином створено чотири четверті і їх рахунок ведуть проти годинникової стрілки, починаючи від позитивного кінця осі X.

Дана система прямокутних координат може доцільно використовуватися на порівняно малих ділянках місцевості, коли їх приймають за площину. Це буде своя місцева система координат. Координати точок, які обчислені відносно різних їх початків, тобто в різних системах не можуть бути використані для складання точних планів і топографічних карт на великі ділянки, якщо попередньо не встановити зв'язок між цими системами. Якщо питання стоїть про великі ділянки місцевості або всієї земної кулі, то зручно використати одну загальну систему координат. Тут постає питання, як врахувати кривизну земної поверхні?

Теорію прямокутних координат для визначення положення точок на земній поверхні розробив в 1825 - 1830 рр. відомий німецький вчений - геодезист К. Гаусс. Методику практичного використання цієї теорії розробив і запропонував німецький геодезист Л. Крюгер в 1912 р. Ось чому дану систему координат називають системою координат Гаусса - Крюгера.

Суть даної системи прямокутних координат Гаусса - Крюгера полягає в наступному. Поверхню еліпсоїда ділять на частини шляхом проведенням меридіанів через 6° починаючи з початкового меридіану, який проходить через обсерваторію м. Грінвіча. Перша зона обмежена меридіанами 0° і 6°, друга - 6°-12° і т.д., тобто рахунок виконують із заходу на схід. Таких зон на земній кулі буде 60.

Щоб отримати плоске зображення зони, то необхідно уявити, що земну кулю розмістили в циліндр необхідної величини та на внутрішню його поверхню проектують зони розгорнуті на площині, а після цього розрізають за твірною циліндр і розгортають його на площині (рис.18).

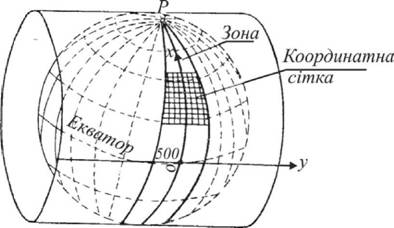
Рис. 18. Проекція на поверхню циліндра

Після цього відбитки зон на площині будуть мати вигляд приведений на рис.19.

Якщо з'єднати північний і південний полюси в кожній зоні, то ми отримаємо їх осьові меридіани, які будуть перпендикулярні до лінії екватору Ці лінії приймають за осі плоских прямокутних координат в системі Гаусса - Крюгера.

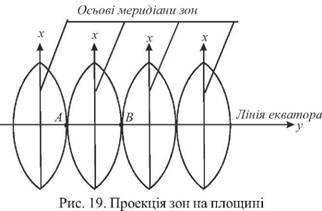
Осьовий меридіан приймають за вісь абсцис і позначають буквою X, лінію екватора приймають за вісь ординат і позначають буквою у. За початок координат приймають точку перетину осей і позначають буквою 0. Таким чином в кожній зоні буде своя система прямокутних координат. Координати абсцис точок відраховуються від їх початку до північного і південного полюсів та можуть змінюватися до 10 000 км. На північ від екватора вони додатні, а на південь - від'ємні. Ординати у відраховуються від осьового меридіану вправо (на схід) і мають додатній знак та вліво (на захід) - від'ємний знак.

Територія нашої держави розташована в північній частині земної кулі, а тому абсциси будуть додатними. Для того, щоб ординати кожної зони були теж додатними, то початок ординати приймають за 500 км. Тобто, перетин абсцис і ординат в кожній зоні прийняті (x=0; у=500 км).

Відомо, що точка земної поверхні може займати положення як на заході зони від осьового меридіану, так і на сході. Ширина зони між точками А і В за лінією екватора дорівнює 670 км, а довжина меридіану зони від південного полюсу до північного становить 20 000 км (рис. 19). Тоді довжина меридіану від екватору до будь-якого полюса становить 10 000 км. В градусній мірі південна чи північна півкулі становлять 90°. Дуга меридіану в 1° становить в середньому 10 000 км : 90 =111,1 км. На цій основі дуга меридіану в 1' становить 111,1 км : 60 = 1850 м, а дуга в 1" становить 31 м.

Найбільш віддалена точка на екваторі від осьового меридіану зони до її границі становить 3°, або у=111,1 км х 3 = 333,3 км. Таким чином ордината у зони може бути найменшою 500 км - 333,3 км=166,7 км, або найбільшою 500 км + 333,3 км = 833,3 км (рис. 20). Такі ординати називаються перетвореними.

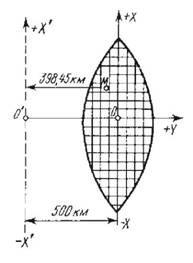
Рис.20. Зональна система координат

На практиці може трапитися так, що точки розташовані на одній лінії паралельної екватору і на однаковій віддалі від осьових меридіанів зон. Це говорить про те, що ординати будуть однаковими для цих точок. Для того, щоб кожна точка земної поверхні мала тільки свою адресу, то перед дійсною ординатою будь-якої точки приписують номер зони. Наприклад, y = 9612,00 км. Це свідчить

п-U

про те, що точка знаходиться в 9 зоні і на сході від осьового

меридіану. Точка M земної поверхні має прямокутні координати xM = 6083,00 км;yM = 17 357,00 км. За даними прямокутних координат точка характеризується наступним чином. Точка M знаходиться в

північній півкулі на віддалі 6083 км від лінії екватора, в 17 U зоні і

на захід від осьового меридіану

Сітка прямокутних координат нанесена на всіх топографічних картах. Горизонтальні лінії сітки проведені паралельно лінії екватора, а вертикальні - паралельно осьовому меридіану зони.

Дану сітку ще називають кілометровою тому, що вона проведена через ціле число кілометрів. Для кожного масштабу топографічних карт прийняті свої розміри сторін квадратів кілометрових сіток.

Коли постає питання визначення прямокутних координат точки K на топографічній карті, то це виконують наступним чином (рис.21).

Виписують координати в кілометрах нижнього лівого кута квадрату в якому знаходиться точка K і перетворюють в метри та додають до них відповідно Ax і Ay в метрах.

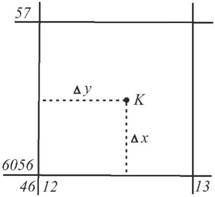
Рис. 21. Визначення прямокутних координат точки K на карті

Нехай Ax=247м і Ay = 844 м, тоді повні прямокутні координати токи будуть xk= 6056247 м; yk =4612844 м. Цифри перед тризначним числом кілометрів ординати відповідають номеру зони, тому число кілометрів в кожній зоні не буває більше трьохзначного числа. В нашому випадку точка K знаходиться в 4-U зоні на схід від осьового меридіану на відстані 612,844 км.

Запропонована система прямокутних координат Гаусса - Крюгера дозволяє звести спотворення за кривизну Землі до незначної похибки.

Орієнтування