ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ

Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

σ u = γ 2u; u(L) = P2

.pdf

Скачиваний:

Добавлен:

24.08.2019

Размер:

8.3 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3621 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

ГЛАВА 3

207

Далее рассматривается одномерная фильтрация. Используя (3.49), (3.50) и (3.57), получаем уравнение фильтрации газа с учетом сорбции (газ

принимается идеальным):

∂ P =	k ∂		∂ P	+	(1− m)sP0 q(t) .
		P
			∂ y
∂ t mµ ∂ y					mρ0

Примем, что изотерма сорбции линейна, т. е. а(Р) = аР. Учиты- вая (3.57) и проводя обычную линеаризацию, вместо последнего уравнения получаем

∂ P2

= χ ∂ 2P2

− b

∂

F(t − τ )[P2

(τ , y) − P2

]dτ ;

(3.58)

∫

∂ t

∂ y2

∂ t

kPcp

2(1

− m)saP

χ =

;

b =

0 ,

mµ

mρ0

где Р1 – начальное давление; Рср – среднее давление.

Проанализируем на основе уравнения (3.58) особенности фильтра- ции газа в сорбируемых средах. Вначале упростим уравнение (3.58). Из- вестно, что коэффициент диффузии молекул газа в твердом теле имеет ве-

личину порядка 10−9 ÷10−8 с. Поэтому характерное время диффузионного процесса может значительно превышать гидродинамическое время. Так, например, для блоков размером 10–2 см это время составляет порядка не- скольких суток, что значительно превышает обычные времена традицион- ных лабораторных исследований на кернах. Для блоков разме-

ром 10−1 ÷100 см времена диффузии соизмеримы с периодом эксплуатации залежи. Исходя из приведенных оценок, в уравнении (3.58) можно пренеб- речь членом в левой части, в результате чего получается

∂ 2P2	= β	∂	t	F(t − τ )[P2 (τ , y) − P2	]dτ , β = bχ −1	,	(3.59)
			∫
∂ y2		∂ t		1
			0

где F(t) – оригинал функции (σ −1D)1/ 2 (1+ σT )−1thl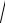σD−1 .

Очевидно, что решения уравнения (3.59) описывают квазистацио- нарные фильтрационные течения, когда медленные изменения характери- стик потока определяются процессами диффузии.

Рассмотрим одномерную фильтрацию газа через образец длиной L

при заданном перепаде давления. Для этого необходимо решить уравне- ние (3.59) при условиях

P2 (0, y) = P2	;	P2 (t, L) = P2	(t);	P2 (t,0) = P2	(t);	P (0) = P .
1		1		2		1	1

Применим для решения задачи (3.58), (3.59) преобразование Лапласа, обозначив u = P2 :

vk.com/club152685050 | vk.com/id446425943

208

ГЛАВА 3

Решая сформулированную задачу для объемного расхода газа, полу-

чаем

Q ≈

k P2 − P2

Dσ

thl

(3.60)

2µP

1+ σT

Переходя к оригиналам, для больших значений t будем иметь

∆P2

D ∂

Q(t) ≈

(t) + 2βL

∫ R(t − τ )∆P2 (τ )dτ ,

(3.61)

2µP L

∂ t

D t

exp −

− exp

−

где ∆P2 = P2 (t) − P2

(t);

R(t)

≈

π 2

−

Если T <<

= T ,

т. е.

диффузия является лимитирующей стадией

процесса, то (3.61) упрощается:

D ∂

t − τ

2βL

Q(t) = 2µP L ∆P

∂ t

−

(τ )dτ .

(3.62)

∫ exp

∆P

Сравним соотношения (3.61) и (3.62) при постоянном значении раз-

ности квадратов давления ∆P2 . В соотношении (3.62) дебит Q(t)

монотон-

2βL2D

но уменьшается

от

Q(0) =

∆P

до Q(∞) =

∆P

2µP L

С учетом кинетики сорбции, т. е. при

Т ≠ 0 ,

при постоянном ∆P2 де-

бит Q(t) меняется от Q(0)

до Q(∞) немонотонно, проходя через максимум

при

−1

D −

DT .

При D = 0 из (3.62) получаем линейную связь между ∆P2

и Q . От-

метим, что эта связь остается линейной, несмотря на зависимость от вре- мени, поскольку полученное решение справедливо при временах, значи- тельно превышающих гидродинамическое время установления режима

течения, равное χ .

Рассмотрим влияние диффузии на зависимость Q = Q(∆P2 ). Не трудно показать, что сорбция газа породой оказывает существенное влия- ние на фильтрационные характеристики. С этой целью проведем следую-

vk.com/club152685050 | vk.com/id446425943

ГЛАВА 3

209

щий иллюстративный расчет. Перепишем (3.62) в безразмерных перемен- ных, приведя его к виду

y(t) = x(t) + a

∂

−

t − τ

(3.63)

∂ t

∫ exp

x(τ )dτ ,

y(t) =

2µL P

Q(t),

x(t) =

∆P2

;

a =

2βL2D

P22

Положим a = 1,

что является реальным значением. Пусть x(t)

изме-

няется ступенчато через интервал времени Т2 = 0,1Т1. Поскольку течение квазистационарное, примем, что период времени T2 также значительно превышает гидродинамическое время установления режима. При этом в течение времени наблюдения на одном режиме расход Q(t) меняется не более чем на 7–8%, что находится в пределах погрешности обычных экс- периментов на керне. Таким образом, формально традиционная методика экспериментальных исследований выполняется. Тем не менее вид зависи-

мости Q − ∆P2 определяется в данном случае последовательностью изме-

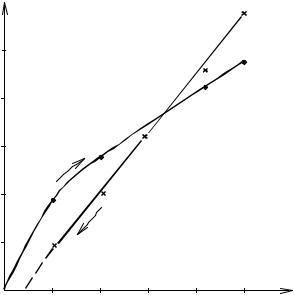
нения перепада давления. На рис. 3.9 представлены расчетные зависимо- сти, полученные при увеличении (кривая 1) и уменьшении (кривая 2) пере- пада давления. В первом случае полученная зависимость характерна для двучленного закона фильтрации.

q	2
	2
5	1
	1
4

5 ∆P2

Рис. 3.9. Расчетные зависимости q от ∆P2 :

1 – при увеличении перепада давления,

2 – при уменьшении перепада давления

vk.com/club152685050 | vk.com/id446425943

210	ГЛАВА 3
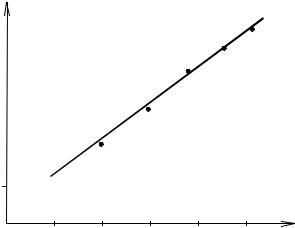
	На рис. 3.10 эта зависимость перестроена в координатах	x	− y , как
	На рис. 3.10 эта зависимость перестроена в координатах	y	− y , как
		y

это обычно делается для проверки справедливости двучленного закона. Вторая зависимость на рис. 3.9 соответствует закону фильтрации с началь- ным градиентом давления. При немонотонном изменении депрессии зави- симость может иметь различный вид (например, S-образная кривая). Кроме того, если по полученным данным определить коэффициент продуктивно- сти (проницаемости) керна, это значение будет кратно отличаться от ис- тинного.

Более сложная ситуация возникает, когда фильтрация газа происхо- дит в неоднородной среде. Пусть, например, в составе пористой среды имеются низкопроницаемые включения, в частности глинистые. Известно, что движение газа через глину начинается при создании определенного критического начального градиента давления. В этом случае газ, сорбиро- ванный породой в низкопроницаемых зонах, при снижении давления вы- деляется не сразу, а после достижения определенного перепада давления между низко- и высокопроницаемой частями и, наоборот, – при повыше- нии давления. При этом фильтрация газа происходит по высокопроницае- мой части. Таким образом, рассматриваются две равномерно перемещен- ные среды с различными параметрами. В соответствии с этим в первом уравнении системы (3.49) поток f представляется в виде двух слагаемых: f = f1 + f2 , где f1 – поток десорбируемого газа из высокопроницаемой среды, f2 – то же из низкопроницаемой.

∆P 2 q

1,0
1,0
0,8
0,8
0,6
0,6
0,4
0,4
0,2
	0			1	2	3	4	5	q
Рис. 3.10. Расчетные зависимости q от ∆P2
Величина потока		f1 подсчитывается по формулам (3.55) и (3.57).
При определении потока			f2	следует учесть наличие критического перепа-

vk.com/club152685050 | vk.com/id446425943

ГЛАВА 3

211

да давления ∆P0 между низко- и высокопроницаемыми частями пористой среды. Это можно сделать, представив поток f2 в виде (см. (3.57)):

а) при снижении давления

F (t − τ )[a

P(τ ) + ∆P ) − C )]dτ

− (1− m)s

∂

∫

∂ t

1,2

f2 = s(1− m)q2 =

(3.64)

при P − P > ∆P ,

при 0

< P1 − P < ∆P0 ,

б) при повышении давления

− (1− m)s

∂

∫

F (t − τ )[a

(P(τ ) − ∆P ) − C )]dτ

∂ t

1,2

(3.65)

f2 = при P

− P > ∆P ,

0 при 0 < P − P1 < ∆P0.

Функция F2

совпадает с определенной выше функцией F с точно-

стью до значений параметров. Повторяя вывод уравнения (3.62), легко по-

лучим выражение для расхода Q(t) в данном случае:

t − τ

Q(t) =

(t)+

∂ 2β1L D1

(τ )dτ +

∆P

∫ exp

−

∆P

2µP L

∂ t

(3.66)

t − τ

2β 2L D2

∫ exp

−

(∆P2

(τ ) − γ )dτ

3l2

где индексы 1 и 2 относятся, соответственно, к высоко- и низкопроницае- мым частям пористой среды.

Последнее слагаемое в правой части (3.66) обращается в ноль при ∆P2 < γ . Как следует из (3.66), при достижении определенного пере-

пада давления на зависимости Q(t) = Q[∆P2 (t)] будет наблюдаться излом, что подтверждается результатами экспериментальных исследований.

Рассматриваемая модель допускает обобщение на случай полидис- персной пористой среды, состоящей к тому же из разнородного материала. В этом случае каждый компонент пористой среды обладает своими физи-

ко-химическими и геометрическими параметрами: − li ,						Di , Ti ,		T1,i . С уче-
том этого соотношение (3.61) примет вид
	k		∂	n	t
Q(t) =		∆P2 (t) +		∑	∫ Hi (t − τ )∆P2 (τ )dτ		,	(3.67)

	2µP0L		∂ t i=1		0

vk.com/club152685050 | vk.com/id446425943

212

ГЛАВА 3

где

−

2Lβ Di

exp

− exp −

4li

Hi (t)

3li

π 2

−

Пусть осуществляется режим с ∆P2 = const. Тогда вместо (3.67) по-

лучается

∆P2

Q(t) =

∑ϕ

(t)

(3.68)

2β P0L

i=1

где ϕ

(t) =

−

−1

−

π 2 D

exp −

ϕi (t)

–

функция,

имеющая

один

максимум

или

один минимум

π 2 D

−1

при t

i −

. Поскольку все t

различны, как сле-

дует из (3.68), расход Q(t)

при большом

будет представляться в виде

суммы случайных колебаний и постоянной величины. При этом в случае достаточно большого времени наблюдения, когда ϕi (t) → 0 , будет иметь место стабилизация расхода.

Проведенные расчеты показывают, что при фильтрации газа в сор- бируемых средах использование обычных методик определения законов фильтрации по исследованиям зависимостей Q = Q(∆p) требует учета су- щественной нестационарности процесса. Необходимо проводить исследо- вания в течение весьма длительного времени. Более того, характерное вре- мя переходного процесса в пористой среде, как это отмечалось выше, мо- жет быть соизмеримо со временем разработки газовой залежи. В этих ус- ловиях само понятие закона фильтрации газа как стационарной зависимо- сти между вектором скорости фильтрации и градиентом давления теряет смысл. Поэтому фильтрационные характеристики необходимо определять одновременно с сорбционными.

3.7. Метод построения оценок решения уравнений фильтрации газированной жидкости

Точные решения нелинейных уравнений стационарной фильтрации газированной жидкости найдены в [44–46]. В [47] при некоторых допуще-

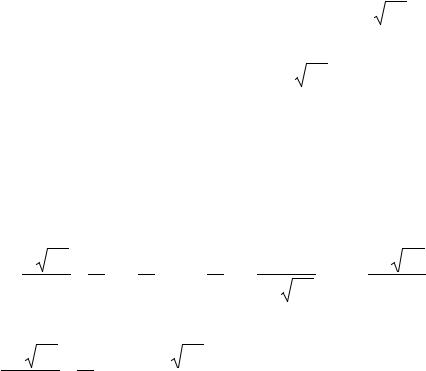
vk.com/club152685050 | vk.com/id446425943

ГЛАВА 3

213

ниях система уравнений газированной жидкости сведена к уравнению теп- лопроводности. Приближенный метод расчета неустановившегося течения газированной жидкости дан в [48], где истинная картина течения заменена расчетной схемой последовательной смены стационарных состояний. Эта же задача решена методом осреднения в [49].

В данном разделе при определенных условиях, наложенных на иско- мые функции, строятся оценки решений уравнений нестационарной фильтрации газированной жидкости в одномерном пласте. Полученные оценки могут быть использованы как приближенные решения с известной погрешностью или для проверки точности различных приближенных ме- тодов.

Отметим, что применению теорем сравнения к оценке решений уравнений нелинейной фильтрации посвящены работы [50–52]. Методы построения оценок решения различных задач теплопроводности даны

в[53, 54].

1.Получим сначала вспомогательные соотношения. Пусть в облас-

ти D{0 < x < l; t > 0} с границей Γ задано уравнение

∂

∂u

k(x, t)

(3.69)

∂x

∂t

∂x

Пусть функция u(x, t)

является решением первой краевой задачи для

уравнения (3.69) в области D. Предположим, что выполняются условия

∂ k ≤ 0 ,

∂ k

≥ 0 ,

∂ u ≥ 0 ,

∂ u ≤ 0 .

(3.70)

∂ x

∂ t

∂ x

∂ t

По теореме сравнения с учетом (3.70) получаем, что функция u(x, t)

ограничена снизу функцией u1 (x, t) ,

которая совпадает с u(x, t)

на грани-

це Γ области D и удовлетворяет уравнению

∂ 2u

∂u

k (x;t) ≤ k .

1 ∂x

∂t

Для построения верхней оценки функции u(x, t) введем

∂ x

y = ∫

k(x, t)

При этом уравнение (3.69) перейдет в

∂ 2u

∂ u

∂ u x 1 ∂ k

= k ∂ t − k

∂ y 0∫

∂ t d x ,

∂ y2

k 2

а область D преобразуется в область D {0 < y < y(t); t > 0 } с границей Γ ,

l	dx
где y(t) = ∫		.
где y(t) = ∫	k(x,t)	.
0	k(x,t)
0

Отсюда, в силу условия

vk.com/club152685050 | vk.com/id446425943

214 ГЛАВА 3

Рассмотрим функцию u2 (x, t), являющуюся решением задачи

	∂2u	2	= k	∂ u	2	,
	∂ y2		1	∂ t
u2	(0,t) = u(0,t), u2 (y, 0) = u(y, 0), u2						(y2 , t) = u(l, t)
в области D2{0 < y < y2; t > 0 }, где k1y2 = l ,						k1 ≥ k	(x, t).

∂∂ ux ≥ 0, получаем u2 (y2 , t)≥ u(y2 , t).

Отсюда с учетом (3.70) по теореме сравнения получаем, что в облас- ти D2{0 < y < y2; t > 0} имеет место соотношение u2 (y, t)≥ u(y, t).

Подчеркнем, что построение верхней и нижней оценок решения уравнения (3.69) не зависело от свойств функции k(x,t), требовалось лишь знание границ изменения коэффициентов и выполнение условий (3.70).

2. Для одномерного случая уравнения нестационарной фильтрации газированной жидкости граничные и начальные условия имеют вид [46]

∂

PF(σ )∂ P

= a

∂

(α Pσ + P),

∂

kн (σ )

∂P = a

∂σ .

(3.71)

∂ x

∂ t

∂ x

∂ t

∂ x

P(0,t) = Pc ,

P(l, t) = Pk > Pc ,

σ (l, t) = σ1 ,

(3.72)

P(x, 0) = Pk ,

σ (x, 0) = σ1.

Здесь

a = m µ k −1

, a

= m

k −1,

m –

пористость,

– абсолютная

проницаемость, µ1, , µ2

– вязкость газа и нефти (принимаются постоянны-

ми), α = с s−1 − 1 c = ρ1P−1 (газ считается идеальным), s – коэффициент

растворимости газа в нефти (принимается постоянным), ρ2 – плотность газа при давлении P , F(σ ) = k1(σ )+ sµ1(cµ 2 )−1 k2 (σ ); k1(σ), k2(σ) – фазовые проницаемости, соответственно, для газа и нефти, σ – насыщенность по- рового пространства нефтью, Pc – давление на галерее скважин, Pk – дав-

ление на контуре питания, σ1 – начальное значение нефтенасыщенности.

Учитывая условия (3.72), сделаем физически очевидные предполо- жения о монотонном поведении искомых функций

∂P	≤ 0 ,	∂P	≥ 0 ,	∂σ	≤ 0 ,	∂σ	≥ 0 .	(3.73)
∂t		∂x		∂t		∂x
Обозначим	σ (0, ∞) = σ 2 . Тогда,				как	следует из (3.72),		(3.73),
при 0 < x < l , t > 0 имеем
			σ 2 ≤ σ ≤ σ1.					(3.74)

Оценим неизвестную величину σ 2 . Для этого найдем стационарное решение системы (3.71).

vk.com/club152685050 | vk.com/id446425943

ГЛАВА 3

215

Введем функции

H1(x) = P∫ k2 (σ )dP ,

H2 (x) = P∫ PF(σ )dP ,

d 2H1 = d 2H2

= 0 .

dx2

Отсюда получаем

k2 (σ )

= const .

PF(σ )

Тогда величину можно определить из соотношения

k2 (σ 2 ) =

Pck2

(σ1)

(3.75)

F(σ 2 )

pk F

(σ1)

Перейдем к построению оценок решений системы (3.71). Исключив

из системы (3.71) величину

∂σ

, получим

∂ t

∂

PF(σ )

∂P − a1αP

∂

(σ )

∂P

= a (1+ ασ ) ∂P .

(3.76)

∂t

∂x

a2 ∂x

∂x

Рассмотрим случай α > 0 .

По теореме сравнения имеем

P′(x, t) ≤ P(x, t)≤ P′′(x, t),

(3.77)

где функции P′(x, t), P′′(x, t) являются, соответственно, решениями урав- нений

∂

a α P

∂ P′

P′F(σ ) −

k k

(σ )

= a

(1+ α σ )

;

(3.78)

∂ x

∂ t

∂

α P

∂ P′′

∂P′′

P′′F(σ ) − 1

k k

(σ )

= a (1+ α σ )

(3.79)

∂ x

∂ t

и удовлетворяют условиям (3.72).

Представим уравнения (3.78), (3.79) в виде

F(σ )

a α P k

(σ )

∂

(P′)

n+ 2

a (1+ α σ )

∂ (P′)

n+ 2'

∂

−

(3.80)

(P′)n

(P′)n+1

∂ x

∂ t

∂ x

(P′)n+1

a α P k

(σ )

∂

(P′)

n+ 2

a (1+ α σ ) ∂ (P′)

n+ 2′

∂ F(σ )

−

(3.81)

(P′)n

(P′)n+1

∂ x

∂ t

∂ x

(P′)n+1

Величина

постоянной

n ≥ 0

в (3.80), (3.81) выбирается из усло-

вия n(α + 1)≥ α (1+ n) Pk

. Далее предположим, что справедливы неравенст-

ва

vk.com/club152685050 | vk.com/id446425943

216 ГЛАВА 3

k (σ )

1+ α

−

Pk k

(σ )

> 0,

(3.82)

(σ )+

α 1

−

(σ )

≤ 0.

dσ

Очевидно, что неравенства (3.82) выполняются при не слишком ма-

лых σ , так как a a−1

~ 10− 2 , α ~ 1. Условия (3.82) вместе с (3.73) позволя-

ют применить к уравнениям (3.80), (3.81) результаты п. 1.

Получаем, что функция P1(x, t),

которая является в D нижней оцен-

кой для P(x, t):

P′(x, t) ≤ P(x, t)≤ P′′(x, t),

удовлетворяет уравнению

∂ 2 (Pn+ 2 )

∂

(Pn+

2 )

∂ x2

∂ t

(3.83)

F(σ ) − a a−1αPhP−hk

(σ )

A = Pn+1P

−n

max

σ 2 <σ

≤σ

(1+ α σ )

и условиям (3.72).

(y, t),

являющаяся верхней оценкой для функции P(y, t)

Функция P2

в области D2{0 < y < l2;

t > 0}

(y, t)≥ P′′(y, t)≥ P(y, t),

удовлетворяет уравнению

−1

∂ 2 (Pn+ 2 )

= A

∂(Pn+ 2 )

y = P

n l

a αPn

∫

F(σ )−

(σ )

dx ,

∂ y2

∂ t

= a P− 2n−1

max

(1+ ασ )F(σ )−

a1αPcn

(σ ) ,

σ 2 ≤σ ≤σ 1

P− n

max

(σ )−

a1αPcn

(σ ) = l

σ 2 ≤σ ≤σ 1

и условиям (3.71).

Решения соответствующих задач имеют вид

n+2

2 ∞ 1

π 2m2 A t

π m x

(3.84)

(x,t) = Pc

(Pk

− Pc

+ π

) l

∑ m exp

−

sin

m=1

P2n+2 (y,t) = Pcn+2 + (Pkn+2 − Pcn+2 )

∑

exp

− π

sin

π m y .

(3.85)

A l2

2 2

Для определения расхода жидкости или газа при

x = 0 необходимо

оценить величину

∂P (0, t) .

∂ x

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3621 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
21.08.2019452.81 Кб3ПРОЕКТНЫХ РЕШЕНИЙ ПРИ РАЗРАБОТКЕ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ.pdf
#
15.09.2019315.6 Кб11Производство, хранение и выдача сжиженного природного газа.pdf
#
10.08.2019638.81 Кб28Происхождение нефти и газа.pdf
#
21.08.2019677.05 Кб6происхождения нефти и газа.pdf
#
16.08.2019226.07 Кб17Процессы и аппараты нефтегазопереработки и нефтехимического синтез.pdf
#
24.08.20198.3 Mб24ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ.pdf
#
10.08.2019220.54 Кб10развитие процессов нефтегазообразования и нефтегазонакопления.pdf
#
19.08.2019608.44 Кб12РАЗЛИВЫ НЕФТИ И НЕФТЕПРОДУКТОВ.pdf
#
17.08.2019955.13 Кб35Разработка нефтяных месторождений ответы.pdf
#
18.08.2019512.21 Кб11Разработка нефтяных месторождений.pdf
#
19.08.20193.99 Mб30РАЗРАБОТКИ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ.pdf