Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ

.pdf

Скачиваний:

Добавлен:

24.08.2019

Размер:

8.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3611 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

Глава 2

107

Введем следующие детерминированные моменты:

∞∆p(r , t)tnd t ,

∆p(r , 0)

∫

mn =

∞∫ Q(t)tnd t ,

n = 0,1, 2,K

0 0

Вычисление моментов производится по экспериментальным дан-

ным ∆p(r0 , t) и Q(t). С другой стороны, можно записать

d n

M n = lim

[(− 1)

∆p(r0 , s)]

(2.33)

∆p(r0 , 0)

s→0 dsn

d n

mn = lim

[(− 1)n Q(s)]

→0 dsn

∞

где ∆p(r0 , s) = ∫ ∆p(r0 , t)exp(− st)d t .

Используя (2.32), (2.33) после ряда элементарных преобразований,

получим следующие равенства:

+ m ln

4χ

∆p(r , 0)

+ m

+ m ln

∆p(r , 0)

16χ

4χ

+ 2m

+ m

4χ

∆p(r , 0)

64χ

16χ

Используя выражения для М0 и М1 и формулу Дюпюи

p ln

= ∆p(r , 0),

(2.34)

можно определить параметры пласта из следующей системы:

2		32	M1		− m1
R0	=	32	M1		− m1
						− m0	,
χ		5	M	0	− m	− m0	,
				0	0

к h		R2				Q						1
	=	0					0								,	(2.35)
µ	=	χ		8π ∆p(r					, 0)	M	0	− m		0	,	(2.35)
							0				0			0
		ln	R0		=	к h		2π ∆p(r0 ,0)					.
		ln	r		=								.
			r		µ				Q
			0						0

Следует отметить, что использование равенства (2.34) не является принципиальным, так как вместо него можно воспользоваться выражением для М2 .

vk.com/club152685050 | vk.com/id446425943

108

Глава 2

В качестве примера обработки рассмотрим кривую восстановления давления, представленную в табл. 2.2.

Моменты, рассчитанные по этим данным, равны:

M		0	= 7,3	103 с ,	m = 6,6 103 с ,
		0			0
M	1		= 4,1	107 с2 ,	m = 3,3 107	с2 .
	1				1

Используя эти значения, из (2.35) получим параметры пласта:

R2	= 3,1 104 с ,	кh		10−14	м3			R
0			= 29			,	ln	0	= 11,1.
χ		µ	= 29			,	ln	r	= 11,1.
χ		µ			Па с			r
								0

Таблица 2.2

Параметры кривой восстановления давления

t, с		0	6 103	12 103	18 103	24 103	30 103
∆p(r0 , 0), МПа		4,84	2,03	0,90	0,38	0,15	≈ 0

3
Q(t),	см	793	307,2	109,3	47,3	15,2	≈ 0
Q(t),	с	793	307,2	109,3	47,3	15,2	≈ 0
	с

Пример 2.

Рассмотрим следующий метод диагностирования реологических свойств вязкоупругопластичных нефтей по данным наблюдения их движе- ния по трубам.

Реологическая модель, описывающая движение вязкоупругопла-

стичных сред, имеет вид
	∂τ					∂υ		∂ 2υ
θ		+τ	− τ	0	= µ		+ λ			,	(2.36)
θ		+τ	− τ		= µ		+ λ			,	(2.36)
	∂ t					∂ r
	∂ t					∂ r		∂ t ∂ r
где τ – напряжение сдвига, υ = υ (r, t) – скорость среды на расстоянии r от
оси трубы; τ 0 – предельное			напряжение				сдвига;		µ		– вязкость среды;
θ , λ – времена релаксации.

Для конкретных сред некоторые из параметров τ 0 , θ , λ могут ока- заться равными нулю.

Пусть нефть в трубе первоначально покоится. В момент времени t=0 перепад давления вдоль оси трубы скачкообразно увеличивается от нуля

до постоянного значения	p0 − p1	, после чего в процессе установления
	L

стационарного режима течения производятся замеры средней по сечению

vk.com/club152685050 | vk.com/id446425943

Глава 2

109

скорости течения w = w(t). Пренебрегая сжимаемостью среды, изменение средней скорости можно описать моделью

− p

− 2τ

0 R

θ d

w + (1 + 2 a λ ) d w + 2 a w =

ρ L

d t2

d t

t =0 = 0,

d w

t =0 = 0 ,

d t

где ra =

8µ

, ρ – плотность среды, R, L – радиус и длина трубы, p

, p –

ρ R2

давления в начале и конце трубы.

Легко получить, что детерминированные моменты

∞(w − w(t))tid t , i = 0, 1

∫

∞

определяются выражениями

= 1+ 2a λ w ,

∞

− p

1 + 2aλ

−

2a ρ l

− p − 2τ

0 R

где w

– предельное значение скорости течения.

∞

2a ρ L

Для диагностирования реологических свойств воспользуемся сле-

дующими соотношениями:

= 1 + 2aλ

−

(2.37)

1 + 2a λ

M 0

= 1 + 2aλ

(2.38)

∞

w∞ ρ L

(2.39)

p0 − p1 − 2τ 0

Анализ этих выражений показывает, что возможно выполнение сле-

дующих условий:

w∞ ρ L

M 0

(θ = 0, λ = 0);

M 0

w∞

− p1 − 2τ

II.

≠

M 0

w∞ ρ L

(θ ≠ 0, λ = 0);

M 0

w∞

− p1 − 2τ

vk.com/club152685050 | vk.com/id446425943

110

Глава 2

III.

≠

w∞ ρ L

(θ = 0, λ ≠ 0);

w∞

− p1 − 2τ

IV.

≠

M 0

≠

w∞ ρ L

(θ ≠ 0, λ ≠ 0).

M 0

w∞

− p1 − 2τ 0

Значения параметров τ 0 и 2 a можно определить по формуле (2.39),

измеряя	p0	− p1	и w для двух установившихся режимов течения с раз-
измеряя			и w для двух установившихся режимов течения с раз-
		L	∞
		L		M1
ными скоростями. Затем можно подсчитать значения отношений				M1	,
ными скоростями. Затем можно подсчитать значения отношений				M 0	,
				M 0

M 0 , которые должны удовлетворять одному из условий I–IV. Определив, w∞

таким образом, какие из параметров θ и λ существенные, их численные значения можно найти по формулам (2.37), (2.38).

2.1.6. Решение обратных задач методом модулирующих функций

Впредыдущем разделе были приведены алгоритмы определения па- раметров моделей, использующие решения краевых задач, полученные в пространстве Лапласа. Применимость этих алгоритмов ограничена сле- дующими причинами.

1.Использование преобразования Лапласа возможно только для линейных моделей.

2.Форма теоретического решения может быть такова, что определить па- раметры оказывается затруднительным.

3.Для аппроксимации весьма сложных реальных граничных и начальных условий используется ограниченное число простых соотношений. В ря- де случаев это может привести к столь большим погрешностям в опре- делении параметров, что использование краевой задачи для идентифи- кации модели становится невозможным.

Всвязи с этим ниже рассматривается метод модулирующих функ- ций, позволяющий определить параметры модели без использования ре- шений краевых задач [14]. По этому методу идентифицируемое дифферен- циальное уравнение заменяется некоторыми интегральными аналогами, из

которых составляются алгебраические уравнения относительно искомых параметров. При этом получаются выражения, в которых отсутствуют производные экспериментальных функций, чем ликвидируются трудности, связанные с непосредственным дифференцированием экспериментальных

vk.com/club152685050 | vk.com/id446425943

Глава 2

111

функций. Следует отметить, что применение метода модулирующих функ- ций требует привлечения большого объема экспериментальной информа- ции. Это является неизбежной платой за возможность нахождения оценок параметров без решения прямой задачи. Для примера рассмотрим задачу определения коэффициента температуропроводности а в уравнении

		ut − auxx = g				(2.40)
по результатам наблюдений
		yi j = u(xi , t j )+ ε i j .
Умножим	(2.40)	на	функции		Ψ(x) = (x − xi )2 (xi′ − x)2		и
Φ(t) = (t − t j )(t j′	− t) такие, что
Ψ(xi ) = Ψ(xi′ ) = 0 ;		Ψ′(xi ) = Ψ′(xi′ ) = 0 ;			Φ(t j )= Φ(t j′ )= 0 ,	(2.41)
и проинтегрируем по x и t в пределах [xi , xi′ ] и [t j ,t j′ ]. Выполнив интегри-
рование по частям, получим алгебраическое уравнение
		Ai i′ j j′ a = Bi i′ j j′ ,				(2.42)
t j′ xi′				t j′ xi′
где Ai i′ j j′ = ∫ ∫ u Φ Ψ′′ d x d t ,			Bi i′ j j′ = − ∫ ∫ (u Φ′ + g Φ) Ψ d x d t .
t j	xi			t j	xi

Как видим, производные экспериментальной функции заменены производными точно известных функций Ψ(x) и Φ(t), дифференцирова- ние которых является корректной операцией. Так как экспериментальные данные представлены в виде дискретных измерений, то вычисление инте- гралов производится численно, по формулам приближенного вычисления интегралов. При этом вместо значений U (x, t) подставляются соответст-

вующие значения замеров y.

Функции Ψ(x) и Φ(t), позволяющие, благодаря свойствам (2.41), из-

бавиться от дифференцирования экспериментальных данных, называются модулирующими функциями. Выбирая различные интервалы [xi , xi′ ]

и [t j ,t j′ ], а также различные функции Ψ(x) и Φ(t) (удовлетворяющие ус- ловиям (2.41)), можно получить систему уравнений вида (2.42), которая решается относительно а методом наименьших квадратов. Для того чтобы определить статистические свойства оценок аˆ , нужно оценить воздейст- вие интегральных операторов на случайные поля y(xi , t j ). Можно пока-

зать, что метод модулирующих функций обладает резкими сглаживающи- ми свойствами [14]. Дисперсия оценки параметра по методу модулирую- щих функций может быть сделана весьма малой, если привлекается доста- точно большой объем экспериментальной информации.

vk.com/club152685050 | vk.com/id446425943

112	Глава 2
Рассматривая более общий случай, отметим, что для того, чтобы
«снять» производную n-степени		∂ n u	, нужно использовать модулирую-
		∂ zn

щую функцию ϕ (z), удовлетворяющую условиям

ϕ(α ) = ϕ ′(α ) = L= ϕ (n−1)(α ) = 0 ,

ϕ(β ) = ϕ ′(β ) = L= ϕ (n−1)(β ) = 0 .

Тогда

β	∂	n	u	β
∫ϕ				d x = (− 1)n ∫ u ϕ (n) d z .
	∂ zn
α				α

2.2. Регуляризация некорректно поставленных задач

Пойди туда, не знаю куда, принеси то, не знаю что.

Одна из первых некорректно поставленных задач.

Как уже говорилось ранее, многие обратные задачи, связанные с ин- терпретацией косвенных наблюдений, оказываются некорректными. Как показывают многочисленные примеры, неустойчивость всегда обусловли- вается тем, что решение задачи ищется в слишком широком классе.

Устойчивость задачи можно восстановить некоторым сужением класса возможных решений за счет привлечения какой-либо дополнитель- ной (априорной) информации количественного или качественного харак- тера. Иными словами, некорректно поставленные задачи возникают тогда, когда мы стремимся смоделировать процесс, не обладая для этого доста- точной информацией. Различные способы решения некорректных (по Адамару) задач отличаются видом используемой дополнительной инфор- мации.

Итак, рассмотрим обратную задачу оценки u по системе наблюде-
ний yi = g(xi ) + ε i для модели
A[u]= g(x), u F , g G ,	(2.43)

где оператор А осуществляет непрерывное взаимно однозначное отобра- жение F → G .

Будем предполагать единственность решения обратной задачи (2.43), т. е. предположим, что если для некоторой функции g(x) уравнение (2.43)

имеет решение u , то только одно.

Задача (2.43) становится корректной, если сузить класс возможных решений u до некоторого компакта М. Это следует из топологической тео- ремы, согласно которой взаимно однозначное и непрерывное отображение

vk.com/club152685050 | vk.com/id446425943

Глава 2	113
компактного пространства М в метрическое пространство N есть гомео-
морфизм [4–6]. Компакт М называется классом корректности	зада-
чи (2.43).

Задача (2.43), в постановке которой указано, что u принадлежит ком- пакту М, называется корректной по Тихонову (условно корректной). Од- ним из способов устойчивого решения уравнения (2.43) является миними-

зация функционала

Au − g

на множестве корректности М (

– норма

элемента g в G). Элемент

uδ

= Argin f

Au − gδ

u M

называется квазирешением уравнения (2.43) [4]. Предполагается, что вме- сто g эксперимент дает gδ такое, что g − gδ ≤ δ ; при δ → 0 , в силу ус- ловной корректности задачи, uδ → u . Квазирешение определено так, что не обязательно gδ N = AM .

На рис. 2.4 изображена ситуация, когда gδ AM . В этом случае ква-

зирешение uδ есть решение уравнения Auδ = ϕδ , где ϕδ		– проекция gδ
на множество N. Часто множество корректности М можно задать с помо-
щью некоторого неотрицательного неоднородного функционала Ω :
M = {u F	Ω(u)≤ m}.

В этом случае естественен также альтернативный методу квазире-
шения подход – минимизация функционала Ω(u)		на множестве

Au − gδ ≤ δ .
	A
M	AM

ϕδ uδ

gδ

Рис. 2.4. Квазирешение некорректно поставленной задачи

Обычно величина функционала Ω (называемого стабилизирующим) характеризует гладкость решения u. Можно показать [5], что этот метод эквивалентен минимизации функционала

M α [u, gδ ]=

Au − gδ

2 + αΩ(u)

(2.44)

на всем пространстве, причем

положительный

параметр α = α (δ ) должен,

по идее метода, определяться по невязке из условия

Auα − g

= δ ,

где uα

– экстремаль функционала (2.44).

vk.com/club152685050 | vk.com/id446425943

114 Глава 2

При таких α имеет место сходимость uδα (δ ) → u , если δ → 0 . Обо-

значим через Rα (gδ ) оператор, ставящий в соответствие элементу gδ эле- мент uδα :

uδα = Rα (gδ ),

Rα (gδ ) называется регулирующим оператором для задачи (2.43) [4–6].

При практическом применении метода параметр α остается, по су- ществу, неопределенным. Обычно проводят расчеты с несколькими значе- ниями параметра α , составляющими геометрическую прогрессию (напри-

мер, 10−1,10− 2 ,10−3,K). Из полученных результатов выбирают наилуч- ший – чтобы решение не было ни слишком сглаженным (слишком боль- шие α ), ни слишком «разболтанным» (слишком малые α ).

В качестве стабилизатора можно взять, например, выражения типа

b	n			d	к	u		2
b	n			d		u
Ωn [u(s)]= ∫d s ∑ pк				(s)			,
									(2.45)
						к			(2.45)
a	к =0			d s
где pк (s) – весовые функции, pк (s)>0.
Отметим, что регуляризующий функционал (2.44) со стабилизатором
b d 2u

Ω2 [u]= ∫		2	d s
a d s

предложен Филлипсом (D. L. Phillips) для случая

A[u(s)]= b∫ K(x, s)u(s)d s ,	c ≤ x ≤ d .
a

2.3. Выбор сложности идентифицируемой модели

Если в задаче меньше трех переменных, это не задача; если больше восьми – она неразрешима.

Из сборника «Физики шутят»

Успех дела зависит от упрощения и от обоснования этого упрощения.

В. Акимов

Априорные сведения о структуре модели изучаемого процесса часто отсутствуют, поэтому вид модели приходится восстанавливать в ходе ре- шения обратной задачи (идентификация в широком смысле этого слова). Как показывает опыт, в условиях неустойчивости большое значение имеет

vk.com/club152685050 | vk.com/id446425943

Глава 2

115

выбор оптимальной сложности математической модели. Излишнее услож- нение модели может привести к неустойчивым алгоритмам идентифика- ции и, как правило, лишает идентификационные модели предсказательной силы.

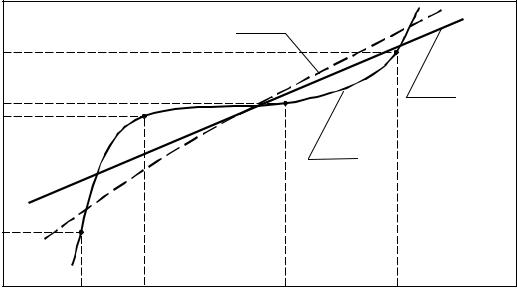
В качестве простого примера рассмотрим задачу восстановления эм- пирической зависимости y = F(x) по экспериментально замеренным точ-

кам {xi, yi}, i = 1, ...,4 (рис. 2.5).

Отклонения экспериментальных точек от графика функции F(x), по- казанного на рис. 2.5 пунктирной линией, объясняются неизбежными ошибками замеров.

Зависимость y = F(x) можно аппроксимировать следующими моде- лями возрастающей сложности:

I)y = a x + b;

II)y = a x2 + b x + c;

III)y = a x3 + b x2 + c x + d,

где коэффициенты a, b, c, d определяются методом наименьших квадратов. Полученные таким образом зависимости для моделей I и III пред- ставлены на рис. 2.5 кривыми 1 и 2 соответственно. Как видно, модель III аппроксимирует зависимость y = F(x) хуже, чем более простая модель I,

особенно при попытке экстраполяции («прогноза») за интервал [x1; x4].

y		F(x)
		F(x)
y4
y3			1
y3
y2
			2
y1
x1	x2	x3	x4	x
Рис. 2.5. Аппроксимация функции полиномами различной сложности

Для слишком сложной модели малые ошибки замеров, незаметные на интервале интерполяции, на этапе прогноза становятся «монстрами», радикально меняющими поведение кривой. По сходному поводу Я. Б. Зель-

vk.com/club152685050 | vk.com/id446425943

116

Глава 2

дович писал: «Положение вещей напоминает сказку Андерсена, в которой тень, отделившись от человека, начинает жить самостоятельно, делает

карьеру и, наконец, заставляет самого человека служить ей» (цитата, при- веденная в [15]).

Таким образом, при выборе разумной сложности математической модели необходим всесторонний анализ, принципы которого не до конца формализуемы. Как отмечается в [15], «умение правильно выбрать мате- матическую модель находится на грани науки и искусства. Оно требует не только необходимых математических и прикладных знаний и опыта, но также вкуса и чувства соразмерности».

Метод структурной минимизации среднего риска

Итак, при постановке и решении задач идентификации моделей по эмпирическим данным ограниченного объема возникает проблема пра- вильного соотнесения сложности идентифицируемой модели с количест- вом и уровнем погрешности имеющихся данных. Эта проблема может быть решена при помощи метода структурной минимизации среднего рис- ка [16, 17]. Оказывается, что если на допустимом множестве решений за- дать структуру, то наряду с минимизацией эмпирического риска (невязки) внутри элементов структуры появляется дополнительная возможность ми- нимизации по элементам структуры. Это позволяет найти решение, даю- щее более глубокий гарантированный минимум среднего риска, чем реше- ние, доставляющее минимум эмпирического риска на всем допустимом множестве решений. По существу, метод структурной минимизации сред- него риска является способом формализации давно применяемого на прак- тике приема регуляризации за счет огрубления модели (см. также [8]).

Рассмотрим сущность этого метода на примере классической задачи восстановления функциональной зависимости y = F(x) по эмпирическим данным, представленным в виде совокупности замеров (выборки) {xi; yi}, где yi – результат измерения y при x = xi, i = 1, 2, ..., l, l – число замеров (объем выборки). Обращаясь к вероятностной интерпретации погрешно-

стей в исходных данных, введем аддитивную помеху ε : yi = F (xi) + εi,

где случайная величина ε имеет нулевое математическое ожидание Е[ε] = 0 и конечную дисперсию D[ε]< ∞. Несмотря на то, что задачи восстановле- ния эмпирической зависимости не относят к некорректно поставленным, при ограниченном объеме выборки возникает проблема правильного соот- несения «сложности» приближающей (пробной) функции с объемом и ка- чеством (уровнем погрешности) исходных данных. Использование излиш- не сложных моделей, содержащих большое число искомых параметров,

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3611 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
21.08.2019452.81 Кб3ПРОЕКТНЫХ РЕШЕНИЙ ПРИ РАЗРАБОТКЕ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ.pdf
#
15.09.2019315.6 Кб11Производство, хранение и выдача сжиженного природного газа.pdf
#
10.08.2019638.81 Кб28Происхождение нефти и газа.pdf
#
21.08.2019677.05 Кб6происхождения нефти и газа.pdf
#
16.08.2019226.07 Кб17Процессы и аппараты нефтегазопереработки и нефтехимического синтез.pdf
#
24.08.20198.3 Mб24ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ.pdf
#
10.08.2019220.54 Кб10развитие процессов нефтегазообразования и нефтегазонакопления.pdf
#
19.08.2019608.44 Кб12РАЗЛИВЫ НЕФТИ И НЕФТЕПРОДУКТОВ.pdf
#
17.08.2019955.13 Кб35Разработка нефтяных месторождений ответы.pdf
#
18.08.2019512.21 Кб11Разработка нефтяных месторождений.pdf
#
19.08.20193.99 Mб30РАЗРАБОТКИ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ.pdf