
ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ
.pdf
vk.com/club152685050 | vk.com/id446425943 |
|
|
ГЛАВА 1 |
|
27 |
τ1 |
τ2 |
|
τ2 |
|
|
τ0 |
|
|
|
|
|
τ1 |
τ2 |
|
τ2 |
|
|
|
|
|
τ1 |
τ2 |
|
τ2 |
|
|
τ0 |
|
|
|
|
|
τ1 |
τ2 |
|
τ2 |
|
|
|
|
|
Рис. 1.6. Фрактальная модель мозга |
|
|
Отметим, что самоподобной в каком-то смысле является и история науки. Американский методолог Джеральд Холтон показал [13], что науч- ная мысль из века в век ходит по одним и тем же кругам, рассматривая (на все более высоком уровне) одни и те же вечные темы: тему первичных частиц, тему происхождения сложных форм из простых, тему самопроиз- вольного появления новшеств и т. д. По этому поводу С. В. Мейен отме- тил: «Будь это шахматная партия, любой арбитр давно бы признал ничью ввиду повторения ходов».
Одной из таких вечных тем является и само понятие фрактальности. Ведь еще Лейбниц в «Монадологии» писал: «Всякую часть материи можно представить наподобие сада, полного растений, и пруда, полного рыб. Но каждая ветвь растения, каждый член животного, каждая капля его соков есть опять такой же сад или такой же пруд» [13].
vk.com/club152685050 | vk.com/id446425943
28 |
ГЛАВА 1 |
1.2. Детерминированный хаос
Совершенно случайный рисунок – увы, также и наиболее скучный...
Непредсказуемость (случайность) желательна с точки зрения разнообразия или неожиданности, но если мы хотим, чтобы рисунок выглядел привлекательно,
необходима некоторая упорядоченность.
Дж. Пирс
Изучение ньютоновской динамики приучило нас к мысли о том, что если заданы силы, действующие между частицами, а также начальные по- ложения и скорости частиц, то уравнения движения позволяют предсказать развитие системы с любой степенью точности для любого сколь угодно позднего момента времени. Это убеждение укрепляется удивительной точ- ностью, с которой механика предсказывает движение планет, моменты солнечных затмений, рассчитывает движение космических ракет. Случай- ность, наблюдаемую в реальном мире, мы обычно связываем с внешними шумами, наличием очень большого числа степеней свободы или же с кван- товыми эффектами.
Настоящим потрясением для научного мира было осознание того, что неупорядоченные, непредсказуемые движения возможны в детермини- рованных динамических системах, т. е. объектах, эволюция которых опи- сывается некоторой системой дифференциальных или разностных уравне- ний, задающих правило однозначного определения будущего, исходя из заданных начальных условий [2–5, 15, 20, 21].
Хаотическое состояние, в котором могут находиться динамические системы без источников случайных шумов, получило название детерми-
нированного (или динамического) хаоса.
Детерминированный хаос отличается от обычного (или шумового) хаоса, понимаемого как состояние полной дезорганизации. Хаос в динами- ческих системах относится к ограниченной случайности, им можно управ- лять и даже прогнозировать на короткие промежутки времени вперед.
Различие между этими двумя видами хаоса подобно различию между шумом в переполненном случайными людьми зале и шумом, создаваемым музыкантами оркестра, готовящимися к началу выступления. Достаточно одного жеста дирижера, чтобы шум в оркестровой яме затих, в то время как овладеть вниманием толпы практически невозможно.
Следует отметить, что необходимым условием возникновения хао- тического движения является наличие особой нелинейности.
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 1 |
29 |
Различается детерминированный хаос в консервативных системах, в которых механическая энергия (или какой-либо ее аналог) сохраняется, и в диссипативных системах (системах с «трением»). Мы в дальнейшем будем рассматривать в основном диссипативные системы.
Выявление и анализ детерминированного хаоса оказывается весьма полезным при управлении сложными движениями в самоорганизующихся системах.
Во-первых, если в некоторой динамической системе диагностируется динамический хаос, то можно надеяться, что некоторым изменением пара- метров (настройкой) можно упорядочить ее движение.
Во-вторых, переход от детерминированного к хаотическому движе- нию происходит по некоторым универсальным сценариям, число которых невелико. Информация об этих сценариях может быть использована для назначения режимов работы, исключающих возникновение хаотических колебаний.
В-третьих, в современной теории нелинейных динамических систем развиты новые методы количественного анализа хаотических колебаний, которые с успехом могут быть использованы для идентификации характе- ра движения и состояния объектов управления.
Возникновение хаотических движений в детерминированных систе- мах возможно, если траектории движения обнаруживают сильную зависи- мость от начальных условий (траектории «разбегаются»). Впервые на это при изучении неинтегрируемых движений трех тел обратил внимание А. Пуанкаре (H. Poincare, 1892 г.), который писал: «...иногда небольшая разница в первоначальном состоянии вызывает большое различие в окон- чательном явлении. Небольшая погрешность в первом вызвала бы огром- ную ошибку в последнем. Предсказание становится невозможным...» По- добные идеи о возможности проявления хаотических движений в детерми- нированных системах высказывались также Биркгофом (G. D. Birkhoff, 1935 г.).
Таким образом, детерминированный хаос проявляется в том случае, когда задача Коши для уравнений движения является некорректно постав- ленной.
Напомним, что математическая задача называется корректно постав- ленной, если:
1)ее решение существует;
2)оно единственно;
3)решение устойчиво относительно малых изменений исходных данных (т. е. малые изменения исходных данных ведут к малому изменению
решения).
Из предыдущего ясно, что возникновение детерминированного хаоса связано с нарушением третьего условия (условия устойчивости).
vk.com/club152685050 | vk.com/id446425943
30 |
ГЛАВА 1 |
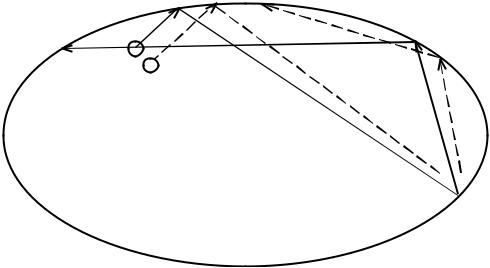
Простейшая механическая система, в которой наблюдается «разбе- гание» траекторий, представляет собой бильярдный шар, ударяющийся и упруго отскакивающий от сторон эллиптического бильярдного стола
(рис. 1.7).
Если начальное положение шара (1) чуть-чуть изменится (положе- ние 2), то уже через несколько соударений шар будет двигаться по совер- шенно другой траектории. Эта неустойчивость приводит к тому, что при сохранении энергии для столов определенной формы шар случайно блуж- дает по столу, никогда не повторяя свою траекторию.
Известным литературным примером, иллюстрирующим сильную за- висимость эволюции системы от начальных условий, является научно- фантастический рассказ Р. Бредбери «...И грянул гром», в котором гибель бабочки, случайно раздавленной в прошлом путешественником во време- ни, так влияет на ход истории, что приводит к существенному изменению настоящего.
|
|
А1 А2 D2 |
|
D1 |
1 |
C1 |
|
C2 |
|||
|
|
||
|
|
2 |
 B2
B2
B1
Рис. 1.7. «Разбегание» траекторий бильярдного шара
Приведем еще один простой пример, иллюстрирующий нарушение устойчивости.
Пусть последовательность задается следующей рекуррентной фор- мулой
xn+1 = 1 − 2 | xn |, n = 0,1, 2, ...
Рассмотрим поведение получаемых по этой формуле последователь- ностей в зависимости от начальной точки x0 из отрезка [0,1].
Возьмем сначала в качестве |
х0 десятичные числа с одним знаком |
|
после запятой. Так, |
например, для |
х0 = 0,1 получим х1 = 0,8 , х2 = −0,6 , |
х3 = 0,2 , х4 = −0,6 , |
х5 = 0,2 и т. д., то есть последовательность вышла на |
|
предельный цикл из двух чисел.

vk.com/club152685050 | vk.com/id446425943
ГЛАВА 1 |
31 |
Аналогичная картина наблюдается для всех других чисел с одним |
|
знаком после запятой, кроме х0 = 0,5 . В этом случае получаем |
х1 = 0 , |
х2 = −1, х3 = −1, ..., т. е. последовательность сходится. |
|
|
Рассмотрим теперь в качестве х0 числа с двумя знаками после запя- |
той. |
Например, х0 = 0,12 . В этом случае последовательность выходит на |
цикл, содержащий 10 чисел. |
|
|
Расчеты показывают, что аналогичная картина будет наблюдаться |
для всех чисел, кроме 16 чисел вида 0,05 × (i + 10( j − 1)), i = 1, 2, 3, 4, 6, 7, |
|
8, 9; |
j = 1, 2 , и трех чисел вида 0,25 × k , k = 1, 2, 3 . |
Для чисел с тремя знаками после запятой имеем четыре варианта по- ведения траектории предельного цикла. К предыдущим 3 вариантам до- бавляется вариант, в предельном цикле которого 50 чисел.
Продолжая увеличивать число знаков после запятой в x0 , можно на-
блюдать дальнейшее усложнение динамики системы.
Этот пример наглядно показывает, что желание считать как можно с большей «точностью» может привести не только к бесполезной потере времени, но и к потере адекватности описания за счет перехода на траек- тории движения, радикально отличающиеся от истинных. Таким образом, при моделировании нелинейных систем необходимо особое внимание об- ращать на определение оптимальной сложности модели (см. по этому по- воду также раздел 2.3 данной книги).
1.2.1. Странный аттрактор
Эволюцию динамических систем удобно представить в геометриче- ской форме, используя фазовое пространство. Рассмотрим, например, дви- жение маятника с трением, описываемое системой уравнений
m ddtυ = −mg xl − αυ,
dx = υ,
dt
где x – отклонение маятника от точки равновесия, m – масса маятника, α – коэффициент трения, υ – скорость движения маятника, l – длина маятника, g – ускорение свободного падения.
На фазовой плоскости (x,υ ) движение маятника представляется в
виде спирали, наматывающейся на точку О (0, 0) (рис. 1.8, а). Эта точка как бы «притягивает» к себе все траектории движения, из каких бы точек они не исходили. Поэтому точка равновесия О (0, 0) называется аттрактором этой динамической системы (от слова attract – притягивать).

vk.com/club152685050 | vk.com/id446425943
32 |
ГЛАВА 1 |
υ
υ
M0
x
x
предельный
цикл
а) |
б) |
Рис. 1.8. Аттракторы динамических систем
Поскольку часто нас интересует только установившееся движение, то при рассмотрении диссипативных систем можно ограничиться нахож- дением их аттракторов – областей фазового пространства, притягивающих траектории. Это значительно облегчает исследование динамических сис- тем.
Кроме точек равновесия динамические системы могут иметь аттрак- торы в виде предельных циклов – замкнутых кривых в фазовом пространст- ве (см. рис. 1.8, б). Так как при движении по замкнутой кривой изобра- жающая точка все время возвращается в некоторое фиксированное состоя- ние, то предельный цикл соответствует периодическим колебаниям.
При изменении параметров динамической системы может меняться число аттракторов и их устойчивость. Подобные явления называются би- фуркациями, а те значения параметров, при которых изменяются качест- венные свойства движения, называются критическими или бифуркацион-
ными.
Приведем любопытный пример с натуральными числами, в котором проявляются аналоги понятий аттрактора и бифуркации. Возьмем любое натуральное двузначное число a (напр., а = 27 ). Поменяв между собой
цифры этого числа, получим число а , которое назовем инверсным к a
(в нашем случае а = 72). Далее поступим следующим образом. Вычислим разность этих чисел (из большего вычитаем меньшее, для нашего примера
b = а − а = 72 − 27 = 45 ) и рассмотрим сумму полученного числа и ин-
версного к нему b + b (для нашего примера 45+54=99). Можно убедиться, что при вышеприведенной последовательности действий с любыми двузначным числом в ответе получится 99 или 0 (в случае одинаковых цифр в числе, например 44), т. е. с какого бы двузначного числа мы не начинали, в конце приходим к 0 или 99! Таким образом, эти два числа являются как бы «притягивающими числами» и исполняют роль
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 1 |
33 |
бы «притягивающими числами» и исполняют роль своеобразных аттракто- ров.
Посмотрим теперь, что будет происходить, если те же действия про- вести с трехзначными числами. Непосредственным перебором убеждаем- ся, что для трехзначных чисел количество «аттракторов» также будет рав- но двум (0 для «симметричных» чисел типа 333, 121, … и 1089 для всех прочих чисел). А вот для четырехзначных чисел число «аттракторов» бу- дет уже равно пяти (0,990, 9999, 10890, 10989), т. е. происходит своеобраз- ная «бифуракция». Продолжая эксперименты с увеличением числа цифр (перебор осуществляется с помощью несложной компьютерной програм- мы), определим соответствующее количество «аттракторов». Для нату- ральных чисел с количеством цифр от 1-го до 11-ти результаты расчетов приведены в таблице:
Количество цифр в числе |
Количество «аттракторов» |
|
1 |
|
1 |
2, |
3 |
2 |
4, |
5 |
5 |
6, |
7 |
13 |
8, |
9 |
34 |
10, |
11 |
89 |
Из таблицы видна закономерность проявления «бифуркаций»: уве- личение числа «аттракторов» происходит с увеличением числа цифр на два.
Числа в правой колонке таблицы удивительным образом связаны с числами Фибоначчи: 1, 1, 2, 3, 5, 13, 21, 34, 55, 89, 144, …, т. е. число «ат-
тракторов» увеличивается по закону чисел Фибоначчи с нечетными номе- рами. Обнаруженная закономерность может быть строго доказана.
Данный пример мы приводим также для того, чтобы показать, как через «простое» можно проиллюстрировать такие достаточно сложные по- нятия, как аттрактор и бифуркация. Неслучайно одним из проявлений ин- теллекта считают умение видеть различие в сходном и сходство в различ- ном.
Рассмотрим теперь явление бифуркаций на примере динамической системы.
dxdt = λx + y − x(x2 + y2 ), dydt = − x + λy − y(x2 + y2 ).
Перейдя к полярным координатам, x = r cosϕ , y = r sinϕ , получим r& cosϕ − rϕ& sinϕ = r sinϕ + λ r cosϕ − r3 cosϕ ,

vk.com/club152685050 | vk.com/id446425943
34 |
ГЛАВА 1 |
|
|
& |
& |
3 |
sinϕ , |
r sinϕ + rϕ cosϕ = λ r sinϕ − r cosϕ − r |
|
||
где r =  x2 + y2 .
x2 + y2 .
Сложив первое уравнение, умноженное на cosϕ , со вторым уравне- нием, умноженным на sinϕ , и отняв от второго уравнения, умноженного
на cosϕ , первое уравнение, умноженное на sinϕ , получим |
|
|||
dr |
= r(λ − r2 ), |
|
||
|
|
(1.4) |
||
dt |
|
|
||
|
dϕ |
= −1. |
|
|
dt |
|
|
||
Из (1.4) следует, что исходная система имеет решения, соответст- вующие постоянным значениям r = rc . Они могут быть найдены из усло-
вия |
dr = 0, откуда r |
= r |
= 0 и r |
= r = λ (при λ > 0 ). |
|
|
dt |
c |
0 |
c |
1 |
|
|
|
|
|
|
Первое решение соответствует точке покоя О (0, 0), а второе – пре- дельному циклу, представляющему собой движение по окружности с ра- диусом против часовой стрелки с постоянной угловой скоростью ω = 1.
Исследуем устойчивость этих решений.
Предположим, что система в момент времени была выведена из по- ложения равновесия О (0, 0) и отклонилась от нее на малое расстояние ε . Полагая r = r0 + ε = ε , получим из (1.4) с точностью до линейных по ε
членов
|
dε |
= λ ε , |
|
|
|
|
|
|
dt |
|
|
откуда с учетом начального условия имеем |
|
||
|
ε = ε 0eλ t . |
(1.5) |
|
Согласно (1.5) при λ < 0 значение ε |
экспоненциально убывает со |
||
временем, т. е. точка О (0, 0) является устойчивой точкой равновесия (ат- трактором).
При |
λ > 0 |
начальное малое отклонение растет |
по закону eλ t , |
||
т. е. точка равновесия теряет устойчивость. |
|
|
|||
Для |
исследования |
устойчивости |
предельного |
цикла положим |
|
r = r1 + ε1, что дает |
dε1 = −2λ ε1 , |
|
|||
|
|
|
|
||
|
|
|
dt |
|
|
откуда ε1 = ε 0e− 2λ t , т. е. ε1 → 0 при λ > 0 |
(устойчивый предельный цикл), |
||||
а при λ < 0 |
отклонение от предельного цикла со временем возрастает. |
||||
Величина λ |
в (1.5), |
характеризующая экспоненциальную скорость |
|||
расхождения (или схождения) двух исходно близких траекторий с ε 0 = 0

vk.com/club152685050 | vk.com/id446425943
ГЛАВА 1 |
35 |
и ε 0 > 0 , называется показателем Ляпунова. Потеря устойчивости движе-
ния происходит в тот момент, когда показатель Ляпунова становится по- ложительным. Из этого примера ясно, что показатель Ляпунова определяет чувствительность траектории к изменению начальных условий. Поэтому эта величина может быть использована в качестве количественной харак- теристики, «измеряющей» детерминированный хаос.
Таким образом, при постепенном увеличении от отрицательных зна- чений к положительным в точке λ = 0 происходит бифуркация: устойчи- вая точка равновесия переходит в устойчивый предельный цикл. Эта би- фуркация называется бифуркацией Хопфа (E. Hopf, 1942 г.). Соответст- вующая бифуркационная диаграмма приведена на рис. 1.9.
Точка покоя и предельный цикл являются примерами инвариантных множеств – встроенных в фазовое пространство объектов, отображаю- щихся сами на себя в ходе эволюции системы.
Совокупность инвариантных множеств, имеющихся в фазовом про- странстве данной динамической системы, во многом определяет характер движения, поэтому эта совокупность называется фазовым портретом
системы.
x&

 x
x
0 |
λ |
Рис. 1.9. Бифуркация Хопфа
Решающую роль в определении структуры фазового портрета играет теорема единственности решений системы обыкновенных дифференци- альных уравнений, связанная с именами О. Коши (A. Cauchy, 1820–30 гг.) и Э. Пикара (E. Picard, 1891–96 гг.). Эта теорема утверждает, что при до- вольно «мягких» условиях на функции fi (x) существует единственное
решение задачи
|
dxi |
|
= f |
i |
(x , x |
2 |
,..., x |
n |
), |
(1.6) |
||||
|
|
|
|
|||||||||||
|
|
|
dt |
|
|
1 |
|
|
|
|||||
x |
|
|
= x |
|
, |
i =1,2,...,n, |
|
|||||||
|
|
|
|
|||||||||||
i |
|
t =0 |
|
i0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
если только начальное состояние не представляет собой точку покоя.
При рассмотрении фазового пространства это означает, что пересе- чение двух траекторий в точках, отличных от точки покоя, невозможно.
vk.com/club152685050 | vk.com/id446425943
36 |
ГЛАВА 1 |
Если же говорить о предсказуемости движения, то именно единственность решения задачи Коши долгое время поддерживала уверенность в невоз- можности случайных движений динамических систем. Однако, как уже отмечалось, движение может стать непредсказуемым, если траектории не- устойчивы относительно малого изменения начальных значений.
«Разбегание» траекторий само по себе еще не приводит к стохастич- ному поведению. Необходимо еще существование некоторых статистиче- ских закономерностей, наличие средних по времени величин, связанных с тем, что система вновь и вновь возвращается в состояния, близкие к ис- ходным. Такие движения возможны, если в фазовом пространстве имеются незамкнутые траектории, бесконечно и беспорядочно блуждающие внутри некоторой ограниченной области. Подобные траектории образуют инвари- антные множества, которые в случае диссипативных систем являются ат- тракторами.
Более подробные исследования показывают, что аттракторы, на ко- торых реализуются хаотические движения, имеют фрактальную структуру, т. е. характеризуются дробной размерностью. Причину этого легко понять, если процесс перепутывания траекторий представить себе как перемеши- вание «фазовой жидкости».
Возьмем множество траекторий, которые в начальный момент вре- мени исходят из близких точек, образующих маленький фазовый объем – каплю «фазовой» жидкости. Предположим, что эта «капля» отличается по цвету от остальной жидкости внутри рассматриваемой области фазового пространства (рис. 1. 10).
Если в этой области есть устойчивая точка покоя, то «капля» стянет- ся в эту точку (см. рис. 1.10, а). При наличии аттрактора в виде предельно- го цикла капля через некоторое время растянется вдоль него и «окрасит» лишь узкий поясок в его окрестности (см. рис. 1.10, б). На аттракторе хао- тической системы (см. рис. 1.10, в) капля жидкости испытывает повторное влияние растяжения и изгиба, что, как мы уже убедились на примере пре- образования подковы (п. 1.1.3), приводит к образованию фрактальной структуры. При этом «капля» хорошо перемешивается с неокрашенной жидкостью и образует характерные разводы, более или менее равномерно окрашивая всю притягивающую область.
За связь с непредсказуемым хаотическим движением, а также за на- личие фрактальной структуры аттракторы динамических систем, демонст- рирующих хаотическое движение, получили название странных аттрак- торов (strange attractor). Понятие о странных аттракторах было введено Рюэлем и Таккенсом (D. Ruelle, F. Takens, 1971 г.) при обсуждении пере- хода к турбулентности.
