
ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ
.pdf
vk.com/club152685050 | vk.com/id446425943
188 |
ГЛАВА 3 |
где s – массовое содержание в единице объема пор частиц примеси, осев- ших на поверхности пор скелета пористой среды, q – скорость увеличения содержания загрязняющих частиц за счет закачки свежих порций жидкости с примесями, α – коэффициент, определяющий скорость выноса загряз- няющих частиц потоком жидкости (предполагается, что скорость выноса пропорциональна содержанию осевших частиц).
Аппроксимируя в первом приближении зависимость проницаемости
пористой среды от степени ее загрязненности линейной функцией, примем k = k0 − ε s ,
где k0 – проницаемость незагрязненной пористой среды.
Выразив s через k, получим
λ dkdt + k = k∞ ,
где λ – характерное время загрязнения, λ = α1 , k∞ – предельное значение
проницаемости, k∞ = k0 − ε αq .
Как правило, k∞ << k0 , поэтому можно положить k∞ = 0 , что после интегрирования дает
− t
k = k0e λ .
Согласно этой модели уменьшение проницаемости вследствие загря- нения пористой среды должно описываться простой экспоненциальной за- висимостью. Однако эксперименты показывают, что это справедливо толь- ко для пористых сред, представленных хорошо отсортированным кварце- вым песком узких фракций. Экспериментальные данные, полученные в на- сыпных пористых средах из песка широких фракций, уже не подчиняются экспоненциальной зависимости. Промысловые исследования также приво- дят к кривым падения приемистости нагнетательных скважин, отличным от экспоненты.
Отмеченные факты можно объяснить многомасштабностью размеров поровых каналов. Пусть ρ (r)dr – объемное содержание поровых каналов масштаба r , k0 (r) и λ (r) – проницаемость и характерное время загрязне-
ния для этих каналов. Тогда суммарная проницаемость пористой среды выражается интегралом
|
∞ |
ρ (r)e− |
t |
|
|
|
dr , |
||
k = |
λ (r ) |
|||
|
∫ |
1 |
|
|
где ρ1(r) = k0 (r)ρ (r). |
0 |
|
|
|
|
|
|
|
|
vk.com/club152685050 | vk.com/id446425943
190 |
ГЛАВА 3 |
|
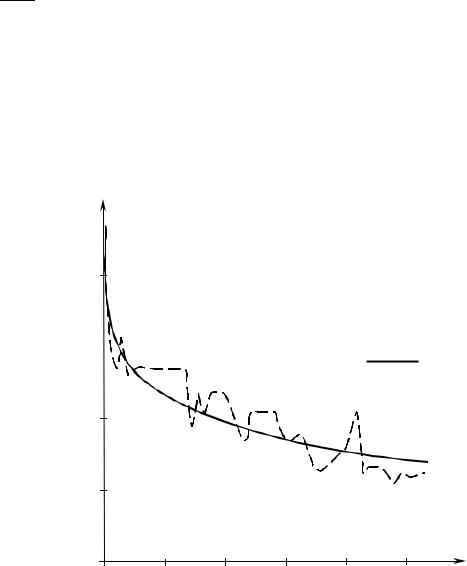
Расчеты показали, что экспериментальная зависимость хорошо опи- |
||
сывается выведенной нами формулой, если принять α = 0,57 , |
β = 0,32 , |
|
t = Vпор . |
Обратная задача определения коэффициентов α и β |
решалась |
методами теории чувствительности (см. раздел 2.1.1).
Динамика набухания глин
В настоящее время в нефтяной промышленности находят широкое применение технологии, основанные на взаимодействии химических реа- гентов с монтмориллонитовыми глинами. В частности, полимерглинистые суспензии используются для изоляции промытых зон пласта и увеличения нефтеотдачи. Кроме того, применение химреагентов позволяет за счет их взаимодействия с глинистым цементом значительно изменять проницае- мость и пористость глиносодержащих коллекторов.
Для количественной оценки влияния минерализации воды и закачки реагентов на набухание глин проводятся лабораторные исследования (на- пример, с помощью прибора Жигача–Ярова) зависимости коэффициента набухания от времени.
При обработке данных этих исследований необходим выбор модели, адекватным образом описывающей динамику набухания. Учитывая фрак- тальную иерархичность строения глин, для обработки кривых набухания можно предложить многоэкспоненциальную зависимость вида
N |
|
− |
t |
|
|
|
|
|
, |
||
|
λ |
||||
k = k∞ − ∑ Ai exp |
|
||||
i=1 |
|
|
i |
|
|
где k – коэффициент набухания; k∞ – асимптотическое (при t → ∞ ) зна- чение k ; λi – характерное время набухания структурных единиц i -го уровня, Ai – «вклад» этого уровня в общий процесс набухания.
Для определения величин Ai и λi воспользуемся X-методом А. То- больского [8], первоначально предназначавшимся для оценки времени ре- лаксации напряжения сдвига полимеров.
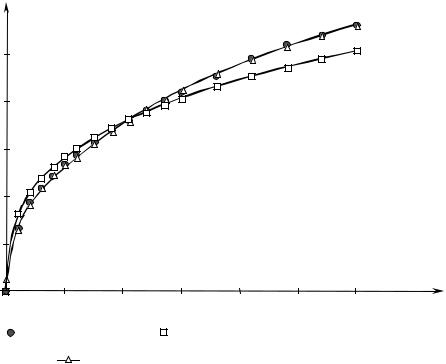
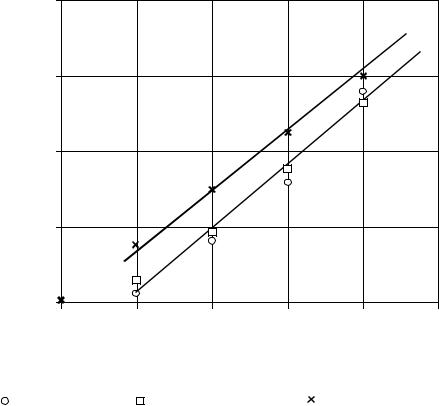
Суть этого метода заключается в том, что кривая k(t) перестраивает- ся в координатах (t, ln(k∞ − k)). При этом в перестроенной кривой выделя- ется прямолинейный участок (соответствующий большим временам), ко- торый описывается зависимостью
ln(k |
∞ |
− k) = ln A |
− |
t |
, |
|
|||||
|
N |
λN |
|
||
|
|
|
|
|
|
по которой оцениваются значения AN и λN (нумерация уровней ведется в порядке возрастания времени релаксации; через N мы обозначили номер высшего наблюдаемого в данной шкале времени уровня организации).
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 3 |
193 |
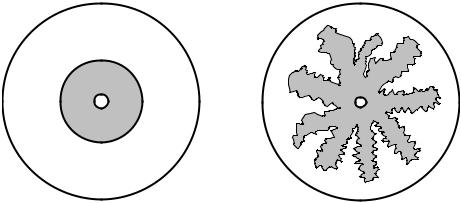
родных зон: «загрязненной» призабойной зоны и расположенной за ней зоны с большей проницаемостью. В ряде случаев эта несколько схематич- ная модель может быть уточнена за счет принятия некоторых дополни- тельных предположений о структуре пласта с ухудшенной проницаемо- стью. В условиях, когда какие-либо теоретические или экспериментальные исследования структуры «загрязненного» пласта отсутствуют, полезную информацию могут дать некоторые положения теории организации слож- ных систем. Так, можно ожидать, что зоны пласта с ухудшенной прони- цаемостью обладают, как и многие другие системы с неупорядоченной структурой, фрактальными свойствами (см. главу 1). Для примера на рис. 3.5 схематически изображен загрязненный пласт в рамках зонально неоднородной (а) и фрактальной (б) моделей.
а) |
б) |
Рис. 3.5. Модели неоднородного пласта
Подчеркнем, что речь здесь идет о пористых средах с крупномас- штабной фрактальной структурой. Этот термин введен нами для того, что- бы подчеркнуть отличие последних от мелкомасштабных фрактальных структур теории протекания [22, 31, 32] и подразумевает выполнение нера-
венства
ξ >> l ,
где l – характерный масштаб изменения градиента давления, ξ – длина корреляции. (Реальная система с фрактальными свойствами на масштабах, больших ξ , является однородной. Грубо говоря, ее можно представить себе как состоящую из фрактальных блоков размерами ξ .)
Причины, которые приводят к образованию крупномасштабных фрактальных структур в изначально однородной пористой среде, весьма разнообразны. Практически все механизмы необратимого роста, рассмат- риваемые в литературе [22, 32], могут проявить себя в процессах нефтега- зодобычи. Так, известно, что фракталы могут образовываться вязкими

vk.com/club152685050 | vk.com/id446425943
194 |
ГЛАВА 3 |
пальцами, возникающими при вытеснении из пористой среды одной жид- кости другой. Поэтому можно ожидать, что крупномасштабные фракталь- ные структуры возникают при закачке в пласт воды, газа и других агентов, поддерживающих пластовое давление, а также при вскрытии пласта за счет проникновения фильтратов буровых и цементных растворов. Достаточно общими механизмами образования фрактальных структур являются агре- гация, ограниченная диффузией, и осаждение. Отсюда следует, что фрак- тальные структуры в пористой среде могут образоваться при ее загрязне- нии – в ходе заиливания призабойной зоны, отложения твердых углеводо- родов, выпадения конденсата и т. д.
3.4.1. Уравнение нестационарной фильтрации на фракталах
Выведем, следуя [33], уравнение нестационарной радиальной фильтрации в средах с крупномасштабной фрактальной структурой. Пусть M (r,t)dr – масса флюида в кольцевом элементе пласта единичной мощно- сти, образованном цилиндрическими поверхностями радиусов r и r + dr :
M (r,t)dr = N(r)M0 (r,t)dr , |
(3.31) |
|
где N(r)dr – число узлов фрактала в кольцевом элементе |
|
|
N(r) = CDrD−1, |
(3.32) |
|
D – размерность фрактала, M0 (r,t) – масса флюида в одном узле фрактала. |
||
Закон сохранения массы флюида можно записать в виде |
|
|
∂ M (r,t) |
= − ∂ G(r,t), |
(3.33) |
∂ t |
∂ r |
|
где G(r,t) – массовый расход флюида через цилиндрическую поверхность радиуса r.
Связь между расходом флюида и градиентом давления принимается
в виде |
K(r) |
N(r)∂ p |
|
|
|
G(r,t) = −ρ |
, |
(3.34) |
|||
|
µ |
|
∂ r |
|
|
где ρ и µ – плотность и вязкость жидкости, |
p – давление. |
|
|||
Величину K(r) естественно назвать проводимостью фрактала, отне- сенной к одному его узлу. Выражение (3.34) следует рассматривать как со- отношение, определяющее величину K(r) аналогично тому, как закон Дарси в форме
υ = − k ∂ p
µ ∂ r
определяет проницаемость пористой среды k .
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 3 |
195 |
Проводимость фрактальных структур подчиняется степенному зако-
ну
K(r) = K1 |
, |
(3.35) |
rθ |
|
|
где θ – показатель, описывающий аномальность проводимости, имеющую место из-за весьма специфического способа комбинирования проводящих узлов во фрактальную решетку.
С учетом сжимаемости флюида
∂ M0 |
= ρV |
β |
∂ p |
, |
(3.36) |
∂ t |
0 |
|
0 ∂ t |
|
|
где β0 – сжимаемость жидкости, V0 – объем узла фрактала.
Из уравнений (3.31)–(3.36) в линейном приближении получим урав- нение пьезопроводности на фрактале
|
χ |
|
∂ |
|
|
|
|
∂ p = |
|
r β ∂ p |
, |
(3.37) |
|||
|
|
|
|||||
∂ t |
rα |
|
|
|
∂ r |
|
|
|
∂ r |
|
|
||||
где χ = |
K1 |
|
, α = D − 1, β = D |
−1−θ . |
|
|
|
|
|||
µV β |
0 |
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
||
Уравнение (3.37) аналогично уравнению пьезопроводности в евкли- |
|||||||||||
довом пространстве размерности d : |
|
|
|
|
|||||||
|
|
|
∂ p = |
|
χ ∂ |
|
∂ p |
|
|
||
|
|
|
|
rd −1 |
. |
(3.38) |
|||||
|
|
|
|
|
|
|
∂ r |
||||
|
|
|
∂ t |
|
rd −1 ∂ r |
|
|
||||
Однако величины α и β в (3.37) могут быть дробными и отличают- ся (θ ≠ 0) друг от друга.
3.4.2. Обработка кривых восстановления давления в пластах с фрактальной структурой
Как уже отмечалось, крупномасштабные фрактальные структуры мо- гут образоваться при вытеснении из пористой среды нефти водой. Поэтому уравнение (3.37) может быть использовано для интерпретации данных гидродинамического исследования скважин, нагнетающих воду в нефте- носные пласты, а также добывающих скважин, в продукции которых со- держится большое количество воды (в этих случаях подвижностью нефти можно пренебречь и рассматривать однофазную фильтрацию во фракталь- ной среде).
Наличие фрактальных структур может быть связано также с загряз- нением прискважинных зон пласта (см. выше). Очистка этих зон, сводя- щаяся к разрушению фрактальных структур, требует значительных затрат времени и средств. Поэтому для уменьшения вероятности проведения очи-
vk.com/club152685050 | vk.com/id446425943
196 |
ГЛАВА 3 |
сток «вхолостую» необходимо разработать способы диагностирования на- личия крупномасштабных фракталов в окрестностях скважины и методы определения их характеристик. Покажем, что эта задача может быть реше- на путем использования данных гидродинамического исследования пла- стов.
|
Прежде всего, рассмотрим исследования на установившихся режи- |
||||||||||||||
мах фильтрации. Из (3.37) при |
∂ p |
=0 легко получить Q = K |
0 |
(p |
k |
− p |
c |
), |
|||||||
|
|||||||||||||||
|
|
|
|
|
|
|
∂ t |
0 |
|
|
|
||||
где K0 |
= |
|
|
λ(1− β ) |
≈ λ(1− β ) – коэффициент продуктивности скважины, |
||||||||||
r1− β − r1− β |
|||||||||||||||
|
|
|
r1− β |
|
|
|
|
|
|
|
|||||
|
|
|
|
k |
c |
k |
|
|
|
|
|
|
|
||
λ = |
K1CD |
, |
Q0 – дебит жидкости в стационарном режиме, rc , rk |
– радиусы |
|||||||||||
µ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
скважины и некоторого контура, на котором поддерживается постоянное давление pk , pc – давление на забое скважины. Поскольку и при отсутст- вии фракталов связь между Q0 и pk − pc линейна, то исследование на ус- тановившихся режимах фильтрации не позволяют выявить наличие фрак- талов.
Эта задача может быть решена путем обработки кривых восстанов-
ления давления (КВД) в остановленных скважинах. Рассмотрим, например, операционный метод обработки КВД (см. [34] и раздел 2.1.4). Пусть в ходе
исследований замеряются дебит жидкости Q(t) и давление на забое сква- |
|||
жины pc (t): |
|
|
|
λr β ∂ p(rc ,t) |
= Q(t), |
(3.39) |
|
c |
∂ r |
|
|
p(rc ,t) = pc (t)
при условиях |
|
|
p(r, 0) = p0 |
(r), p(rk ,t) = pk = const . |
(3.40) |
Здесь p0 (r) – распределение давления, соответствующее стационар-
ному режиму фильтрации до остановки скважины. Осуществив преобразо- вание Лапласа
u(r, s) = |
∞ p (r,t)e− st dt , |
|
||||||
|
|
|
∫ |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
получим |
(r β u′ ) ′ |
|
|
|
|
|||
1 |
− |
s |
u = 0 , |
(3.41) |
||||
|
|
|
||||||
|
rα |
|
r |
r |
|
χ |
|
|
|
|
|
|
|
|
|
||
− λr β u′ |
(r , s) = F(s), |
(3.42) |
||||||
|
|
c r |
|
c |
|
|
|
|
где
p1 = p(r,t)− p0 (r),
