Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ

.pdf

Скачиваний:

Добавлен:

24.08.2019

Размер:

8.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

Глава 2

ментальных функций, что избавит от необходимости дифференцирования последних.

Так, проинтегрировав уравнение (2.13) по времени, получим
	θ =	u(tl ) − u(t1 )					.		(2.17)
	θ =						.		(2.17)
		t
		∫l (1 − u)dt
		t1
Подставив вместо значений u(ti )						замеры yi			и произведя численное
интегрирование, получим оценку
		yl	− y1
θ =								.	(2.18)
θ =	l −1			y	i	+ y	i+1	.	(2.18)
	∆t ∑ 1 −				i		i+1
	∆t ∑ 1 −					2
	i=1					2

В выражении (2.17) отсутствуют производные экспериментальной функции, поэтому (2.18) дает достаточно точный результат. Так, использо-

вание данных математического эксперимента (2.16) при ∆t =0,02 и l = 10

приводит к оценке θ , отличающейся от истинного значения θ = 1 не более чем на 0,3%.

2.1.4. Применение преобразования Лапласа при решении обратных задач

Если алгоритм определения параметров линейной модели связан с получением точного решения прямой задачи, то целесообразно осущест- вить преобразование Лапласа по следующим трем причинам.

1.Как правило, аналитическое решение модели проще получить в про- странстве изображений, чем во временной области.

2.Преобразование Лапласа является интегральным преобразованием,

что приводит к сглаживанию погрешностей экспериментальных функций.

3.Часто, исходя из точного решения в изображениях, удается получить асимптотики при t → ∞ и t → 0 решений во временной области и эф- фективно использовать их при решении обратных задач.

Всвязи с этим методы решения обратных задач, основанные на при- менении преобразования Лапласа, находят весьма широкое применение.

Эксперименты, предназначенные для определения параметров моде- лей, проводятся во временной области, поэтому для того, чтобы можно было осуществить оценивание, необходимо либо решение прямой задачи преобразовать ко времени t, либо экспериментальные данные о процессе перевести в пространство изображений по Лапласу. Ниже рассматривают- ся оба этих способа.

vk.com/club152685050 | vk.com/id446425943

Глава 2

Оценивание во временной области

Если решение прямой задачи может быть переведено во временную область, то используют обычные приемы минимизации суммы квадратов отклонений (раздел 2.1.1). Для облегчения процедуры обращения рассмат- риваются асимптотики s → 0 (t → ∞) или s → ∞ (t → 0) .

Рассмотрим пример эффективного применения преобразования Лап- ласа при решении обратной задачи определения коэффициента диффузии раствора поверхностного активного вещества (ПАВ) в ходе следующего эксперимента.

Вертикальная стеклянная трубка нижним концом погружена в рас- твор ПАВ с постоянной концентрацией c0 . В начальной момент времени в трубке находится столб чистой воды высотой h0 , удерживаемый силами поверхностного натяжения. Раствор ПАВ начинает диффундировать в во- де, за счет чего происходит понижение уровня воды в капилляре, причем это изменение уровня замеряется.

Исходя из формулы c x=h = (h0 − h) ρ2gkr , где k = − ddcσ , σ – коэффи- циент поверхностного натяжения, h – высота столба жидкости, можно вы- числить концентрацию в верхней части столба (величина k определяется в предварительных опытах).

Таким образом, для определения коэффициента диффузии необхо- димо решить обратную задачу оценки величины D из переопределенной системы уравнений

∂ c

+ h′

∂ c = D

∂ 2c

, 0 < x < h(t),

(2.19)

∂ t

∂ x2

∂ x

t =0 = 0,

(2.20)

x=0 = c0 ,

∂ c

= 0

(2.21)

∂ x

x=h(t)

x=h(t) = f (t) ,

(2.22)

где h(t) и f(t) – экспериментально определяемые функции (табл. 2.1). Перейдя к безразмерным переменным

		t			x			h
	=		,	x =		,	h =
t
								h0
		t0			h

vk.com/club152685050 | vk.com/id446425943

Глава 2

и пренебрегая членами порядка h′ ∂∂ cx , получим из (2.19)–(2.22)

∂ c	= D	∂ 2 c	,
∂τ		∂ x 2
	1

τ =0

= 0,

x =0 = c0

∂c

= 0 ,

∂x

x =1

= f

(τ ) = f (t

(2.23)

Dt0

, t0 = 1,8 105

где D1

с, τ = ∫

h 2 (t)

Таблица 2.1 Значения экспериментально определяемых функций h(t) и f(t)

t, c	h 102 , см	c 103 , %
0	1,4200	0,04

75600	1,3598	0,0502

79200	1,3536	0,0564

82800	1,3464	0,0636

86400	1,3368	0,0732

90000	1,3290	0,0810

93100	1,3176	0,0924

97200	1,3086	0,1014

100800	1,2992	0,1108

104400	1,2901	0,1199

108000	1,2812	0,1288

111600	1,2736	0,1364

115200	1,2633	0,1467

162000	1,1680	0,2420

165000	1,1648	0,2452

169200	1,1560	0,2540

172800	1,1516	0,2584

176400	1,1458	0,2642

180000	1,1422	0,2678

vk.com/club152685050 | vk.com/id446425943

100 Глава 2

Далее, применяя преобразование Лапласа по переменной τ , получим

= D

s с

1 dx 2

∞

d c

− sτ

= 0 , где с(x, s)

= ∫ e

c(x,τ )dτ .

x =0

x =1

Решение этой задачи имеет вид

(1 − x)

c =

Используя соотношение (2.23), получим

= F

(s) ,

(2.24)

где

F*(s) = ∞∫ e− sτ f *(τ )dτ .

Известно, что коэффициент диффузии растворов ПАВ имеет поря-

док 10−10 −10−8 м2 , поэтому мы можем воспользоваться для начального

временного интервала следующей асимптотикой:

					s
					s

			exp		D
	s				D
ch	s	≈		1		.
ch	D	≈		2		.
	D			2
	1

С учетом этого из (2.24) следует равенство

		s
	−	s

exp
				F*(s)
		D1	=	F*(s)	.
	s		=	2c0	.
	s			2c0

Переходя в этом равенстве к оригиналам, получим

		1		f (t )
Ф*			=

	2			2c0
		D1τ

или

1	= 2 D1		*−1	f	(t )
		Ф				,
		Ф
τ
τ				2c0

vk.com/club152685050 | vk.com/id446425943

Глава 2

101

где

Ф*(x) = 2

∞

−ξ

dξ ,

∫ e

а через Ф*−1 обозначена функция, обратная к Ф*.

Обозначая Y1 =

Ф*−1

f (t )

, получим

2c0

, Y2

Y2 = α Y1,

α = 2

т. е. в координатах (Y1,Y2 ) экспериментальные данные должны спрямлять-

ся, и угловой коэффициент этой прямой определяет коэффициент диффу-

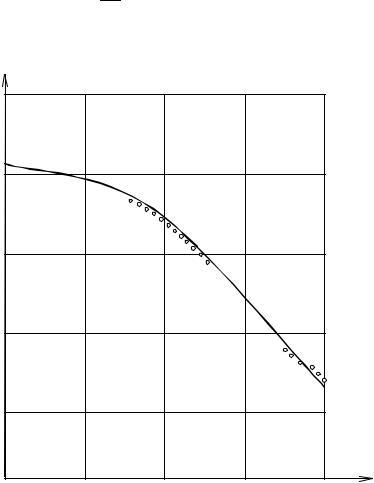
зии D. Результаты обработки экспериментальных данных в координа- тах (Y1,Y2 ) приведены на рис. 2.2, из которого видно, что в данном слу-

чае α = 1, т. е. D = 0,26 10−9 м2 .

0,5

0,4

0,3

0,2

0,1

0,2

0,3

0,4

0,5

Рис. 2.2. Изменение высоты столба жидкости h(t) в капилляре

На рис. 2.3 приведено сопоставление экспериментальных точек с графиком функции h(t), полученной по формулам решения прямой задачи с определенным выше коэффициентом диффузии D.

vk.com/club152685050 \| vk.com/id446425943
102		Глава 2
Оценивание в пространстве изображений
Если решение прямой задачи получено в пространстве изображений
и обращение его затруднительно, то удобнее провести оценивание пара-
метров θ в s-плоскости.		Пусть y(t) – результаты замеров величины u,
u(t, θ ) – решение прямой задачи, G(s) и V(s, θ ) – их изображения. Оцени-
вание параметров в пространстве изображений требует минимизации от-
клонения функции V(s, θ )		от G(s). Интеграл G(s) = ∞∫ e− st y(t)dt можно вы-
					0
числить любым из способов численного интегрирования. В частности, мо-
жет быть использована формула			(yi +1 − yi )(e− sti		− e− sti +1 ),
G(s) =	1 y0	+ 1 ∑	(yi +1 − yi )(e− sti		− e− sti +1 ),
где yi = y(ti ), t0 = 0 .	s	s2 i = 0		ti +1 − ti
где yi = y(ti ), t0 = 0 .
h, м
1,4
1,3
1,2
1,1
1,0
0	0,25		0,50	0,75	1,00	t
Рис. 2.3. Результаты обработки экспериментальных данных
		в координатах (Y1, Y2 )

Отметим, что метод оценивания параметров, который дает равные веса ошибкам в s-области, не гарантирует равные веса ошибок во времен- ной области. Так, если y(t) = u(t,θ )+ ε (t), то минимизация выражения

vk.com/club152685050 | vk.com/id446425943

			Глава 2			103
	s
	∫2		G(s) − V (s,θ )	ds
	∫2		G(s) − V (s,θ )	ds
	s1
			∞
в s-области эквивалентна минимизации ∫W (t)					ε (t)		dt во временной области,
в s-области эквивалентна минимизации ∫W (t)					ε (t)		dt во временной области,
		0
где весовая функция W (t) =	exp(− s1t) − exp(− s2t)					. В результате ранние мо-
где весовая функция W (t) =						. В результате ранние мо-
			t

менты времени «весят» больше, чем поздние. Вводя увеличенные веса при меньших величинах s, можно уменьшить вес, придаваемый ошибкам при малых временных.

Чтобы провести оценивание, необходимо использовать дискретные действительные значения переменной s = si (i = 1,2,3,..., N ). Для каждого si

должны быть вычислены величины G(si ) и V (si ,θ ), и, наконец, выраже-

ние ∑N [G(si ) − V (si ,θ )]2 должно быть минимизировано по параметрам θ .

i=1

Вряде случаев вычисления могут быть значительно упрощены за счет ра- сcмотрения асимптотик решения V (s,θ ) при s → 0 или s → ∞ .

Пример.

Для решения задач оперативного контроля за работой магистраль- ных трубопроводов большое значение имеет вопрос определения коэффи- циента гидравлического сопротивления по результатам технологических измерений, проводимых в процессе эксплуатации трубопроводов. При этом измеряются давления на входе и выходе трубопровода и расход про- дукта.

Неустановившееся движение сжимаемой жидкости в трубопроводах

описывается известной системой линеаризованных уравнений
−	∂ p	=	∂(ρ w) + 2аρ w,
	∂ x		∂ t		(2.25)
	∂ p	= c2		∂(ρ w)
−					,
	∂ t			∂ x

где р – давление, w – среднеобъемная скорость, ρ – плотность жидкости, 2а – коэффициент сопротивления, с – скорость звука.

Задаются следующие начальные и граничные условия:

	ρ w	t =0 = 0 ;		p		t =0 = 0 ,

ρ w	x=0	= ϕ0 (t)	;	p	x=0 = f0 (t).

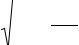
vk.com/club152685050 | vk.com/id446425943

104		Глава 2
	Требуется определить коэффициент а по дополнительному гранич-
ному условию, заданному, например, в виде
	p	x=l = Ψ0 (t),	(2.26)

где l – длина трубопровода.

Исключая ρ w , для определения давления p(x,t) получим уравнение

∂

2 p

∂ 2 p

2al ∂ p

∂ x 2

∂ t

с дополнительными условиями

t =0 = 0 ;

∂ p

= 0 ;

∂ t

t=0

= f (x);

∂ p

w c d

2al

= −

0 0

ϕ ,

x =0

∂ t

d t

x =0

где x =

p =

ϕ =

ϕ0

– характерные

= t ,

ρ0w0

значения соответствующих величин.

Применив преобразования Лапласа, получим, опуская черточку над

безразмерными переменными,

2al

dx2

s U ,

x=0 = F(s),

w c

2al

= −

0 0

Φ ,

x=0

где U, F, Ф – изображения функций p, f, ϕ .

Отсюда

(x, s) = F chγ x − Φ1 shγ x ,

(2.27)

2al

w c s

где γ = s

2 + 2al s , Φ =

Φ .

p0γ

Если Ψ

– изображение функции Ψ0 , то из (2.26) и (2.27) получим

Ψ1 = F chγ − Φ1 shγ .

Для упрощения рассмотрим асимптотику s → 0 . Ограничиваясь ли-

нейными по s членами, получим

w c

2al

Φ(s)

(2.28)

F(s) − Ψ1(s)

где Φ(s) =

Φ(s)

2.1.5. Метод детерминированных моментов

Одним из эффективных методов решения обратных задач является метод детерминированных моментов [8]. Детерминированным моментом n-го порядка называется выражение

дом наименьших квадратов позволяет оценить величины

и 2а.

vk.com/club152685050 | vk.com/id446425943

Глава 2		105
Как следует из (2.28), зависимость между	~	s изображается
Как следует из (2.28), зависимость между	Φ(s) и	s изображается

прямой, не проходящей через начало координат. Придав s несколько дей-

ствительных значений, получим из (2.28) систему, решение которой мето-

ρ0w0c

	M n = ∞∫ tn (u∞ − u (t))d t ,	n = 0, 1,…,
	0
где u∞ – предельное значение характеристики процесса u (t).
Эти моменты могут быть определены как по экспериментальной за-
висимости y(t)	(обозначим их через Мnэ ), так и по теоретической зависи-
мости u (t,θ ),	получаемой из решения	прямой задачи (обозначим

их MnT (θ )). Приравняв соответствующие теоретические и эксперимен- тальные значения моментов, получим соотношения для определения пара-

метров модели θ :

M nT (θ ) = M nэ , n = 0, 1,…, N–1,

где число соотношений N определяется количеством неизвестных пара- метров модели. Кроме того, из величины моментов можно составлять ди- агностические критерии адекватности выбираемой модели реальному про- цессу.

Предполагается, что кривая y(t) задана на достаточно большом ин-

тервале [0, T] так, что y (T ) ≈ u∞ и	∞∫ (u∞ − y(t))tnd t ≈ 0 , поэтому экспери-
	T

ментальные значения моментов вычисляются по приближенной формуле

M nэ ≈ T∫ [u∞ − y(t)]tnd t .	(2.29)
0

При проведении расчетов на практике интеграл (2.29) берется чис-

ленно. Вычисление теоретических значений моментов MnT (θ ) существенно

упрощается, если прямая задача решена операционным методом. Легко
показать [8],	~
показать [8],	что если u (s,θ ) – изображение функции u(t,θ ), то
	T	n		d n u∞	~
	M n (θ ) = (−1)		lim		− u	(s, θ ) .
	M n (θ ) = (−1)		lim		− u	(s, θ ) .
			s→0 dsn s

vk.com/club152685050 | vk.com/id446425943

106

Глава 2

Пример 1.

Определение параметров пласта по данным нестационарных иссле- дований.

Рассмотрим неустановившуюся фильтрацию однофазной жидкости после остановки скважины. Как известно, этот процесс описывается урав- нениями

∂ p

1 ∂

∂ p

= χ

< r0 ≤ r ≤ R0 < ∞ ,

∂ t

∂ r

r ∂ r

p(r,0) = p

= p

−

= p

− p ln

(2.30)

стац

2π к h

p(R ,t) = p

2π r h

∂

p(r ,t)

= Q(t).

∂ r

Здесь приняты следующие обозначения: r0 , R0 – радиусы скважины и контура питания; p0 – давление на контуре питания; Q0 , Q(t) – стацио-

нарный и текущий расходы на забое скважины.

Дополнительное условие для решения обратной задачи по определе- нию параметров пласта задано в виде кривой восстановления давления

p0 − p(r0 , t) = ∆p(r0 , t).

Задача (2.30) в изображениях по Лапласу имеет следующий вид:

стац

−

= −

(2.31)

r d r

d r

d ~

Q(s)

p(R0 , s) =

p(r0 , s) =

d r

∞

где

p(r, s) = ∫ p(r,t)exp(− st)dt ,

∞

Q(s) =

∫ Q(t)exp(− st)dt .

Решение задачи (2.31) представляется следующим выражением:

p* Q(s)

(r, s) =

−

(2.32)

K0 R0

− K0 r

pстац

K0 R0

+ I0 R0

K1 r

где K0 (x), K1(x),

I0 (x), I1(x) – функции Бесселя от мнимого аргумента.

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
21.08.2019452.81 Кб3ПРОЕКТНЫХ РЕШЕНИЙ ПРИ РАЗРАБОТКЕ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ.pdf
#
15.09.2019315.6 Кб11Производство, хранение и выдача сжиженного природного газа.pdf
#
10.08.2019638.81 Кб28Происхождение нефти и газа.pdf
#
21.08.2019677.05 Кб6происхождения нефти и газа.pdf
#
16.08.2019226.07 Кб17Процессы и аппараты нефтегазопереработки и нефтехимического синтез.pdf
#
24.08.20198.3 Mб24ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ.pdf
#
10.08.2019220.54 Кб10развитие процессов нефтегазообразования и нефтегазонакопления.pdf
#
19.08.2019608.44 Кб12РАЗЛИВЫ НЕФТИ И НЕФТЕПРОДУКТОВ.pdf
#
17.08.2019955.13 Кб35Разработка нефтяных месторождений ответы.pdf
#
18.08.2019512.21 Кб11Разработка нефтяных месторождений.pdf
#
19.08.20193.99 Mб30РАЗРАБОТКИ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ.pdf