ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ

Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

равной 1 и в среднеквадратичном смысле, т. е.

.pdf

Скачиваний:

Добавлен:

24.08.2019

Размер:

8.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 369 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

Глава 2

Так, определение и сравнение параметров уравнения пьезопроводно- сти по кривым восстановления давления, снятым до и после обработки скважины, позволяет оценить результативность этой обработки.

Рассмотрим более подробно постановку некоторых типов обратных

задач.

Обратная коэффициентная задача

Пусть изучаемый в эксперименте процесс моделируется решением

задачи
L [u] = g(x,θ ),	x X Rk ,	(2.1)
θ
с дополнительными условиями
lθ [u] = h(x,θ ),	x ∂X .	(2.2)
Здесь x = {x1, x2 , x3,...., xk } – набор так называемых контролируемых
переменных, θ Ω – совокупность некоторых параметров,		Lθ [ ] – детер-
минированный дифференциальный оператор, зависящий		от θ , Rk –

евклидово пространство размерности k, ∂X – граница множества Х.

При заданных θ задача (2.1)–(2.2) интерпретируется как обычная начально-краевая задача математической физики и является прямой зада- чей определения «следствия» (решения) u по «причинам» – набору извест- ных θ , g, h и заданных Lθ и lθ .

Если же величины θ неизвестны, то возникает следующая обратная задача: оценить исходные параметры θ и функцию отклика u = u(x,θ ) для модели (2.1)–(2.2) по экспериментальным данным, если в эксперименте наблюдаются некоторые функционалы b[u] от отклика u [1, 2].

Экспериментальные данные, предоставляющие информацию для оп-


ределенных оценок θ	и u	= u(x,θ ) , могут быть заданы в виде системы на-
блюдений		yir = u(xi ,θ ) + εir ,
		yir = u(xi ,θ ) + εir ,	(2.3)
		i = 1,2,...,n,	(2.3)
		r = 1,2,...,ri ,
где yir – результат r -го измерения u в точке xi , ε ir			– ошибка этого изме-

рения.

Оценки параметров θ , полученные с помощью случайных вели- чин yir , сами являются случайными величинами. Смещенность или несмещенность, а также дисперсия оценок определяется статистическими методами на основе некоторых предположений о распределении случай- ных величин ε ir и о виде функции отклика u(x,θ ) .

vk.com/club152685050 | vk.com/id446425943

Глава 2

Мы будем считать, что параметры θ принадлежат евклидовому про-

странству размерности m:

θ = {θ1,θ 2 ,...,θ m} Ω Rm .

Более общий случай принадлежности искомых характеристик функ- циональному пространству сводится к рассматриваемому подходящей па- раметризацией:

θ (x) = ∑θi fi (x) ,

i=1

где fi (x) – заданные базисные функции.

Дополнительные условия (2.2), а также правая часть (2.1) могут быть известны с ошибками и лишь в отдельных точках.

Пример. Обратная коэффициентная задача теплопроводности

Пусть u = u(x,t) является решением краевой задачи теплопроводно-

сти:

L[u] ≡ ut − a(x,t) uxx = g(x,t), 0 < x < l; 0 < t < T;

u x=0 = u0 (t); u x=l = u1(t), t ≥ 0,

u	t =0	= u0	(x), x X = {0 < x < l}.

Функции g, u0 , u0 , u1 заданы, требуется определить коэффициент теплопроводности a(x,t) .

Представив a(x,t) в виде

a(x,t) = ∑θi fi (x,t) ,

i=1

сведем задачу к получению оценок {θi } по результатам измерений

yij = u(xi ,t j ,θ ) + εij .

Интерпретация косвенных измерений

Пусть объект исследования характеризуется элементами u F ; если элемент u не доступен для прямого изучения, то изучается какое-либо его косвенное проявление g(x), x X .

Элемент g(x) функционально зависит от u:
A[u] = g(x) ,	(2.4)

где A[ ] – некоторый детерминированный оператор.

vk.com/club152685050 | vk.com/id446425943

Глава 2

Обратная задача, связанная с интерпретацией косвенных изменений, заключается в оценке элемента u по некоторым функционалам b[g(x)] от правой части (2.4) при заданном А.

Например, могут производиться измерения в точках x1, x2 ,..., xn X :

yi = g(xi ) + ε (xi ) .

Требуется найти оценку u для модели (2.4).

Оператор А в (2.4), как правило, является вполне непрерывным, так

что он не может иметь непрерывного обратного оператора A−1 [3]. Это приводит к неустойчивости решения обратной задачи (2.4) относительно экспериментальных погрешностей: даже малые ошибки в измерении g мо- гут привести к недопустимо большим ошибкам в определении u. Поэтому

говорят, что обратная задача (2.4) некорректно поставлена [4–6].

После работ Ж. Адамара (J. Hadamar, 1923 г.) считалось, что некор- ректно поставленные задачи нецелесообразно изучать, поскольку ошибки замеров неизбежны, однако насущные потребности практики все чаще приводили к необходимости их рассмотрения.

В конце концов интуитивные методы повышения устойчивости об- ратных задач, выработанные поколениями инженеров и математиков- прикладников, оформились в хорошо разработанную теорию построения

устойчивых (регуляризующих) алгоритмов решения некорректных за- дач [4–6], элементы которой будут рассмотрены чуть ниже.

Пример. Задача определения формы электрического импульса на входе кабеля u(t) по результатам записи его на выходе кабеля формулиру- ется в виде

t
∫ K(t − τ )u(τ )dτ = g(t) ,	(2.5)
0
где K(t) – импульсная функция кабеля.
В ходе эксперимента проводятся наблюдения
y(t) = g(t) + ε (t) ,	(2.6)

где g(t) – сигнал на входе кабеля, ε (t) – ненаблюдаемая ошибка измере- ния g в момент времени t.

Обратная задача определения u(t) по наблюдениям (2.6) параметри-

зацией u(t) = ∑θα fα (t) , где {fα (t)} – некоторая базисная система функ-

α =1

ций, может быть сведена к решению методом наименьших квадратов сис- темы линейных алгебраических уравнений

m
∑Kβα θ α = y(tβ ) ,		(2.7)

α =1

tβ

где Kβα = ∫ K(tβ − τ ) fα (τ )dτ .

vk.com/club152685050 | vk.com/id446425943

Глава 2

Следствием некорректности задачи (2.5) является плохая обуслов-

ленность системы (2.7), что на практике приводит к «разбалтыванию» ре-

шений θ при больших m. Первоначальный подход в этом случае состоял в том, чтобы варьировать величину m в зависимости от величины ошибки ε . Затем появились более тонкие методы решения такого рода задач.

2.1. Методы решения обратных коэффициентных задач

2.1.1. Регрессионный анализ

Если удается решить прямую краевую задачу (2.1–2.2) и получить явный вид функции u = u(x,θ ) , где неизвестные θ присутствуют в виде

параметров, то получение оценок θ сводится к обычной задаче регресси- онного анализа [1, 7–9]. Решение прямой задачи, как правило, нелинейно зависит от θ , так что мы приходим к задаче поиска оценок в случае нели- нейной регрессии. Примем обычные для регрессионного анализа предпо-

ложения о ненаблюдаемых ошибках:

E[εir ] = 0, E[εir εi′r′ ] = δ ii′δ rr′σ i2 ,

1,	i = i′;
где E[ ] – знак усреднения, δ i i′ =	i ≠ i′.
0,	i ≠ i′.

В качестве оценок неизвестных параметров θ используем оценки метода наименьших квадратов:

− u(x ,θ )]2

θ N = Arg inf Φ(θ ),

Φ(θ ) = ∑

[ y

θ Ω

i=1σ i2

(2.8)

= ∑ y

/ r ;

p =

;

N =

∑r ,

где Arginf Φ(θ ) – значение θ , при котором Φ(θ ) достигает минимума.

Множитель

в дальнейшем можно опустить, заменив u и y на

σ 2

y .

Метод стохастической аппроксимации

Потребовав минимизации функционала Φ(θ ) в среднем, вместо (2.8) получим оценки

Arg inf ( ) , где ( ) E[ ( )].

θ = Φ θ Φ θ = Φ θ

θ Ω

vk.com/club152685050 | vk.com/id446425943

Глава 2

Непосредственное определение оценок θ затруднено из-за отсутст- вия информации о функции распределения случайных величин yir , поэто-

му для оценки величин θ может быть использована итерационная гради- ентная процедура

где θ Φ = ∂ Φ

∂θ1

		(s+1)	(s)
		θ	= θ − ρ (s) Φ(θ (s) ) ,	(2.9)
			θ
,...,	∂ Φ
	∂ Φ	.
		.
	∂θ m

Здесь ρ (s) – число, определяющее величину шага и выбираемое

обычно таким, чтобы удовлетворялось условие монотонности

Φ(θ (s+1) ) ≤ Φ(θ (s) ) .

Можно показать [10], что если применяется алгоритм (2.9) и

	∞		∞
а)	∑ρ (s) = ∞,		∑ρ 2 (s)	< ∞ ;
	s=1		s=1
б)	inf {(θ − θ )T Φ(θ ) }≤ 0					(ε > 0) ,
			θ
	ε < (θ − θ )T (θ − θ ) < 1 ;
				ε
в) E[ T Φ Φ] ≤ d(1 + θ Tθ ) (d > 0) ,
	θ	θ
					(s)
							s → ∞ с вероятностью,
то последовательность				θ		сходится к θ при	s → ∞ с вероятностью,

	(s)	(s)
lim	E[(θ	− θ )T (θ	− θ )] = 0.
s→∞

Здесь θ T – транспорированный вектор θ .

Решение обратных задач методами теории чувствительности

При решении обратных коэффициентных задач путем итерационной минимизации невязки большое значение имеет вопрос выбора величины и направления каждого последующего «шага» в пространстве искомых па- раметров.

vk.com/club152685050 | vk.com/id446425943

Глава 2

Оптимизация «маршрута» поиска может быть осуществлена с помо- щью исследования чувствительности решений прямых задач относительно варьирования значений коэффициентов моделей [11, 12].

Используя аппарат теории чувствительности, коэффициенты θ мож- но искать при помощи итерационной процедуры

где смещения ∆θ (s)

θ (s+1) = θ (s) + ∆θ (s) ,

(2.10)

определяются из условия минимизации функционала

ψ (∆θ ) = ∑n

[u(x

,θ (s))+ ∆θ

T h(x ,θ (s))− y

]2 ,

i=1σ i2

T .

h(x ,θ (s))=

∂ u

, ...,

∂ u

∂θ1 ∂θ 2

∂θ m

Матрица чувствительности

h(x ,θ (s))

определяет «отклик» решения

прямой задачи на малые изменения значений коэффициентов θ .

Пример.

Рассмотрим линейное дифференциальное уравнение

				m		d	k	u
				∑θ k		d		u	+ u = θ 0
				k =1		d t k
с начальными условиями
u(k )(0) = α k ,									k = 0,1, ..., m − 1.
Необходимо оценить параметры θ j ( j = 0,1, ..., m) по замерам
	yi = u(ti ) + ε i ,								i = 1, 2, ..., n .
Легко увидеть, что функции чувствительности
				h j (t,θ ) =					∂ u(t,θ )
									∂θ j
могут быть найдены из решения задачи
m	d	k	h0
∑θ	d		h0	+ h = 1,
∑θ	d tk			+ h = 1,
k =1 k	d tk				0
m	d k h j				d ju
∑θ k				+		+ h j = 0, j = 1,2,K,m,
∑θ k	d tk			+	d t j	+ h j = 0, j = 1,2,K,m,
k =1	d tk				d t j
hl (0) = 0,				l = 0,1,K,m.
Оценки коэффициентов θ определяются по алгоритму (2.10), где ве-
личины ∆θ (s) находятся путем решения уравнений
m
∑A(jls)∆θl(s) = B(js) ,									j = 0, 1, …, m,
l =0

vk.com/club152685050 | vk.com/id446425943

Глава 2

где

A(jls) = ∑h h j (ti ,θ (s) )hl (ti ,θ (s) ), i=1

B(js) = ∑h [yi − u (ti ,θ (s) )] hl (ti ,θ (s) ). i=1

2.1.2. Оценивание параметров с помощью замены дифференциального уравнения конечно-разностным

Мы предполагали до сих пор, что прямая начально-краевая зада- ча (2.1)–(2.2) может быть решена точно. Однако это возможно далеко не всегда. В тех случаях когда точное решение задачи (2.1)–(2.2) не удается

получить, для определения параметров может быть произведена замена

операторов Lθ

и lθ их конечно-разностными аналогами.

Рассмотрим, например, задачу оценки коэффициента температуро-

проводности а для уравнения теплопроводности:

∂ u(x,t)

= a

∂ 2u(x, t)

∂ t

∂ x2

(0 ≤ x ≤ l,

t ≥ 0).

Переходя к дискретной координате с шагом ∆x

и к дискретному

времени с шагом ∆t , получим уравнение [13]

uk,s − uk,s −1 = θ (uk +1,s − 2uk,s + uk −1,s ),

(2.11)

∆t

≤ ξ , ξ – методическая ошибка замены дифференци-

где θ = a

a − a

(∆x)2

ального уравнения конечно-разностным.

Требуется оценить θ по системе наблюдений yk,s = uk,s + ε k,s , где

uk,s = u(xk ,ts ),

xk = k ∆x

= 0,1,...,

ts = s ∆t

(s = 0,1,...) ,

∆x

E[ε k,s ] = 0, т. е. E[ yk,s ] = uk,s ,

E[ε

k,s

k ′,s′

] = δ

δ σ 2 .

kk ′ ss′

Для решения задачи перепишем (2.11) в виде

uk,s = uk,s −1 + θ (uk +1,s − 2uk,s + uk −1,s ) .

(2.12)

Заменим теперь в правой части (2.12) все u на результаты их наблю-

дений. Получим в итоге некоторую оценку для uk,s :

− 2 yk,s + yk −1,s ) .

u k,s = yk,s−1 + θ ( yk +1,s

vk.com/club152685050 | vk.com/id446425943

94		Глава 2
В качестве	оценки параметра θ			можно	принять величину
θ = Arginf F (θ ),
θ = Arginf F (θ ),	F (θ ) = E ∑	(uk,s − yk,s )2		, и использовать для ее оп-

	k,s
ределения метод стохастической аппроксимации (2.1.1).
Рассмотрим случай, когда разности			yk − yk ±1		измеряются в малом

числе точек xk . В этих условиях необходимая точность оценок обеспечи- вается достаточно большим числом измерений по времени (s → ∞) .

Исходя из (2.9), получим следующий алгоритм определения оце-

нок θ (s) в момент s∆t :

	(s)		(s−1)	− ρ (s){ θ F (s) (θ ) }θ =θ (s−1) ,
	θ = θ			− ρ (s){ θ F (s) (θ ) }θ =θ (s−1) ,
где	F (s) (θ ) =	1		− y		)2	+ f (s) , f (s) – добавка, обеспечи-
где	F (s) (θ ) =		∑(uk,s	− y		)2	+ f (s) , f (s) – добавка, обеспечи-
θ	θ	2	k		k,s

вающая несмещенность оценок θ (s) .

Так, если конечные разности измеряются в одной точке, можно по-

ложить [13]
		1				2
	F (s) (θ ) =	1					+ 2σ 2 (1+ 3θ ).
	F (s) (θ ) =	2		uk,s − y			+ 2σ 2 (1+ 3θ ).
θ		2	θ		k,s

Легко проверить, что
E[{ θ F (s) (θ )}θ =θ (s−1) ] = 0					при		θ (s−1) = θ n ,

так что добавка 2σ 2 (1 + 3θ ) действительно обеспечивает несмещенность оценки θ .

2.1.3. Некорректность операции дифференцирования экспериментальных функций

В предыдущем разделе были рассмотрены алгоритмы решения об- ратных задач, основанные на конечно-разностной аппроксимации диффе- ренциальных уравнений. Этот подход следует применять с большой осто- рожностью, поскольку конечно-разностная аппроксимация эквивалентна непосредственному дифференцированию экспериментальных функций, чреватому большими погрешностями [4–6].

Проиллюстрируем это обстоятельство следующим простым приме-

ром.

Пусть дано уравнение

du	+ θ (u − 1) = 0 .	(2.13)
dt

vk.com/club152685050 | vk.com/id446425943

	Глава 2				95
Требуется определить параметр θ по замерам				yi	= u(ti ) + ε i , произ-
веденным в дискретные моменты времени			ti = i∆t	(i = 1,2,...,l) . Заменяя
производную конечно-разностной аппроксимацией				du	≈	yi +1 − yi	, полу-
				dt
чим из (2.13)						∆t

(i+1)		yi+1 − yi
θ	=		,		(2.14)
		(1− yi )∆t

(i+1)

где θ – оценка параметра θ , полученная после (i+1)-го замера.

Легко показать, что предложенный алгоритм неустойчив. Действи- тельно, по формуле Тейлора, имеем

u(ti +1 ) = u(ti )+ u′(ti )∆t + u′′(ti )

(∆t)2

+ o(∆t)2 ,

откуда

yi +1 − yi

− u′(ti

) ≈

εi +1 − εi

+ u′′(ti )

∆ t .

∆ t

Для относительной погрешности определения производной u′(ti ) по-

лучим выражение

δ u′

θ δ u′

≤

2ε

u′′

∆ t

(2.15)

u′

∆ t

1 − u 1 − u

где ε – абсолютная ошибка величины u.

Так как в первом слагаемом правой части (2.15) величина ∆t

стоит в

знаменателе, то ясно, что при малых ∆t дифференцирование эксперимен- тальных функций является неустойчивой операцией: малые погрешно- сти ε приводят к большим ошибкам в определении u′ .

Процедуру вычисления u′ можно регуляризовать, увеличивая про- межуток времени между замерами ∆t . Однако при этом увеличивается ошибка, допускаемая при конечно-разностной аппроксимации производ-

ной.

Минимальная ошибка, согласно (2.15), достигается при

2ε

u′′

∆t

δ u′ ≈

∆t

или ∆t = 2

. При таком значении ∆t

u′′ ε

u′′

u′

1 − u

Рассмотрим следующий математический эксперимент. В качестве

замеров yi

возьмем «зашумленные» значения решения уравнения (2.13)

при θ = 1 и начальном условии u(0) = 0 :

yi = 1 − e−ti + εi ,

εi

≤ 0,01,

(2.16)

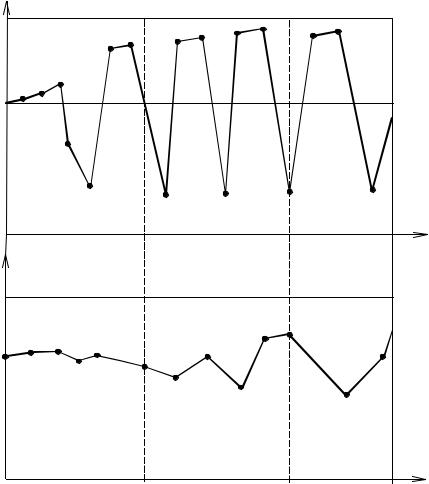
vk.com/club152685050 \| vk.com/id446425943
96	Глава 2
и используем их для оценки величины θ по формуле (2.14). Считая u ~ 0,5,
u′′ = e−t ~ 0,5 , получим,	что оптимальное значение ∆t			в этих условиях
равно 0,2. На рис. 2.1. приведены оценки величины θ			для разных момен-
тов времени при ∆t =0,02 и ∆t =0,2 (см. рис. 2.1, а и б соответственно).
θ
1,0
		а)
0,5				t
				t
θ
0,9
		б)
0,4	1	2		t
	1	2		t

Рис. 2.1. Оценки величины θ для разных моментов времени при ∆t =0,02 и ∆t =0,2

Как видим, при ∆t =0,02 проявляется неустойчивость решения об- ратной задачи. Увеличение промежутка времени между замерами до ∆t =0,2 устраняет неустойчивость при t ≤ 1, но приводит к смещению

оценки на 10%. При t > 1 неустойчивость появляется за счет уменьшения величины 1–u.

Операция интегрирования, являясь обратной операции дифференци- рования, в отношении воздействия на погрешности обладает также проти- воположными свойствами: при интегрировании погрешности эксперимен- тальных функций сглаживаются. В ряде случаев, подвергая дифференци- альное уравнение различным интегральным преобразованиям, можно по- лучить выражения, в которых будут отсутствовать производные экспери-

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 369 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
21.08.2019452.81 Кб3ПРОЕКТНЫХ РЕШЕНИЙ ПРИ РАЗРАБОТКЕ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ.pdf
#
15.09.2019315.6 Кб11Производство, хранение и выдача сжиженного природного газа.pdf
#
10.08.2019638.81 Кб28Происхождение нефти и газа.pdf
#
21.08.2019677.05 Кб6происхождения нефти и газа.pdf
#
16.08.2019226.07 Кб17Процессы и аппараты нефтегазопереработки и нефтехимического синтез.pdf
#
24.08.20198.3 Mб24ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ.pdf
#
10.08.2019220.54 Кб10развитие процессов нефтегазообразования и нефтегазонакопления.pdf
#
19.08.2019608.44 Кб12РАЗЛИВЫ НЕФТИ И НЕФТЕПРОДУКТОВ.pdf
#
17.08.2019955.13 Кб35Разработка нефтяных месторождений ответы.pdf
#
18.08.2019512.21 Кб11Разработка нефтяных месторождений.pdf
#
19.08.20193.99 Mб30РАЗРАБОТКИ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ.pdf