
ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ
.pdf
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 3 |
217 |
Учитывая условия (3.70), (3.82), (3.83), из (3.84), (3.85) получаем
∂ P (0, t) |
|
≤ |
∂P (0, t) |
≤ P |
n |
|
|
max |
|
|
|
|
|
|
a α Pn |
|
|
|
∂P (0, t) |
. |
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
∂ x |
|
|
σ |
|
F(σ )− |
|
1 |
|
|
c |
k |
2 |
(σ ) |
2 |
|
|
|
|
|||||||||||||||
|
∂ x |
|
|
|
|
|
|
|
c |
2 |
≤σ ≤σ |
|
|
|
|
|
|
|
a |
|
Pn |
|
|
|
|
∂ y |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|||||
Используя (3.84), (3.85), окончательно находим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
2 |
m |
2 |
|
|
≤ |
|
|
|
|
|
|||
|
|
|
|
(Pn+ 2 − Pn+ 2 )l−1P−n−1 1+ 2 |
∑ exp − π |
|
|
|
A1t |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
k |
|
c |
|
|
|
|
|
c |
|
|
|
|
m=1 |
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.86) |
|||||
|
∂P(0, t) |
≤ B(Pn |
|
|
− Pn+ 2 )l−1P−n−1 |
|
|
|
|
|
∞ |
|
|
|
|
|
2 |
2 |
t |
|
|
||||||||||||||||||||
≤ |
+ 2 |
+ |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
∑ exp − π |
|
m |
, |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
k |
|
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
m=1 |
|
|
|
A l2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|||||||
B |
|
min |
|
|
|
F(σ )− a1αPcn |
k2 (σ ) = |
|
max |
|
F(σ )− a1αPcn k2 |
(σ ) . |
|
||||||||||||||||||||||||||||
σ |
2 |
≤σ ≤σ |
|
|
a |
Pn |
|
|
|
|
σ |
2 |
≤σ ≤σ |
|
|
|
|
|
|
a |
Pn |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
k |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
k |
|
|
|
|
|
|
||||
Рассмотрим теперь случай, когда α < 0. |
Аналогично предыдущему |
||||||||||||||||||||||||||||||||||||||||
имеем P′(x, t) |
≤ P(x, t)≤ P′′(x, t) |
, |
где функции |
|
P′(x, t) |
|
|
и |
P′′(x, t) |
являются, |
|||||||||||||||||||||||||||||||
соответственно, решениями уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
∂ |
|
|
|
|
a α P |
|
|
|
|
∂(P′)2 |
|
|
a |
|
(1+ |
ασ ) ∂(P′)2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
F(σ )− |
|
1 |
|
|
c |
k |
2 |
(σ ) |
|
|
|
|
|
− |
|
1 |
P′ |
|
|
|
|
|
|
, |
|
|
|
|
||||||
|
|
|
|
∂ x |
|
|
|
∂ x |
|
|
|
|
|
∂ t |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
a |
2 |
P′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
a |
α P |
|
|
|
|
∂(P′′)2 |
|
|
a |
(1+ α σ ) |
∂(P′′)2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
F(σ )− |
1 |
|
|
k |
k |
2 |
(σ ) |
|
|
|
|
|
= |
1 |
P′′ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
∂ x |
|
|
|
∂ x |
|
|
|
|
|
∂ t |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
P′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и удовлетворяют условиям (3.72). При этом предполагается, что 1+ α σ > 0. Условия (3.70) в данном случае выполняются, что легко проверяется непо- средственно.
Повторяя те же рассуждения, что и в случае σ > 0 , приходим к сле- дующим результатам.
Нижняя и верхняя функции для P2 (x, t) имеют вид |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
+ (P2 |
− P2 ) |
|
|
2 |
|
|
∞ |
|
1 |
|
|
π |
2 |
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
P2 (x,t) = P2 |
|
x |
+ |
|
∑ |
exp − |
|
|
B1t |
sin |
π m x |
, |
|||||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
l2 |
||||||||||||||||||||||||||||||||||||
1 |
|
c |
|
k |
|
|
|
c |
|
l |
|
m=1 |
m |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
∞ |
|
1 |
|
|
π |
2 |
m |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
P2 |
(y, t) = P |
2 + (P |
2 + P |
2 ) |
y |
|
+ |
∑ |
exp |
− |
|
|
t sin π m y |
, |
|
||||||||||||||||||||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2 |
|
c |
k |
|
c l2 |
|
|
m=1 |
m |
|
|
B l |
2 |
|
|
|
l2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
y = x |
F(σ )− a1α Pk k |
2 |
(σ ) −1dx , |
|
|
|
|
l |
2 |
= |
|
max |
|
F(σ ) |
− |
a1αPk |
k |
2 |
(σ ) l , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∫ |
|
|
a2Pc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 ≤σ ≤σ 1 |
|
|
|
|
|
|
|
|
|
|
a2Pc |
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
B = P |
max |
a−1(1+ ασ )−1[F(σ )− a a |
−1αk |
|
(σ )] |
, |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
1 |
k σ |
≤σ ≤σ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
B |
= a P−1 |
2max |
1 [(1+ ασ )(F(σ )− a a −1αP P |
−1k |
|
|
(ασ ))] . |
|
|
|
|||||||||||||||||||||||||||||||
|
|
2 |
1 c |
σ 2 ≤σ ≤σ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
k c |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
vk.com/club152685050 | vk.com/id446425943
218 ГЛАВА 3
Для величины ∂P(0,t) |
получаем оценки |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 − P |
2 |
|
∞ |
|
π 2m2B t |
|
∂ P (0, t) |
|
P2 |
− P2 |
|
||||||||||||
|
k |
c |
1+ |
|
|
|
|
|
1 |
|
≤ |
|
|
|
≤ |
k |
|
|
c |
, |
|
|||
|
|
|
|
2 ∑ exp − |
|
l2 |
|
|
|
|
∂ x |
|
2l Pc |
|
|
|||||||||
|
2l Pc |
m=1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
max |
|
[F(σ )− a1a2−1αPk Pc−1k2 |
(σ )] |
|
|
|
|
∞ |
|
|
|
2 |
|
2 |
|
(3.87) |
|||||||
|
σ 2 ≤σ ≤σ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− π |
m |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
+ 2 |
∑ exp |
|
|
t . |
|||||||||
|
|
[F(σ ) |
− a a−1αP P−1k |
|
(σ )] |
|
|
|
||||||||||||||||
|
min |
|
2 |
|
|
|
m=1 |
|
|
B l2 |
|
|||||||||||||
|
σ 2 ≤σ ≤σ 1 |
|
|
1 2 |
k c |
|
|
|
|
|
|
|
|
|
2 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В качестве примера рассмотрим случай µ1 = 0.05µ2 , s = c , σ1 = 0,96 . |
||||||||||||||||||||||||
Для фазовых проницаемостей примем |
|
(σ ) = σ 4 . |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
k = (1− σ )3(1+ 3σ ), |
|
|
k |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При Pk = 1,1 Pc |
величина |
насыщенности |
σ |
изменяется |
в преде- |
|||||||||||||||||||
лах 0,94 < σ < 0,96 . Максимальная |
погрешность оценок |
(3.86) |
составля- |
|||||||||||||||||||||
ет 3%. При Pk |
= 1,2 Pc , соответственно, имеем 0,94 < σ < 0,96 , погрешность |
|||||||||||||||||||||||
равна 6%.
Следует отметить, что если известны значения функции σ (x, t) при x = 0 , то легко получить оценки более точные, чем (3.86), (3.87).
3.8.Периодические и стохастические автоколебания
вротационных вискозиметрах
Опыт реологии тиксотропных сред показывает, что в ряде случаев экспериментальное определение их реологических параметров затрудняет- ся невозможностью поддержания стационарных режимов течения. Так, при постоянном числе оборотов двигателя вискозиметра величина измеряемого касательного напряжения может меняться во времени достаточно сложным образом. Качественное описание этого эффекта приведено в [55]. Анало- гичные осложнения возможны и в случае капиллярного вискозиметра, что,
вчастности, подтверждается опытами по исследованию колебательных режимов истечения полимерных растворов из капилляра [56]. Это явление
внаучной литературе получило название эластичной турбулентности.
Для его объяснения привлекалась гипотеза проскальзывания жидкости у стенок вискозиметра или капилляра [57–59]. Высказывалось также предпо-
ложение о том, что причиной возникновения эластичной турбулентности являются происходящие в процессе течения структурные перестройки [60].
Рассмотрим математическую модель, описывающую движение тик- сотропной жидкости в зазоре между цилиндрами ротационного вискози- метра. Считая толщину зазора малой по сравнению с радиусами цилинд- ров, примем плоскую схему течения, согласно которой исследуемая жид-
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 3 |
219 |
кость находится между двумя параллельными пластинами, отстоящими друг от друга на расстоянии h .
Нижняя бесконечно протяженная пластина неподвижна, а верхняя – подвижная – обладает достаточно большой площадью, чтобы можно было бы пренебречь краевыми эффектами. Верхняя пластина приводится в по- ступательное движение с помощью пружины, один конец которой прикре- плен к пластине, а другой движется с постоянной скоростью υ0 .
Сдвиговое течение жидкости между пластинами описывается урав- нением
|
|
∂ υ |
|
|
∂ |
|
|
|
|
|
|
|
|
ρ |
= |
|
|
µ ∂ υ , |
0 < y < h , |
(3.88) |
|||||
|
∂ t |
∂ |
|
|||||||||
|
|
|
|
y |
∂ y |
|
|
|||||
где υ , |
ρ , µ – соответственно скорость, плотность и вязкость жидкости, |
|||||||||||
y – расстояние от нижней пластины. |
|
|
|
|
||||||||
Уравнение движения верхней пластины имеет вид |
|
|||||||||||
|
m |
d 2 x |
− Qµ |
∂ υ |
|
|
+ fx = 0 , |
(3.89) |
||||
|
|
|
||||||||||
|
dt2 |
|
∂ y |
|
|
|||||||
|
|
|
|
|
|
|
|
y=h |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
где x |
– абсолютное удлинение пружины, |
f – коэффициент ее жесткости, |
||||||||||
m, Q – масса и площадь верхней пластины.
Система уравнений (3.88), (3.89) замыкается с помощью граничных
условий вида |
|
|
|
υ (0, t) = 0, |
υ (h,t) = υ0 |
− dx . |
(3.90) |
|
|
dt |
|
Вязкость тиксотропной жидкости зависит от степени ее структури- рованности. В качестве количественной характеристики степени структу- рированности жидкости будем использовать концентрацию разрушенных в процессе течения связей s . Зависимость вязкости жидкости от концентра- ции s примем в виде
µ (s) = |
exp(− σsβ )− exp(− σsβ ) |
|
1 |
− exp(− σsβ ) |
|
|
1− exp(− σsβ ) |
|
µ0 + |
1 |
− exp(− σsβ )µ , |
(3.91) |
|
|
|
|
|
|
|
|
где σ , β – некоторые положительные постоянные.
В соответствии с этой параметризацией при s = 0 вязкость жидкости максимальна и равна µ0 . По мере разрушения связей (с увеличением s ) вязкость уменьшается по нелинейно-экспоненциальному закону, достигая своего минимального значения µ при s = s .
Для описания процессов разрушения–восстановления связей между структурными элементами среды при сдвиговом течении введем следую- щее кинетическое уравнение:
∂ s = −α {s − s [1− exp(− γsµ (s)ε&2 )]}, (3.92)
∂ t
где α и γ – положительные постоянные, ε& = ∂ υ 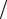 ∂ y – скорость сдвига.
∂ y – скорость сдвига.



vk.com/club152685050 | vk.com/id446425943 |
|
||
222 |
ГЛАВА 3 |
|
|
разрушения поля течения на доменные структуры. Если в начальный мо- |
|||
мент времени по каким-либо причинам часть структурных связей наруше- |
|||
на, т. е. Si (0) ≠ 0, |
то эти разрушенные связи со временем полностью вос- |
||
станавливаются. |
|
|
|
Т |
|
|
|
0,45 |
|
|
|
0,22 |
|
|
|
0,00 |
0,82 |
1,63 |
& |
|
|
|
E |
|
Рис. 3.11. |
& |
|
|
Зависимость Т от E |
|
|
С увеличением скорости сдвига ( E& > 0,95) происходит разделение поля течения на «доменные» структуры с разрушением части связей вбли- зи подвижной стенки. При этом нулевое состояние Si = 0 теряет устойчи- вость с рождением нового положения равновесия Si ≠ 0, которое, в свою
очередь, при дальнейшем увеличении E& теряет устойчивость с образова- нием предельного цикла. Размах колебаний величины касательного напряжения (Tmax и Tmin ) показан на рис. 3.11 пунктирными линиями. Средние по времени значения Т при этих колебаниях изображены тонкой сплошной линией.
При дальнейшем увеличении скорости сдвига E& имеет место про- цесс последовательного удвоения периода автоколебаний, приводящий к хаосу при E& = E&∞ = 1,517. Наблюдающиеся при этом стохастические коле-
бания величины касательного напряжения показаны на рис. 3.12.
Анализ соответствующего этому аттрактору отображения Лоренца (связи между последовательными экстремумами напряжения, рис. 3.13) показывает, что в исследуемой системе переход к хаосу реализуется по
vk.com/club152685050 | vk.com/id446425943 |
|
|
|
|
||
|
|
ГЛАВА 3 |
|
|
223 |
|
классическому сценарию Фейгенбаума. Об этом свидетельствует также то, |
||||||
что значения параметра |
& 2 |
|
|
|
|
|
En , при которых происходит удвоение периода, |
||||||
подчиняются закону Фейгенбаума: |
|
|
|
|
||
|
G |
− G |
= C |
, |
|
|
|
n |
∞ |
δ n |
|
|
|
где в данном случае С = 6,54. |
|
|
|
|
||
|
|
|
|
|
||
Т |
|
|
|
|
|
|
0,41 |
|
|
|
|
|
|
0,27 |
|
|
|
|
|
|
0,14 |
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
0,0 |
7,2 |
14,4 |
|
21,6 |
28,8 |
τ |
Рис. 3.12. Хаотические колебания касательного напряжения |
||||||
S(n+1) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1,78 |
|
|
|
|
|
|
1,45 |
|
|
|
|
|
|
1,13 |
|
|
|
|
|
|
1,13 |
|
1,45 |
|
1,78 |
|
(n) |
|
|
|
|
|
|
S1 |
|
Рис. 3.13. Одномерное отображение |
|
|
|||
vk.com/club152685050 | vk.com/id446425943
224 ГЛАВА 3
Для существования стохастического поведения необходимо выпол- нение условия размешивания, что обеспечивается экспоненциальным раз- беганием траекторий в каждой точке аттрактора (см. главу 1). Характер этого разбегания можно оценить, исследуя энтропию Колмогорова, кото- рая определяется выражением [40, 62]
K = |
1 |
|
R(τ ) |
τ |
ln |
R(0) , |
где R(0) и R(τ) – расстояния между двумя точками в фазовом пространстве, соответственно, в начальный момент времени и через промежуток време- ни, равный τ .
K
0,1
K∞=0,057
0
0,44 |
19,33 |
38,22 |
57,11 |
τ |
|
Рис. 3.14. Энтропия Колмогорова |
|
||
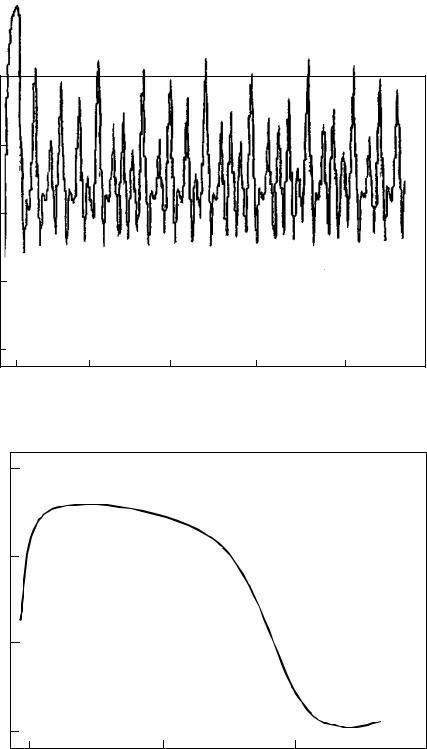
Зависимость энтропии Колмогорова от τ показана на рис. 3.14. Для |
||||
стохастического |
процесса при |
τ → ∞ величина энтропии должна быть |
||
больше нуля. Из рис 3.14 видно, что со временем величина энтропии Кол- могорова выходит на положительный стационарный уровень K∞ = 0,057.
При дальнейшем увеличении скорости сдвига ( E& > 1,67) имеет место обратный каскад бифуркаций Фейгенбаума, который при значе- нии E = 1,87 приводит к исчезновению автоколебаний с образованием ус- тойчивого равновесия. Это равновесие характеризуется высокой степенью разрушения структурных связей ближнего к подвижной стенке «домена». С увеличением E& число этих разрушенных связей возрастает, асимптоти- чески стремясь к своему максимальному значению.
vk.com/club152685050 | vk.com/id446425943
ГЛАВА 3 |
225 |
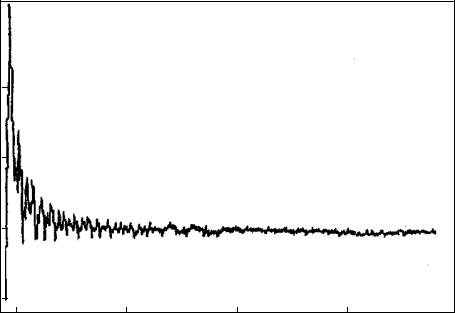
Для подтверждения полученных результатов рассмотрим результаты вискозиметрических экспериментов, проведенных С. А. Коневым с рас- плавом парафина (нонодекан). Оказалось, что при температурах, близких к температуре кристаллизации парафина, значения касательного напряже-
ния τ испытывают незатухающие колебания, график которых представлен на рис. 3.15. Для этой кривой нами были вычислены корреляционная раз-
мерность ν (см. главу 1) и энтропия Колмогорова. Результаты расчетов корреляционной размерности приведены на рис. 3.16, из которого видно, что наблюдаемые хаотические колебания являются детерминированными, причем число динамических переменных, необходимых для описания рас- сматриваемого процесса, равно 4. Отметим, что вышеприведенные чис- ленные результаты были получены нами при анализе динамической систе- мы, которая также имеет четвертый порядок.
τ
144
96
48
0
0 |
21,1 |
42,2 |
63,3 |
84,4 |
t, с |
Рис. 3.15. Замеры касательного напряжения
Оценка снизу для энтропии Колмогорова вычислялась по форму-
ле [62]
|
Cn (r) |
||
K = lim lim ln |
|
|
|
|
|||
r→∞ n→∞ |
Cn (0) |
||
и оказалась равной K = 0,1, что по порядку совпадает со значением, соот- ветствующим модельной системе. Здесь Cn (r) – корреляционный интеграл (см. раздел 1.4).
Полученные нами результаты позволяют по-новому взглянуть на эффект эластичной турбулентностии и могут быть полезными при разра- ботке нетрадиционных методов обработки данных реометрических экспе- риментов.

vk.com/club152685050 | vk.com/id446425943 |
|
|
|
||
226 |
|
ГЛАВА 3 |
|
|
|
ln с |
|
|
|
|
|
-1,77 |
|
|
|
|
|
|
|
ν |
|
|
|
|
|
3,23 |
|
|
|
-3,55 |
|
|
|
|
|
|
|
1,85 1 |
3 |
5 |
m |
|
|
ε |
|
|
|
-5,32 |
|
ln |
|
|
|
|
|
|
|
|
|
-1,67 |
-0,70 |
-0,28 |
1,26 |
|
|
Рис. 3.16. Вычисление корреляционной зависимости |
|
||||
3.9. Исследование устойчивости работы штангового насоса
При откачке маловязких жидкостей штанговым глубинным насосом возникают колебания колонны штанг, приводящие к резкому увеличению инерционных нагрузок на штангу и возникновению пульсаций давления в скважине.
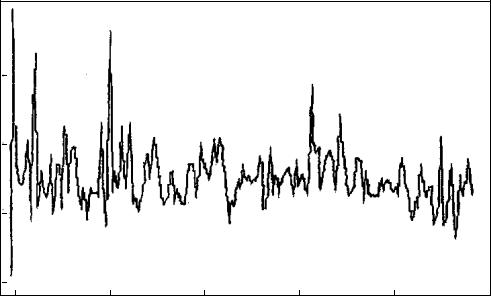
Для исследования этих эффектов были проведены промысловые ис- пытания [63], в ходе которых осуществлялась запись давления P(t) при
работе штангового насоса в скважине № 116 НГДУ «Аксаковнефть»
(рис. 3.17).
Запись производилась с помощью дистанционных тензометрических датчиков давления, электронного потенциометра Н-135 и дублирующего его шлейфового осциллографа. Жидкость перекачивалась по замкнутому циклу: насос – НКТ – затрубное пространство – насос. Рабочими жидко- стями были пластовая вода (вязкость ≈1,0 мПа с), дегазированная нефть
с вязкостью ≈ 0,05 Па с и эмульсия с водосодержанием 64,5%, эффек-
тивная вязкость которой в рабочей зоне градиента сдвига составля- ла ≈ 0,54 Па с.
Из рис. 3.17 видно, что откачка воды сопровождается хаотическим изменением давления жидкости в НКТ. С увеличением вязкости жидкости пульсации давления уменьшаются. Откачка эмульсии происходит без пульсаций давления, что свидетельствует о полном затухании вибрации штанг под действием вязкого трения.


