ПРОЦЕССЫ НЕФТЕГАЗОДОБЫЧИ

vk.com/club152685050 | vk.com/id446425943

198 ГЛАВА 3

Из этого решения следует, что падение давления в скважине после мгновенной закачки некоторой порции жидкости происходит по зако-

ну pc t11−v . Спрямляя кривую падения давления в координатах ln p–ln t,

можно по углу наклона прямой определить величину v .

где k – проницаемость, h – толщина пласта.

Вместо (3.44) при этом получается соотношение [34, 35]

Ψ(s) = b + f ln 1 ,

s

Таким образом, в случае фильтрации на фрактале кривая изменения

плоскорадиальной фильтрации в евклидовом пространстве – в координатах

может свидетельствовать о необходимости проведения мероприятий, на- правленных на разрушение фрактальной структуры. Поэтому при выборе скважин, подлежащих воздействию, целесообразно учесть также результа- ты обработки кривых изменения давления по изложенной выше методике.

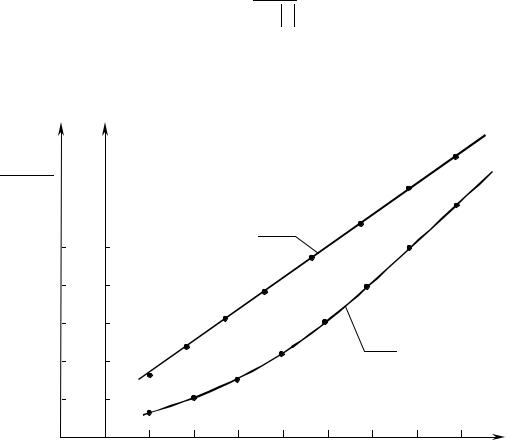
Для примера на рис. 3.6 и 3.7 представлены КВД, снятые в скважи- не № 151 Манчаровского нефтяного месторождения (НГДУ «Чекмагуш- нефть»), соответственно, до и после проведения термогазохимического

Рис. 3.6. КВД, снятая в скважине № 151 Манчаровского нефтяного месторождения (НГДУ «Чекмагушнефть»)

до воздействия ТХГВ:

vk.com/club152685050 | vk.com/id446425943

200 ГЛАВА 3

3.5. О колебаниях расхода при фильтрации полимерных растворов

Нелинейные эффекты при фильтрации неньютоновских сред могут привести к потере устойчивости стационарного режима фильтрации [36– 39]. Подобные явления наблюдались нами в ряде лабораторных экспери- ментов, в которых изучалась фильтрация растворов полиакриламида (ПАА) через колонку, набитую кварцевым песком. Проницаемость порис-

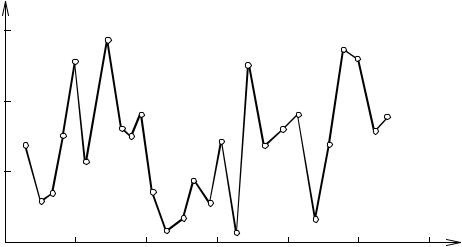
той среды по воздуху составляла 3,1 10−12 м2. В ходе экспериментов дав- ления на входе и выходе колонки поддерживались постоянными и в тече- ние достаточно долгого времени замерялся расход фильтрующейся жидко- сти. Опыты показали, что при малых перепадах давления устанавливается стационарное значение расхода. Но при достижении некоторого критиче- ского перепада давления ∆p (зависящего от концентрации ПАА в раство- ре) стационарные режимы фильтрации теряют устойчивость, наблюдаются незатухающие колебания расхода Q(t). Для примера на рис. 3.8 представ-

vk.com/club152685050 | vk.com/id446425943

лена зависимость расхода раствора ПАА концентрации 0,075% от времени при ∆p = 0,6 МПа.

Q 10-5,

м3/с

0,8

0,6

Рис. 3.8. Зависимость расхода раствора ПАА от времени

Колебания расхода имеют нерегулярный характер. Степень нерегу- лярности (хаотичности) можно оценить по размерности Хаусдорфа для графика Q = Q(t) . Величина D определяется (см. главу 1) в процессе изме- рения длины l кривой Q = Q(t) с помощью циркуля с раствором ε . В ходе измерения начинают с исходной точки P0 . Описав окружность радиусом ε с центром в P0 , отмечают точку первого выхода кривой из круга P1. Вто-

дет l = liml(ε ) .

ε →0

Как показывают непосредственные изменения, l(ε ) ~ ε −γ для экспе- риментальных кривых Q = Q(t) при не слишком малых ε . Следовательно, графики функций Q = Q(t) можно считать фрактальными кривыми с раз- мерностью D = γ +1. Естественно предположить, что чем больше размер- ность экспериментальной кривой, тем менее упорядочен процесс, отобра- жением которого является эта кривая. Нужно отметить тот факт, что после установления хаотического режима фильтрации дальнейшее увеличение перепада давления приводит не к увеличению, а к уменьшению размерно- сти Хаусдорфа кривых Q = Q(t) , что свидетельствует о более упорядочен-

ном протекании процесса фильтрации при больших значениях величи- ны ∆p .

vk.com/club152685050 | vk.com/id446425943

υ = υ1 = (B − 1)1/ N . Дальнейшее увеличение параметра В приводит к тому, что в критической точке B = B0 стационарный режим фильтрации со ско- ростью υ = υ1 также становится неустойчивым. В системе возникают пе-

определяется из уравнения τ = −η ctgη, π2 < η < π .

Приведем некоторые количественные оценки. Время пьезопроводно-

L2

сти λ имеет порядок χ , где χ – коэффициент пьезопроводности. Эту ве-

личину определяли по кривым восстановления давления, снятым предва- рительно на колонке. Было получено λ ~ 0,5 − 1 мин. Время запаздывания Т зависит от концентрации полимера и меняется от 5–10 мин до 1–2 ч [26]. Для полимерных растворов, использованных в наших экспериментах, можно принять Т ~ 5 мин. Считая, что λ ~ 1 мин, получаем оценку τ ≈ 5.

оценок величины N у нас нет необходимых данных, но тот факт, что поте- ря устойчивости стационарной фильтрации полимерных растворов наблю- далась экспериментально, является косвенным свидетельством того, что величина N достаточно велика (при τ = 5, по крайней мере, N > 2,1).

Выбор функции c(υ) в виде (3.47) предполагает, что при увеличении скорости фильтрации величина с стремится к нулю. Более общим является случай, когда коэффициент фильтрации при больших υ стремится к неко- торому асимптотическому значению, отличному от нуля. Поэтому нами проведены расчеты с функцией c(υ) вида

результатов относительно смены способа параметризации функции c(υ).

vk.com/club152685050 | vk.com/id446425943

204 ГЛАВА 3

Расчеты показали, что эффекты возникновения периодических и сто- хастических автоколебаний имеют место и в этом случае. Приведем здесь результаты, полученные при А = 10, G = 2, N = 5, τ = 5. Вначале увеличе-

ние параметра В ведет через цепь бифуркаций удвоения периода в точках B1 ≈ 1,20 ; B2 ≈ 1,46 ; B3 ≈ 1,60 ; … к установлению хаотического режима.

Дальнейшее увеличение В приводит к тому, что движение в системе упо- рядочивается. Возникают предельные циклы, периоды которых по мере роста В последовательно уменьшаются вдвое, т. е. возникают обратные бифуркации Фейгенбаума [42]. Наконец, при некотором достаточно боль- шом значении B вновь устанавливается стационарное состояние.

Обратный переход от хаоса к стационарному состоянию, обнаружен- ный при исследовании предложенной модели, может послужить объясне- нием тому факту, что увеличение перепада давления приводит к уменьше- нию нерегулярности зависимостей Q = Q(t).

Таким образом, нами показано, что колебания расхода при фильтра- ции полимерных растворов можно объяснить тремя причинами: наличием начального градиента давления, эффектом «запирания» потока клубками полимерных молекул и существованием некоторого времени запаздывания в процессах структурных преобразований в полимерных системах. Качест- венные выводы, сделанные из анализа предложенной модели, находятся в соответствии с экспериментально полученными результатами.

Данные результаты могут найти широкое применение при разработ- ке стратегии управления закачкой растворов полимеров в нефтеносные пласты. Они позволяют, в частности, назначить режимы закачки, исклю- чающие возникновение хаотических колебаний.

3.6. О фильтрационных характеристиках с учетом сорбционной способности

Стационарное движение газа в пористых средах может быть описано различными законами фильтрации: линейным (законом Дарси), двучлен- ным, с начальным градиентом давления. При экспериментальном опреде- лении вида закона фильтрации обычно используют данные стационарных исследований, изменяя значения перепада давления и дожидаясь установ- ления стационарных значений расходов, соответствующих данным пере- падам давления. Время, необходимое для установления стационарного ре- жима фильтрации, определяют из гидродинамических соображений. Одна- ко в определенных условиях стабилизация фильтрационного потока может происходить в течение длительного времени, многократно превышающего гидродинамическое время. В частности, к «затягиванию» процесса уста- новления стационарной фильтрации могут привести медленные сорбцион-

vk.com/club152685050 | vk.com/id446425943

ные процессы. Это необходимо учитывать при обработке эксперименталь- ных данных [43].

Влияние сорбированного газа на фильтрационные характеристики может быть весьма ощутимым. Дело в том, что при проведении исследова- ний по определению фильтрационных свойств за время исследований че- рез модель проходит объем газа, составляющий незначительную часть от объема газа, заключенного в порах, причем с увеличением размеров моде- ли эта величина уменьшается. Так, например, простой расчет показывает, что время, необходимое для фильтрации через модель одного порового объема газа при проницаемости ~10–15 м2, длине модели L ~ 10 м, перепаде давления∆P ~ 0,1 МПа и давлении в модели Р ~ 1 МПа, имеет величину порядка суток и более. Поэтому массообмен между сорбированным и сво- бодным газом может ощутимо влиять на характеристику фильтрационного протока.

Сорбция (соответственно десорбция) газа происходит весьма мед- ленно. Оценки показывают, что характерные времена этих процессов для лабораторных экспериментов составляют не менее 104 с. Следует, однако, учитывать наличие как поверхностной, так и объемной сорбции, т. е. диф- фузию молекул газа внутрь зерен породы. Известно, что среднее время трехмерной диффузии значительно больше, чем двухмерной при одинако- вых геометрических размерах (например, диффузия в шаре и круге одного радиуса). Поэтому стабилизация сорбционного, а следовательно, и гидро- динамического режима происходит в течение времени, значительно пре- вышающего реальные времена наблюдений при проведении эксперимен- тов. Исходя из этого, ниже рассматривается модель фильтрации газа с уче- том кинетики сорбции в изотермических условиях.

Система уравнений линейной фильтрации газа с учетом сорбционно- го обмена имеет обычный вид:

где m – пористость, ρ – плотность, υ – скорость фильтрации, k – прони- цаемость, – вязкость, Р – давление, f – член, характеризующий сорбци- онный массообмен.

Процесс сорбции газа породой можно рассматривать как двухэтап- ный – осаждение молекул на поверхности и диффузия внутрь блока зерен породы. Поскольку диффузионный процесс, как более медленный, являет- ся лимитирующим этапом, можно рассматривать сорбцию газа как диффу- зию внутрь зерен породы, а кинетику поверхностной сорбции учитывать в граничных условиях.

Для расчета диффузии молекул газа в твердом теле необходимо вы- брать определенную модель. В дальнейшем будет использоваться одно- мерное уравнение диффузии (нетрудно показать, что при использовании