Пружинный маятник (рис. 3)

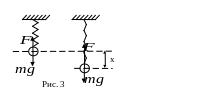
Применим к движению груза на пружине второй закон Ньютона: , где - сила упругости: ,

. (6)

Сравнивая (5) и (6), получаем:

(7)

(8)

Мы нашли собственную циклическую частоту (7) и период колебаний (8) груза на пружине.

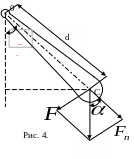
Физический маятник (рис. 4)

Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения ( -мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке :

Момент этой силы относительно оси равен:

, где - плечо силы относительно оси , знак минус соответствует тому, что момент стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе.

В соответствии с уравнением динамики вращательного движения

, где - угловое ускорение, - момент инерции маятника относительно оси О. Получаем

. (9)

Ограничившись малыми колебаниями , после преобразований получаем уравнение (9) в виде:

(10).

Сравнив выражения (5) и (10) мы видим их математическую аналогию, что позволяет записать выражения для циклической частоты и периода колебаний физического маятника:

(11)

, (12)

где -расстояние от центра тяжести до оси вращения.

Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах.

Математический маятник (рис. 5)

М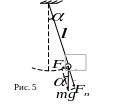 атематический маятник является частным случаем физического маятника. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, к которой подвешена масса, сосредоточенная в одной точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника ,где -длина математического маятника. Тогда формулы (11) и (12) запишутся в виде:

(13)

(14)

Сравнивая формулы (12) и (14), заключаем, что физический маятник колеблется с периодом математического маятника, длина которого

,

называется приведенной длиной физического маятника.

Гармонический осциллятор при наличии сил сопротивления

Как уже отмечалось, затухающие колебания возникают при наличии сил сопротивления (трения) и обусловлены рассеянием (диссипацией) энергии. Если убыль энергии не восполняется за счёт работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем, наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:

, (15)

где - постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила сопротивления и скорость имеют противоположные направления, следовательно, их проекции на ось имеют разные знаки.

Запишем уравнение второго закона Ньютона для движения груза на пружине при наличии сил сопротивления:

. (16)

Введя обозначения: , получим однородное дифференциальное уравнение затухающих колебаний:

, (17)

где - коэффициент затухания, - собственная частота колебаний, т.е. частота, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при ).

Решение уравнения (17) проведем через анализ рассеяния энергии. Для этого сначала найдем полную энергию гармонического осциллятора при отсутствии сил сопротивления. Подставив в выражение для кинетической энергии скорость осциллятора (3), получим:

. (18)

Потенциальная энергия упругой деформации после подстановки из формулы (1) имеет следующий вид:

. (19)

Выразив из формулы коэффициент и подставив его в (19), получим выражение для полной энергии гармонического осциллятора:

. (20)

Полная энергия гармонического осциллятора сохраняется в отсутствие сил сопротивления и пропорциональна квадрату амплитуды колебаний. Таким образом, процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние (за период колебаний) значения потенциальной и кинетической энергии одинаковы, и каждое из них равно .

Выясним, как влияют силы сопротивления на энергию колебательной системы (осциллятора). Будем при этом считать, что сила сопротивления настолько мала, что вызываемые ею потери энергии за один период относительно малы. Потеря энергии телом определится как работа, произведённая силой сопротивления. За время эта работа, а с ней и потеря энергии равна произведению силы сопротивления на смещение тела ( ):

,

откуда

. (21)

При сделанном нами предположении о малости сил сопротивления мы можем в (21) заменить кинетическую энергию половиной полной энергии осциллятора :

. (22)

Перепишем это выражение в виде:

.

Путем интегрирования находим, что , окончательно:

, (38)

где – значение энергии в начальный момент времени ( ).

Таким образом, энергия колебательной системы убывает из-за сил сопротивления по экспоненциальному закону. Вместе с энергией убывает и амплитуда колебаний. Поскольку энергия пропорциональна квадрату амплитуды, получаем

. (23)

Таким образом, при не слишком большом затухании общее решение уравнения (23) имеет вид:

. (24)

Здесь – значение амплитуды в начальный момент времени, - начальная фаза, - частота колебаний.

. (25)

На рисунке 6 дан график функции (24). Пунктирными линиями показаны пределы, в которых находится смеще­ние колеблю­щейся точки. В соответствии с видом функции (24) движение системы можно рассматри­вать как гармони­ческое колебание частоты с амплитудой, изменяющейся по закону, определяемому формулой (23). Верхняя из пунктирных кривых на рисунке 6 дает график функции A(t). Начальное смещение зависит кроме также от начальной фазы :

.

Степень убывания амплитуды определяется коэффициентом затухания. За время амплитуда уменьшается в раз - это время называется временем релаксации колебаний. Сделанное нами выше предположение о малости сил сопротивления означает, что предполагается большим по сравнению с периодом колебаний

, (26)

т.е. за время релаксации происходит большое число колебаний . Величину, обратную N_e называют логарифмическим декрементом затухания :

. (27)

Итак, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время релаксации. Кроме того, логарифмический декремент затухания часто определяют как натуральный логарифм отношения двух последующих амплитуд.

Для характеристики колебательной системы также вводят величину, называемую добротностью колебательной системы

. (28)

Из формулы (25) следует, что с ростом коэффициента затухания период колебаний увеличивается. При движение перестаёт быть периодическим, происходит срыв колебаний, или движение носит апериодический (непериодический) характер - выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.