Циркуляция вектора магнитного поля
Согласно теореме о циркуляции , можно записать
Используя связь , запишем
Таковы опытные факты, которые мы изучили.
Ток смещения
Мы
видели, что изменяющееся во времени
магнитное поле индуцирует вихревое
электрическое поле
.
Максвелл предположил, что и меняющееся
во времени электрическое поле индуцирует
вихревое магнитное поле
.
Причем закон их связи аналогичен
уравнению (VI)
Это свое предположение он обосновывал, изучая прохождение переменного тока через конденсатор. В самом деле, между обкладками конденсатора находится диэлектрик, т.е. изолятор. Постоянный ток через конденсатор не проходит, переменный ‑ проходит!
В переменном поле происходит лишь смещение связанных зарядов диэлектрика от положения равновесия в обе стороны и получается как бы прохождение тока, аналогично постоянному току.
Поэтому ток через конденсатор называют током смещения. Найдем выражение для плотности тока через конденсатор, т.е. для тока смещения.
Таким
образом ‑
.
С другой стороны, напряженность поля внутри конденсатора равна
Следовательно
‑
.
Максвелл предположил, что ток смещения обладает всеми свойствами тока проводимости и, в частности, создает магнитное поле
Тогда,
записывая, что плотность тока равна
сумме плотности тока проводимости и
плотности тока смещения ‑
,
циркуляцию магнитного поля можно
записать в виде
Обычно
никогда не пишут
или
,
а просто
и
.
Таким образом, окончательное выражение для циркуляции магнитного поля будет иметь вид
(VII)
Это ‑ последнее уравнение Максвелла в интегральной форме ‑ циркуляция вектора магнитного поля по замкнутому контуру равна сумме токов проводимости и токов смещения, охватываемых этим контуром.
Этому уравнению соответствует дифференциальная форма
(VII’)
Таким образом, мы получили все четыре уравнения Максвелла в интегральной форме:
Этим четырем уравнениям в интегральной форме соответствуют четыре уравнения в дифференциальной форме:
К этим четырем уравнениям добавляют еще три уравнения среды:
Эти уравнения образуют замкнутую систему уравнений электромагнитного поля и описывают все многообразие электромагнитных процессов известного нам реального мира. Так мы от опытных, частных законов ‑ закон Кулона, закон Био-Савара, закон э/м индукции ‑ пришли к обобщенным уравнениям электромагнитного поля.
Лекция 3. (2 часа)
Свободные незатухающие и затухающие механические колебания.
(Гармонические колебания и их характеристики. Свободные незатухающие механические колебания. Пружинный и математический маятники. Скорость и ускорение, кинетическая, потенциальная и полная энергия материальной точки, совершающей незатухающие колебания. Свободные затухающие механические колебания. Их уравнения и характеристики. Сложение колебаний.)
Общие сведения о колебаниях.
Одномерный классический гармонический осциллятор
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Рассмотрим механические колебания.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Силу, под действием которой происходит колебательный процесс, называют возвращающей силой, так как она стремится вернуть тело или материальную точку в положение равновесия.
Свободные колебания совершаются системой, выведенной из положения равновесия.
Собственными называются свободные колебания без учёта сил сопротивления (без затухания).
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счёт энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.
При параметрических колебаниях за счёт внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.
Простейшими
являются гармонические
колебания,
при которых колеблющаяся величина
(например, отклонение маятника) изменяется
со временем по закону синуса или косинуса.
Этот вид колебаний особенно важен по
следующим причинам: во-первых, колебания
в природе и в технике часто имеют
характер, очень близкий к гармоническому,
во-вторых, периодические процессы иной
формы (с другой зависимостью от времени)
могут быть представлены как наложение
нескольких гармонических колебаний.
Гармонические колебания удобно
представить в виде круговой диаграммы
(рис.1). Пусть точка
движется по окружности радиусом
.
Её положение задаётся радиус-вектором
.
Положение равновесия задаётся точкой
.
Радиус-вектор
равномерно вращается с угловой скоростью
.
Проекции радиус-вектора
на оси
или
задаются математическими выражениями
(уравнениями) гармонических колебаний:
(1)
(2)
М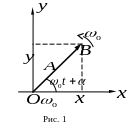
ы
будем использовать уравнение гармонических
колебаний в виде (1). Координата
задаёт значение колеблющейся величины.
Величина
– амплитуда
колебаний,
т.е. максимальное отклонение колеблющейся
точки от положения равновесия. Величина
,
равная числу колебаний за время
секунды, называется циклической
частотой.
Аргумент косинуса
,
характеризующий значение колеблющейся
величины в момент времени
,
называется фазой
колебаний.
Фаза колебаний
,
соответствующая начальному моменту
времени, называется начальной
фазой
колебаний. Время одного полного колебания
называется периодом
колебаний.
Число колебаний
за время, равное одной секунде, называется
частотой
колебаний.
.
Скорость колеблющейся точки находится дифференцированием выражения (1) по времени:
(3)
Дифференцируя вторично, получаем ускорение:
.
(4)
.
На
рис. 2 представлены зависимости
.
Скорость опережает смещение на
,
ускорение находится в противофазе по
отношению к смещению.
Каждое
конкретное колебание характеризуется
определенным значением амплитуды
и начальной фазы
.
Определим их значения из начальных
условий
.
В этом случае
,
.
Отсюда следует, что
,
.
Выведем дифференциальное уравнение гармонических колебаний. Из выражения (4) следует, что
или
. (5)
Уравнение (5) является дифференциальным уравнением гармонических колебаний. Это уравнение является общим уравнением, описывающим гармонические колебания. Его решением являются функции (1) или (2). Следовательно, можно сказать, что гармоническими называются колебания, совершаемые по закону синуса или косинуса.
Колебательные системы, описываемые уравнением (5) называются одномерным классическим гармоническим осциллятором. Модель одномерного классического гармонического осциллятора оказывается справедливой не только для механических, но и других видов собственных незатухающих колебаний. В различных разделах физики используется единый математический язык описания гармонических колебаний.
Рассмотрим конкретные примеры гармонических осцилляторов в механике.