Соотношение неопределенностей

Проанализируем теперь вопрос о точности определения координат и импульса различных тел.

Согласно гипотезе Луи-де-Бройля, все тела обладают волновыми свойствами, т.е. характеризуются волной, или, как принято говорить, описываются волновой функцией.

В общем случае волновая функция зависит от всех трех пространственных координат и времени . Волновую функцию обозначают символом . Итак

Рассмотрим простейший случай волновой функции, зависящей только от одной пространственной координаты ‑ и простейший вид волновой функции ‑ плоскую, монохроматическую волну:

Окончательно волновую функцию запишем в виде:

(3)

где ‑ длина волны, ‑ скорость ее распространения. Согласно гипотезе де-Бройля, .

Поскольку волна монохроматическая, то , отсюда и импульс постоянен . Т.е. импульс имеет строго определенное значение. Следовательно, изменение импульса ‑ интервал его возможных значений ‑ равен нулю. Значение импульса одно единственное и четко определено ‑ .

В то же время, рассматриваемая монохроматическая волна бесконечна, она не имеет ни начала, ни конца и заполняет все пространство . Следовательно, значение неопределенно и интервал возможных значений равен бесконечности. Итак

Т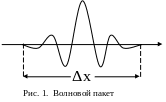 .е. такой объект как плоская монохроматическая волна имеет совершенно определенный импульс и совершенно неопределенную область локализации.

Рассмотрим теперь другой объект ‑ волновой пакет (см. рис. 1). Т.е. такую волну, которая отлична от нуля лишь в некотором интервале , а во всех остальных точках пространства равна нулю.

Такой волновой пакет можно получить, складывая монохроматические волны разных частот, т.е. разных длин волн, в некотором интервале от до . Следовательно, область локализации такого объекта уменьшилась и стала .

Посмотрим теперь, что стало с импульсом. А импульс стал неопределенен. Ведь импульс определяется через длину волны , а волновой пакет состоит из целой серии волн, разной длины. Поэтому импульс потерял свое определенное значение. Интервал возможных значений импульса заключен в пределах:

Чем более узкая область локализации пакета ‑ , тем более широкий диапазон длин волн должен быть для его реализации. В пределе, очевидно, получим:

Соотношение между и (аналогично и для других координат) впервые проанализировал Гейзенберг. Он исходил из следующего.

Чтобы определить положение и импульс электрона, его нужно осветить, т.е. получить от него хотя бы один рассеянный фотон. При этом, вследствие дифракции, точность в определении положения электрона не может быть больше длины волны фотона: . Чем точнее нужно измерить положение электрона, тем короче должна быть длина волны .

Но при рассеянии фотона электрон получает отдачу и его импульс меняется на величину порядка импульса фотона , что и составит погрешность в определении импульса электрона . Следовательно, получим:

Это соотношение и носит название соотношение неопределенностей. Аналогичные соотношения имеют место и для других координат.

(4)

Таким образом, полученные соотношения связывают область локализации волнового пакета и область длин волн, для его реализации.