Взаимная индукция

Итак, в замкнутом контуре возникает ЭДС индукции , определяемая по закону:

Т.е. ЭДС индукции может возникать либо за счет изменения площади контура , либо за счет изменения индукции магнитного поля .

Поскольку магнитное поле может возбуждаться токами, текущими в каких либо проводниках, изменение индукции магнитного поля можно получить за счет изменения токов. Причем эти токи могут течь как в других контурах, так и в самом рассматриваемом контуре.

Если изменение индукции магнитного поля, соответственно и изменение магнитного потока, создается другим, по отношению к исследуемому, контуром, то говорят о взаимной индуктивности контуров, которую характеризуют коэффициентом взаимной индуктивности .

Если же изменение индукции магнитного поля создается током, текущим в самом исследуемом контуре, то говорят о самоиндукции контура, которую характеризуют коэффициентом самоиндукции .

В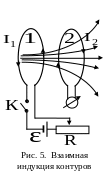 начале мы рассмотрим явление взаимоиндукции контуров, проводников.

Итак, имеются два, находящиеся недалеко друг от друга контура (см. рис. 5).

В цепь контура включен источник тока , который включается ключом . Сила тока в контуре изменяется с помощью реостата . При этом в контуре течет ток . Этот контур , по которому течет ток , создает вокруг себя магнитное поле с индукцией .

В месте нахождения -го контура, магнитный поток, создаваемый -м контуром равен . Поскольку индукция поля прямо пропорциональна току , текущему в первом контуре, то и магнитный поток будет прямо пропорционален току ‑ . Чтобы записать знак равенства, введем коэффициент пропорциональности, который обозначим как :

Здесь ‑ коэффициент взаимной индуктивности или взаимная индуктивность контуров и .

Взаимная индуктивность (коэффициент взаимной индуктивности) численно равен потоку магнитной индукции, создаваемому во втором контуре, если ток в первом контуре равен единице.

Размерность коэффициента взаимной индукции:

В СИ единица индуктивности имеет специальное наименование ‑ генри ‑ . Как мы выяснили ранее, размерность единицы индукции магнитного поля равна . Следовательно, размерность индуктивности будет иметь вид: . Это другой вид размерности индуктивности. Отсюда вытекает, что . При изучении закона Ампера, мы установили, что магнитная постоянная имеет размерность . Сравнивая два последних выражения, мы приходим к выводу, что размерность магнитной постоянной можно представить в виде: . Это более употребительная форма размерности магнитной постоянной, так как в таком виде она симметрична размерности электрической постоянной .

Далее, возвращаясь к взаимодействующим посредством магнитного поля контурам, можно рассуждать и наоборот. Во втором контуре имеется источник тока, второй контур создает магнитное поле и т.д. В результате мы придем к аналогичной формуле:

Из соображений симметрии ясно, но это можно и показать, что для одних и тех же двух контуров коэффициенты взаимной индуктивности и равны друг другу. Т.е. в действительности есть лишь взаимная индуктивность контуров:

И для магнитного потока, создаваемого током , можно записать общее выражение:

(2)

Т.о., во втором контуре возникает ЭДС индукции, равная:

Если контуры неподвижны друг относительно друга и если не меняется их конфигурация, то:

Здесь необходимо отметить еще следующее обстоятельство. Очевидно, что коэффициент взаимной индуктивности зависит от магнитных свойств среды, вмещающей контура. А магнитные свойства среды в общем случае зависят от магнитного поля, существующего в среде (например, ферромагнетики). Т.е., в конечном счете, от тока , т.е. от времени. Следовательно, в этом случае (ферромагнетики) , даже, если площадь контуров постоянна.

Исходя из последней формулы, можно дать другое определение коэффициенту взаимной индуктивности.

Коэффициент взаимной индуктивности двух контуров численно равен ЭДС индукции, возникающей в одном из контуров, при изменении силы тока в другом на единицу за единицу времени.

Для многосвязанных контуров магнитный поток увеличивается в раз, где ‑ число витков многосвязанных контуров. При этом вместо потока рассматривают величину ‑ потокосцепление, равную:

Коэффициент взаимной индукции двух контуров

Н айдем коэффициент взаимной индукции двух катушек, намотанных на общий тороидальный сердечник.

Мы уже показывали, что индукция магнитного поля тороида (6), приближенно может быть определена по формуле для магнитного поля соленоида :

Здесь ‑ ток, текущий через первую катушку, ‑ число витков на единицу длины первой катушки. Если магнитная проницаемость сердечника (об этой физической величине мы поговорим более подробно несколько позже), то индукция магнитного поля в сердечнике будет равна:

Здесь ‑ число витков первой катушки, ‑ длина тороида по средней линии. В этом случае, магнитный поток в сердечнике будет равен:

где ‑ площадь поперечного сечения сердечника тороида.

Поток магнитосцепления , пронизывающий вторую катушку, будет равен:

В этом случае, по определению:

(3)