2.8. Нелінійна парна регресія

Якщо між економічними показниками існують нелінійні співвідношення, то вони виражаються за допомогою відповідних нелінійних функцій. Серед нелінійних регресій розрізняють два класи: регресії, нелінійні за пояснюючою змінною, але лінійні за оцінюваними параметрами, і регресії, нелінійні за оцінюваними параметрами.

Прикладам регресій нелінійних за пояснюючою змінною можуть служити наступні залежності:

• поліноміальна:

, (2.8.1)

; (2.8.2)

• гіперболічна

. (2.8.3)

До регресій, нелінійних за оцінюваними параметрами, відносяться залежності:

• степенева

(2.8.4)

• показникова

(2.8.5)

• експоненційна

(2.8.6)

і т.д.

Регресії, нелінійні за пояснюючою змінною, легко зводяться до лінійних заміною змінних. Так, наприклад, (2.8.1) –(2.8.3) можна записати у вигляді:

; (2.8.7)

; (2.8.8)

, (2.8.9)

де зроблено заміни: , , і . Таким чином, у результаті лінеаризації одержимо: лінійне двофакторне рівняння (2.8.7), лінійне трифакторне (2.8.8) і лінійне однофакторне рівняння (2.8.9).

Параметри рівнянь (2.8.7) – (2.8.9) визначаються методом найменших квадратів. Застосування 1МНК для оцінки параболи другого ступеня (2.8.7) приводить до наступної системи нормальних рівнянь:

→ (2.8.10)

Розв’язавши цю систему рівнянь за формулами Крамера, одержимо

; ; , (2.8.11)

де визначники визначаються так

; ;

; .

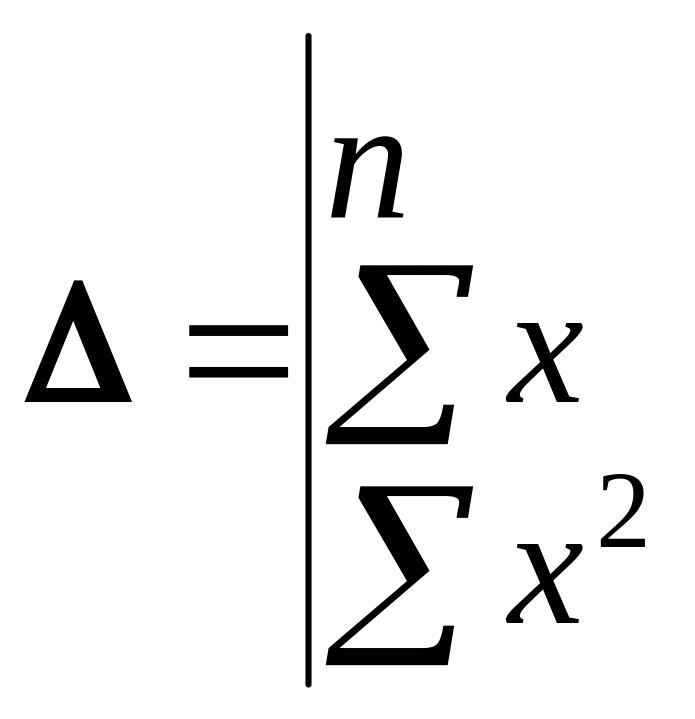
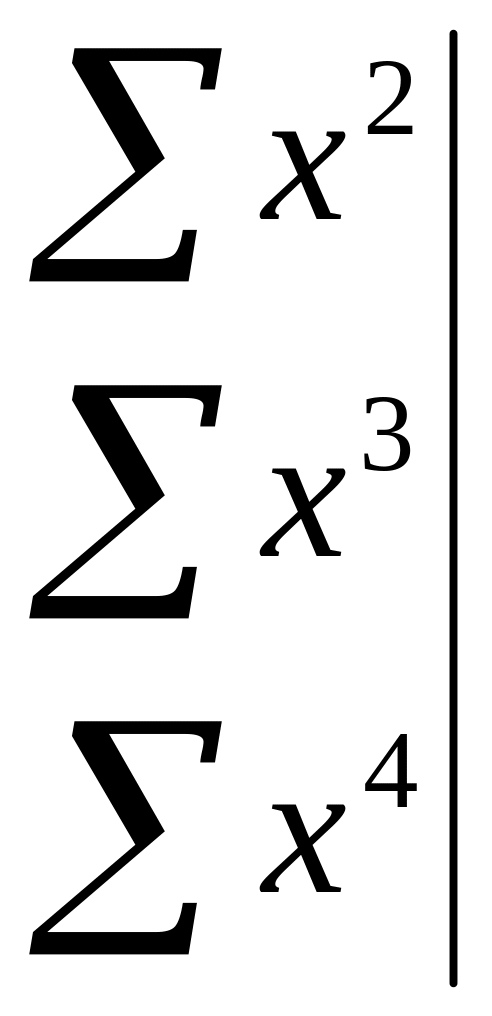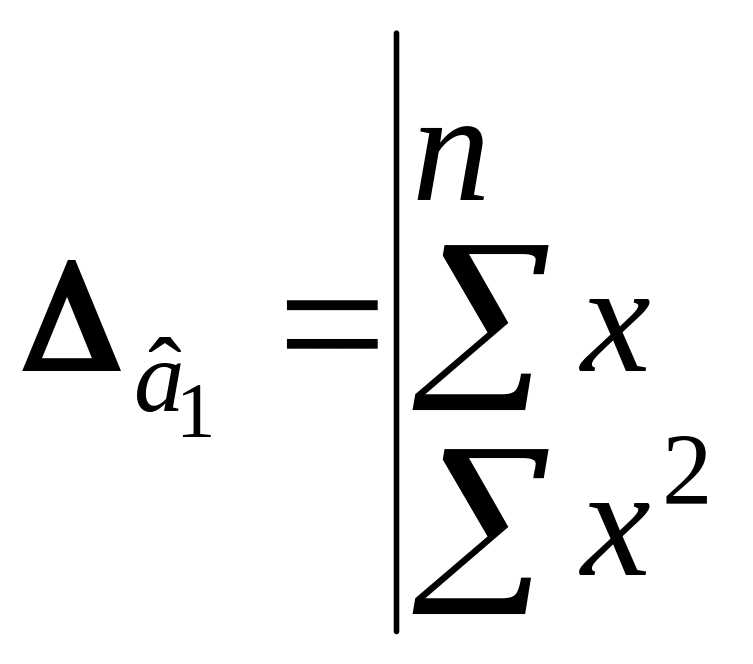
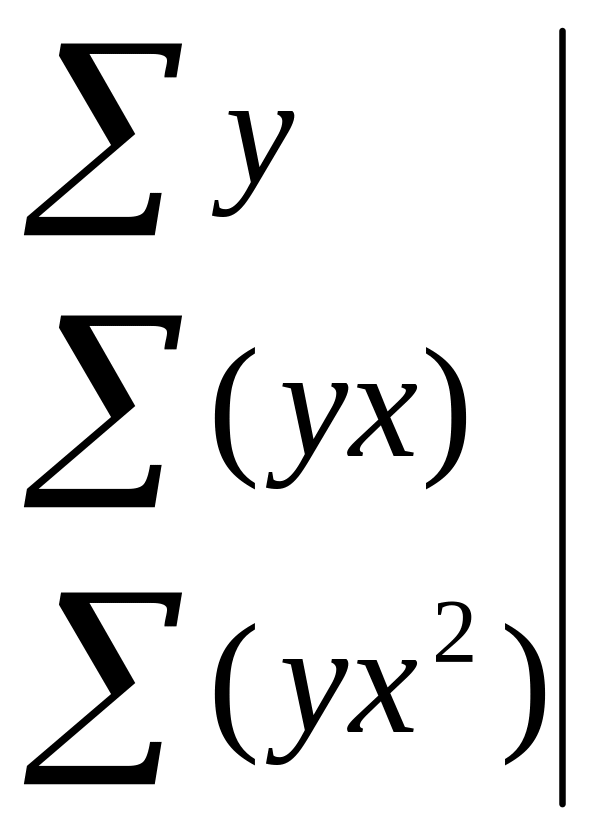Зауваження.

Більшість дослідників серед поліномів найчастіше використовують параболу другого ступеня. Обмеження у використанні поліномів високих ступенів пов'язані з вимогою однорідності досліджуваної генеральної сукупності: чим вище порядок полінома, тим більше вигинів має крива й відповідно менш однорідна сукупність за результативною ознакою. Крім того слід мати на увазі, що обсяг вибірки повинен у 6-7 разів перевищувати кількість параметрів моделі.

Аналогічно, для гіперболічної залежності (2.8.3) одержимо систему рівнянь:

→ (2.8.12)

Звідки параметри і :

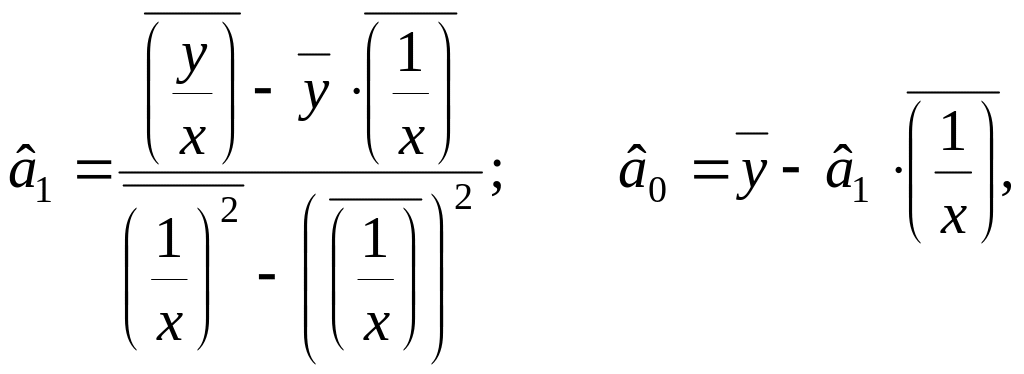(2.8.13)

де

; ; ;

.

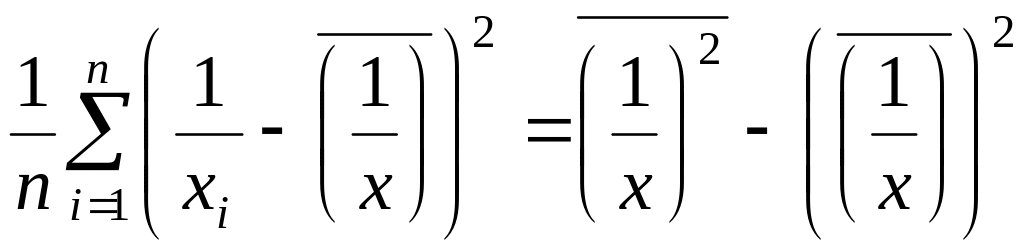Регресії нелінійні за оцінюваними параметрами також можуть бути перетворені до лінійного виду. Прологарифмуємо ліві і праві частини (2.7.4) – (2.7.6), та одержимо лінеаризовані рівняння:

або , (2.8.14)

або , (2.8.15)

або , (2.8.16)

де , , , .

Параметри рівнянь (2.8.14) – (2.8.16) також можна одержати методом найменших квадратів. Так для степеневої моделі одержимо систему нормальних рівнянь:

→ (2.8.17)

Звідки

(2.8.18)

і

, або , (2.8.19)

де , .

Параметр визначаємо потенціюванням , після цього підставляємо параметри і у рівняння регресії (2.8.4) і визначаємо степеневу функцію моделі.

Степеневу функцію застосовують, у теорії попиту та пропозицій. Це виробничі функції, криві освоєння для характеристики зв'язку між трудомісткістю продукції і масштабами виробництва в період освоєння випуску нового виду виробів і залежність валового національного доходу від рівня зайнятості.

Аналогічні перетворення можна виконати для показникової функції й одержати параметри і :

або (2.8.20)

і

або . (2.8.21)

Параметри і знайдемо потенціюванням:

, ,

підставляємо їх у (2.8.5) і знаходимо показникову функцію.

Для експоненційної функції параметри і в (2.8.6) мають вигляд:

і . (2.8.22)

Практичне застосування показникової функції і експоненти можливо, якщо результативна ознака не має від’ємних значень. Тому, якщо досліджується, наприклад, фінансовий результат діяльності підприємств, то дана функція не може бути використана.