
- •1. Основні теоретичні положення регресійного аналізу
- •1.1. Кореляційна залежність
- •1.2. Основні математичні поняття,
- •1.3. Передумови використання
- •2. Парний регресійний аналіз
- •2.1. Лінійна парна регресія
- •2.2. Властивості оцінок
- •2.3. Лінійний коефіцієнт кореляції
- •2.4. Коефіцієнт детермінації
- •2.5. Оцінка значущості рівняння регресії
- •2.6. Прогноз залежної змінної.
- •2.7. Приклад 1.
- •2.8. Нелінійна парна регресія
- •2.9. Дослідження нелінійних рівнянь
- •2.10. Приклад 2.
- •2.11. Побудова функції парної регресії
- •2.12. Побудова графіку функції
- •2.13. Питання для самоперевірки
- •3. Багатофакторний регресійний аналіз
- •3.1. Класична нормальна лінійна модель
- •3.2. Коефіцієнти детермінації і кореляції.
- •3.3. Перевірка значущості параметрів
- •3.4. Прогноз залежної змінної
- •3.5. Приклад 3. Знаходження двофакторної моделі
- •3.6. Використання пакету анализ данных
- •3.7. Використання Excel для розрахунку
- •Введення і підготовка даних
- •4. Мультиколінеарність
- •4.1. Поняття і наслідки мультиколінеарності
- •4.2. Алгоритм Фаррара – Глобера
- •4.3. Приклад 4.
- •4.5. Питання для самоперевірки
- •5. Гетероскедастичність
- •5.1. Поняття гетероскедастичності
- •5.2. Виявлення гетероскедастичності.
- •5.3. Приклад 5. Дослідження даних
- •5.4. Виявлення гетероскедастичності.
- •5.5. Приклад 6. Дослідження даних
- •5.6. Непараметричний тест Гольдфельда-Квандта
- •5.7. Питання для самоперевірки
- •6. Автокореляція
- •6.1. Поняття автокореляції.
- •6.2. Критерій Дарбіна-Уотсона
- •6.3. Приклад 7. Дослідження моделі на наявність
- •6.4. Питання для самоперевірки
- •7. Індивідуальні комплексні завдання
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Предметний покажчик
- •Література
- •Коефіцієнтів автокореляції залишків
- •Критичні значення і для коефіцієнта автокореляції залишків критерія Дарбіна-Уотсона для
- •Критичні значення і для коефіцієнта автокореляції залишків критерія Дарбіна-Уотсона для
- •Значення критерія Пірсона
- •Квантилі розподілу Стьюдента
- •83050, М. Донецьк, вул. Щорса, 31.
- •83023, М. Донецьк, вул. Харитонова, 10
Міністерство освіти і науки України
Донецький національний університет
економіки і торгівлі
імені Михайла Туган-Барановського
Кафедра вищої і прикладної математики
В.В. Фортуна, С.М.Латинін
ЕКОНОМЕТРИЧНІ МОДЕЛІ
Навчальний посібник
для організації самостійної роботи студентів
денної форми навчання
економічних спеціальностей
(в рамках кредитно-модульної системи навчання)
Затверджено на засіданні
кафедри вищої і
прикладної математики
Протокол № 24 від “ 18 ” 03 2009р.
Схвалено навчально-методичною
радою ДонНУЕТ
Протокол № від “ ” 200 9р.
Донецьк 2009
ББК 65в631я73
Ф 80
УДК 330.43(075.8)
Рецензенти:
д. фіз.-мат. наук, проф. Н.М. Лавріненко
д. фіз.-мат. наук, доцент О.К. Щетініна
Фортуна, В.В.
Ф 80 Економетричні моделі [Текст]: навч. посіб. для організації самост. роботи студ. ден. форми навчання екон. спец. (в рамках кредит.-модул. системи навч.)/М-во освіти і науки України, Донец. нац. ун-т економіки і торгівлі ім. М. Туган-Барановського, Каф. вищ. і приклад. математики; В.В. Фортуна, С.М.Латинін. – Донецьк:[ДонНУЕТ], 2009. – 126 с.
В умовах навчання за кредитно-модульною системою організації навчального процесу збільшується кількість годин виділених на самостійну роботу студентів за рахунок зменшення кількості аудиторних годин. В цих умовах ряд розділів курсу економіко-математичного моделювання студенти повинні будуть вивчати самостійно під керівництвом викладача.
Мета посібника – надати допомогу студенту при вивченні курсу економіко-математичного моделювання. При вивченні матеріалу значну увагу приділено виявленню змісту основних понять. Теоретичний матеріал ілюструється великою кількістю прикладів з розв'язками. Для контролю самостійної роботи в кінці розділів приводяться контрольні питання.
В кінці посібника наводяться 30 варіантів комплексних індивідуальних завдань.
Навчальний посібник призначений для студентів денної форми навчання економічних спеціальностей. Він може бути використаний студентами денної форми навчання інших спеціальностей, а також студентами заочної форми навчання.
ББК 65в631я73
© Фортуна В.В., Латинін С.М., 2009
© Донецький національний університет
економіки і торгівлі імені Михайла
Туган-Барановського, 2009
Зміст
|
|
|
стор. |
|||
|
Вступ………………………………............…………………………………..5 |
|
||||
1. |
Основні теоретичні положення регресійного аналізу……………6. |
|
||||
|
1.1. |
Кореляційна залежність…………………………………………..6. |
|
|||
|
1.2. |
Основні математичні поняття, які використовуються в регресійному аналізі………...……………………………........8 |
|
|||
|
1.3. |
Передумови використання методу найменших квадратів..11 |
|
|||
|
|
|
|
|||
2. |
Парний регресійний аналіз………………………………………........12 |
|
||||
|
2.1. |
Лінійна парна регресія. Метод найменших квадратів..……12 |
|
|||
|
2.2. |
Властивості оцінок………………………………………………..14 |
|
|||
|
2.3. |
Лінійний коефіцієнт кореляції….……………………………..15 |
|
|||
|
2.4. |
Коефіцієнт детермінації…………………………………………17 |
|
|||
|
2.5. |
Оцінка значущості рівняння регресії…………………………19 |
|
|||
|
2.6. |
Прогноз залежної змінної. Інтервальна оцінка функції регресії та її параметрів……………………………………….........23 |
|
|||
|
2.7. |
Приклад 1. Знаходження рівняння парної регресії…..........26 |
|
|||
|
2.8. |
Нелінійна парна регресія………………………………………..29 |
|
|||
|
2.9. |
Дослідження нелінійних рівнянь парної регресії ...…...…...32 |
|
|||
|
2.10. |
Приклад 2. Знаходження нелінійного рівняння парної регресії……………………….....……………………….....34 |
|
|||
|
2.11. |
Побудова парної регресії за допомогою Excel………….........39 |
|
|||
|
2.12. |
Побудова графіку функції регресії за допомогою Excel......42 |
|
|||
|
2.13. |
Питання для самоперевірки…………………………………….48 |
|
|||
|
|
|
|
|||
3. |
Багатофакторний регресійний аналіз ………………………………52 |
|
||||
|
3.1. |
Класична нормальна лінійна модель багатофакторної регресії …..........................................................52 |
|
|||
|
3.2. |
Коефіцієнти детермінації і кореляції. Оцінка значущості багатофакторної регресії ………………………………………….53 |
|
|||
|
3.3. |
Перевірка значущості параметрів рівняння регресії та коефіцієнта кореляції ……………………………………… ..56 |
|
|||
|
3.4. |
Прогноз залежної змінної………………………………………..57 |
|
|||
|
3.5. |
Приклад 3. Знаходження двофакторної моделі лінійної регресії…………………………………………..59 |
|
|||
|
3.6. |
Використання пакету АНАЛИЗ ДАННЫХ для багатофакторної регресії………………………………………...63 |
|
|||
|
3.7. |
Використання пакету Excel для розрахунку параметрів парної і багатофакторної регресії за формулами………………..67 |
|
|||
|
|
|
|
|||
4. |
Мультиколінеарність……..………………………………….………....78 |
|
||||
|
4.1. |
Поняття і наслідки мультиколінеарності ……………………78 |
|
|||
|
4.2. |
Алгоритм Фаррара-Глобера ……………………………………78 |
|
|||
|
4.3. |
Приклад 4. Перевірка на наявність мультиколінеарності за алгоритмом Фаррара-Глобера …………………………...... ….81 |
|
|||
|
4.4. |
Методи усунення мультиколінеарності………………………86 |
|
|||
|
4.5. |
Питання для самоперевірки ……………………………………87 |
|
|||
|
|
|
|
|||
5. |
Гетероскедастичність ……………………………………………………89 |
|
||||
|
5.1. |
Поняття гетероскедастичності і гомоскедастичності Наслідки гетероскедастичності…………………………..….....89 |
|
|||
|
5.2. |
Виявлення гетероскедастичності. Тест Гольдфельда-Квандта………………………………………91 |
|
|||
|
5.3. |
Приклад 5. Дослідження даних на наявність гетероскедастичності за тестом Гольдфельда-Квандта……………………………………………93 |
|
|||
|
5.4. |
Виявлення гетероскедастичності. Тест рангової кореляції Спірмена……………………………..95 |
|
|||
|
5.5. |
Приклад 6. Дослідження даних на наявність гетероскедастичності за тестом рангової кореляції Спірмена……………………………………97 |
|
|||
|
5.6. |
Непараметричний тест Гольдфельда-Квандта………………99 |
|
|||
|
5.7. |
Питання для самоперевірки ………………………………….100 |
|
|||
|
|
|
|
|||
6. |
Автокореляція ………………………………………..............................101 |
|
||||
|
6.1. |
Поняття автокореляції. Наслідки автокореляції..…..…......101 |
|
|||
|
6.2. |
Критерій Дарбіна-Уотсона………….………………………....102 |
|
|||
|
6.3. |
Приклад 7. Дослідження моделі на наявність автокореляції залишків…………………………………………104 |
|
|||
|
6.4. |
Питання для самоперевірки…………………………………..105 |
|
|||
|
|
|
|
|||
7. |
Комплексні індивідуальні завдання ……………………………....106 |
|
||||
|
|
|
||||
|
Предметний покажчик………………………………………………..115 |
|
||||
|
|
|
||||
|
Література……………………………………………………………… ..118 |
|
||||
|
|
|
||||
|
Додаток 1. |
Таблиця 5%-ого і 1%-ого рівнів ймовірності коефіцієнтів автокореляції…………………………... .119 |
|
|||
|
Додаток 2. |
Критичні значення
для коефіцієнта автокореляції залишків критерія
Дарбіна – Уотсона для
|
|
|||
|
Додаток 3. |
Значення критерія Пірсона
|
|
|||
|
Додаток 4. |
95% - квантилі розподілу
Фішера
|
|
|||
|
Додаток 5. |
Квантилі розподілу Стьюдента
|
|
|||
Вступ
Економетрія – це наука, що вивчає кількісні закономірності і взаємозалежності економічних процесів і об’єктів за допомогою математико-статистичних методів і моделей.
Можна виділити такі етапи економетричного дослідження:
специфікація економетричної моделі;
збір і підготовка економічної інформації;
оцінка параметрів економетричної моделі;
перевірка моделі на достовірність;
прогнозування на основі економетричної моделі.
Визначення. |
Економетрична модель – це рівняння (або система рівнянь), яка наближено представляє основні кількісні залежності між економічними змінними, що вивчаються. |
В найпростіших випадках
економетричні моделі є структурними,
тобто такими, що відображають сутність,
структуру, внутрішні взаємозв’язки
досліджуваного економічного об’єкта
чи явища. Така економетрична модель
кількісно описує взаємозв’язок між
вихідними показниками
![]() економічної системи та результативним
показником
економічної системи та результативним
показником
![]() .
У загальному випадку економетричну
модель можна записати
.
У загальному випадку економетричну
модель можна записати
![]() ,
,
де
![]() – випадкова або стохастична складова
економетричної моделі.
– випадкова або стохастична складова
економетричної моделі.
Показники бувають невипадковими і стохастичними (випадковими), але так як – випадкова величина, то і залежна змінна також випадкова незалежно від того якою є пояснювальна змінна . Отже, економетрична модель завжди є стохастичною.
Встановлення виду функції
![]() є задачею регресійного
аналізу.
є задачею регресійного
аналізу.
1. Основні теоретичні положення регресійного аналізу
1.1. Кореляційна залежність
Найпростішою задачею регресійного аналізу є парний регресійний аналіз, де вивчається залежність між двома змінними.
Залежність між двома змінними може бути:
функціональною, наприклад, залежність між почасовою заробітною платою і тривалістю робочого часу;
кореляційною, наприклад, залежність між урожайністю і кількістю добрив.
Кореляційною залежністю між двома змінними називається функціональна залежність між значеннями однієї з них і умовним математичним сподіванням (середнім значенням) іншої. Саме така залежність вивчається в економетрії. Ясно, що збільшення кількості добрив буде приводити до підвищення врожайності. Разом з тим, функціонального зв’язку між цими показниками немає, так як на врожайність впливають багато інших чинників. Однак цілком можливо, що між середнім значенням врожайності і кількістю внесених добрив буде функціональний зв'язок.
На практиці кореляційна залежність вивчається на основі вибіркових даних, в результаті чого отримують рівняння регресії:
![]() ,
,
де
![]() – умовна (групова) середня змінної
при фіксованому значенні змінної
– умовна (групова) середня змінної
при фіксованому значенні змінної
![]() ;
;
![]() – оцінки параметрів рівняння регресії,
– оцінки параметрів рівняння регресії,
![]() – функція регресії.
– функція регресії.
Метою побудови регресійної
моделі є вивчення відповідної генеральної
сукупності об’єктів чи процесів. Модель
будується на основі вибірки із
![]() спостережень. Вибірка формується
випадковим чином за певними правилами.
Тому на основі вибіркових даних можна
отримати тільки оцінки потрібних
параметрів, а не значення самих цих
параметрів. Оцінки значень факторної
ознаки
спостережень. Вибірка формується
випадковим чином за певними правилами.
Тому на основі вибіркових даних можна
отримати тільки оцінки потрібних
параметрів, а не значення самих цих
параметрів. Оцінки значень факторної
ознаки
![]() чи параметрів
чи параметрів
![]() позначаються
,
.
позначаються
,
.
Залежну змінну називають також функцією відгуку, пояснювальною, результативною, вихідною, ендогенною змінною, результативною ознакою, регресантом, а незалежну змінну – пояснюючою, вхідною, екзогенною змінною, фактором, факторною ознакою, регресором.
На практиці частіше всього можуть використовуватися такі види рівнянь парної регресії:
|
|
|
|
|
|
|
|
|
|
|
|
і інші.
При кожному і–ому
спостереженні (![]() )
величина
)
величина
![]() складається із двох доданків
складається із двох доданків
![]() ,
,
де
![]() – випадкова величина
(збурення).
Вона характеризує відхилення
реального (або спостережуваного) значення
результативної ознаки
– випадкова величина
(збурення).
Вона характеризує відхилення
реального (або спостережуваного) значення
результативної ознаки
![]() від теоретичного
від теоретичного
![]() (тобто розрахованого з рівняння регресії).
Числове значення випадкової величини
(тобто розрахованого з рівняння регресії).
Числове значення випадкової величини
![]() називають
залишком, похибкою.
називають
залишком, похибкою.
Присутність випадкової величини в моделі породжено, в основному, такими джерелами:
Специфікацією моделі. По-перше, регресійна модель є спрощенням реального економічного явища. Насправді, в загальному випадку крім включених в модель факторів
 ,
(
,
(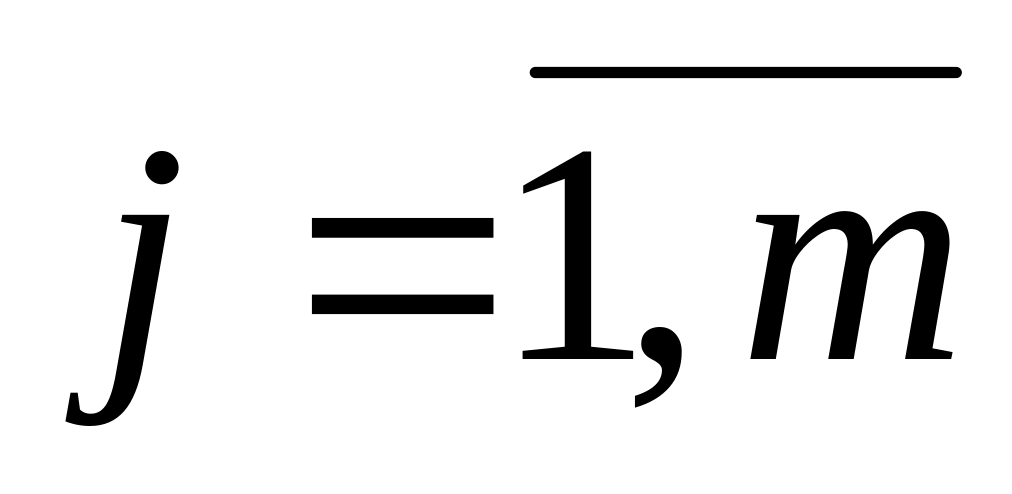 ),
є ще й інші фактори, які впливають на
пояснювальну змінну
,
але в модель не включені. По-друге,
вибрана функціональна специфікація
моделі також може не зовсім адекватно
відображати реальну залежність між
пояснювальною змінною
і пояснюючими змінними
.
),
є ще й інші фактори, які впливають на
пояснювальну змінну
,
але в модель не включені. По-друге,
вибрана функціональна специфікація
моделі також може не зовсім адекватно
відображати реальну залежність між
пояснювальною змінною
і пояснюючими змінними
.Неправильно визначеною структурою моделі. Наприклад, якщо вивчається залежність пояснювальної змінної від часу, тобто
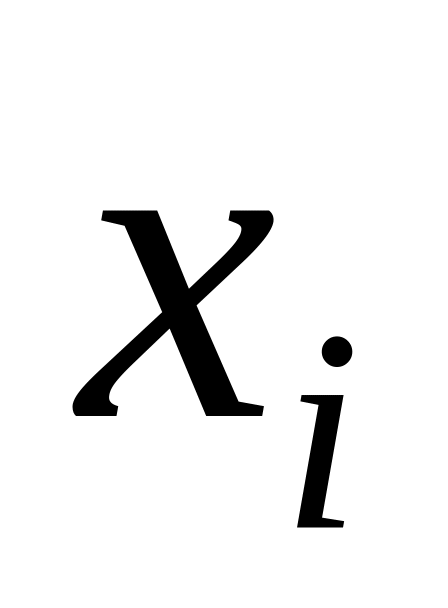 це певні моменти часу, то значення
може залежати не тільки від
,
але й від
це певні моменти часу, то значення
може залежати не тільки від
,
але й від
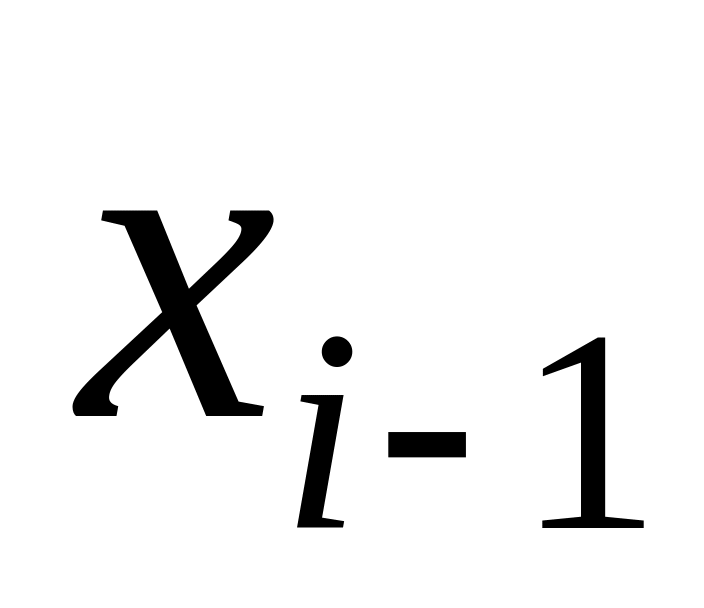 .
.Вибірковим характером вихідних даних, так як вибірки формуються випадковим чином.
Особливостями виміру змінних, можливими помилками при вимірюванні вихідних даних.
