2.6. Прогноз залежної змінної.

Інтервальна оцінка функції регресії і її параметрів

Рівняння регресії будується на основі вибіркових даних. Вибірка формується випадковим чином, тому і оцінки параметрів рівняння регресії є випадковими величинами. Отже, обчислені значення є насправді точковими оцінками істинних значень параметрів . Поряд з точковими оцінками параметрів рівняння регресії можуть бути обчислені й інтервальні оцінки. Інтервальні оцінки параметрів знаходяться за формулами:

,

, (2.6.1)

де – число ступенів свободи, , – стандартні похибки оцінок параметрів , які визначаються за формулами (2.5.7).

Одна з головних задач і один з важливих етапів регресійного аналізу це здійснення прогнозу. Якщо в модель (рівняння регресії) підставимо очікуване значення пояснювальної змінної , то отримаємо точковий прогноз значення пояснювальної змінної

. (2.6.2)

Щоб знайти інтервальну оцінку для умовного середнього значення (або ще кажуть довірчий інтервал для ) необхідно знайти середнє квадратичне відхилення для .

Зауваження.

Рівняння регресії дозволяє знайти оцінку умовного середнього значення регресанта, але для спрощення запису пишеться , замість .

Рівняння регресії може бути записане у вигляді (2.1.8)

.

В даному рівнянні і випадкові незалежні змінні. Нагадаємо, що відповідно до умов Гаусса - Маркова пояснююча змінна є не випадковою величиною, тому і множник не є випадкова величина. Тоді дисперсія буде мати дві складові

. (2.6.3)

Тут ми скористалися відомими властивостями дисперсії

,

де , – незалежні випадкові величини і .

Обчислимо

,

де дисперсія пояснювальної змінної , яка обчислюється за звичайними правилами і за фактичними даними. При отриманні останньої формули була використана четверта умова Гаусса – Маркова.

Для знаходження представимо оцінку даного параметра в явному вигляді

.

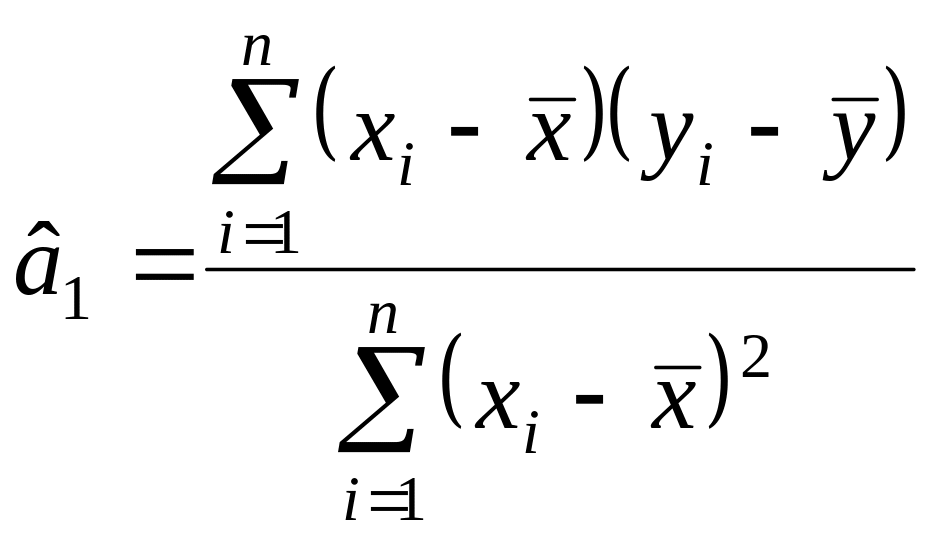Тоді знову враховуючи, що , і не є випадковими величинами отримаємо

.

В останньому виразі було враховано, що виконується четверта умова Гаусса –Маркова – , а також, що дисперсія відхилень дорівнює дисперсії самої змінної

Таким чином дисперсія знаходиться за формулою

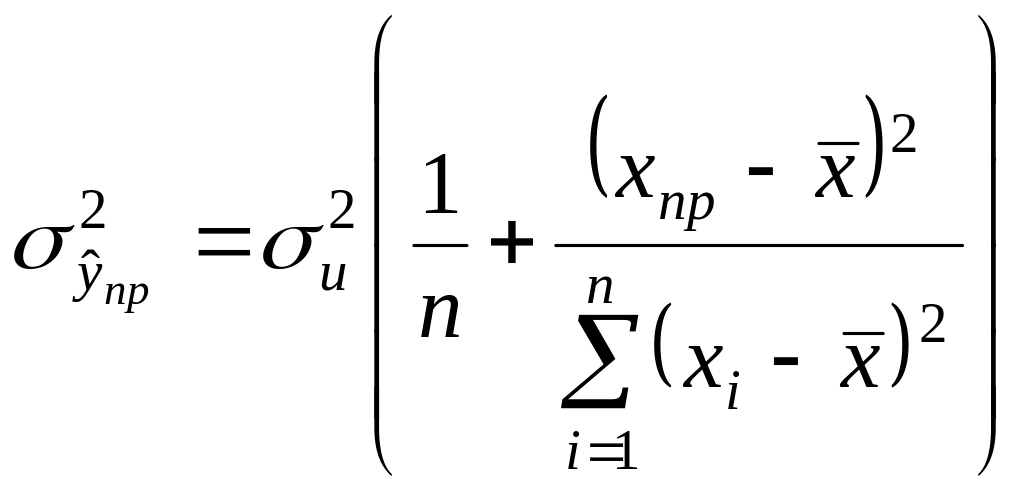, (2.6.4)

Так як нас цікавить незміщена оцінка , то 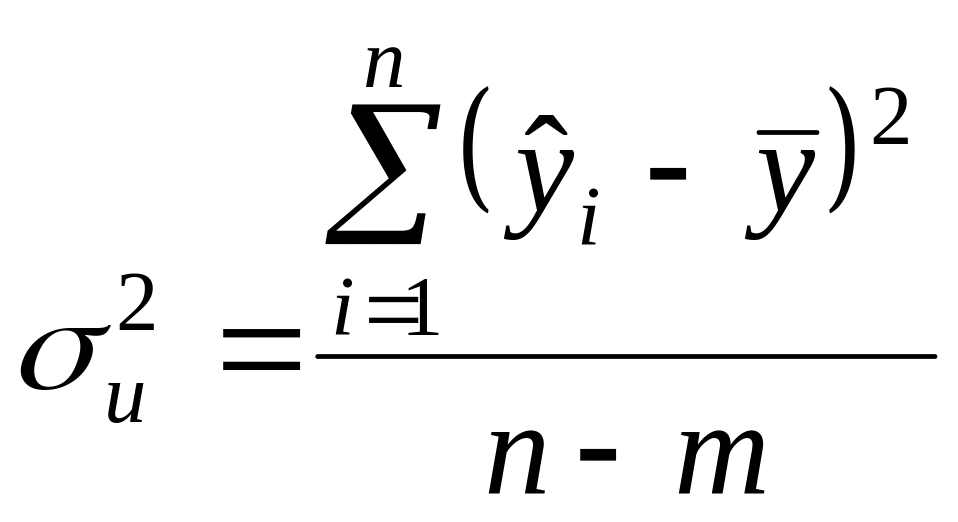- незміщена оцінка залишкової дисперсії, – обсяг вибірки, – число параметрів рівняння регресії.

Тоді довірчий інтервал для умовного математичного сподівання матиме вигляд

, (2.6.5)

де , .

Встановлений за формулою (2.6.5) інтервал означає, що з ймовірністю , середнє значення можливих значень регресанта буде знаходитися в межах .

Ясно, що чим ширший інтервал, тим менш цінним буде прогноз. З формул (2.6.4) і (2.6.5) видно, що:

• інтервал буде тим вужчим, чим меншою є залишкова дисперсія, тобто, чим точніше рівняння регресії апроксимує фактичні дані;

• найвужчим (найточнішим) буде прогнозний інтервал для 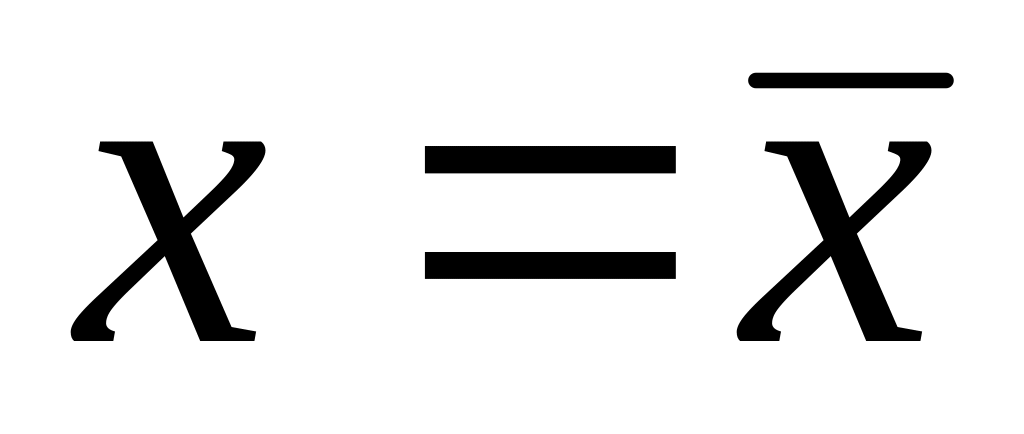, чим більше відхиляється від тим ширшим буде інтервал;

• інтервал можна звузити зменшивши надійність , так як при цьому зменшується .

Крім встановлення довірчого інтервалу для умовного середнього значення може бути обчисленим також довірчий інтервал для індивідуального значення. Ясно, що довірчий інтервал для індивідуальних значень буде значно ширшим ніж довірчий інтервал (2.5.5). При визначенні довірчих інтервалів для індивідуальних значень залежної змінної необхідно враховувати ще одне джерело варіації – розсіяння навколо лінії регресії, тобто в оцінку сумарної регресії включити ще й . Тоді дисперсія індивідуальних значень при дорівнює

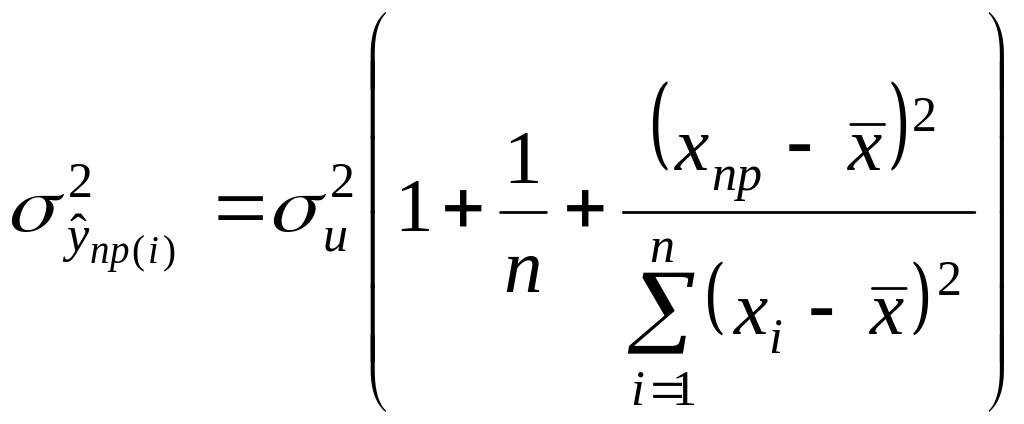. (2.6.6)

Відповідний довірчий інтервал для індивідуальних значень знаходиться за формулою

. (2.6.7)

В формулах (2.6.6) і (2.6.7) індекс означає “індивідуальне” значення.