1.3. Передумови використання

методу найменших квадратів

Для того, щоб отримати оцінки параметрів моделі ,…, які б були найкращими, тобто незміщеними, обґрунтованими і ефективними, необхідно щоб виконувалися ряд умов:

1. В моделі 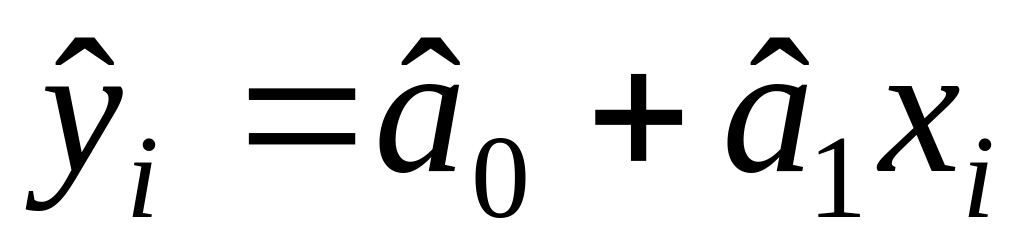(так само, як і в інших моделях) пояснююча змінна (пояснюючі змінні) є величиною детермінованою, а не випадковою.

2. Математичне сподівання збурення дорівнює нулю:

.

Або те саме, що математичне сподівання залежної змінної дорівнює функції регресії , тобто в лінійному випадку .

3. Дисперсія збурення (або залежної змінної ) постійна для довільного спостереження , .

.

4. Збурення і не корелюють

.

5. Збурення є нормально розподіленою випадковою величиною.

Якщо такі умови виконуються, то модель називається класичною нормальною лінійною регресійною моделлю (Classical Normal Linear Regression Model). Умови 1 – 5 називаються умовами Гаусса – Маркова.

При виконанні цих умов за допомогою методу найменших квадратів (ІМНК) можна отримати оцінки , які мають найменшу дисперсію в класі всіх незміщених оцінок.

У викладеному далі матеріалі вважається, якщо не зазначено інше, що всі ці умови виконуються.

2. Парний регресійний аналіз

2.1. Лінійна парна регресія

Найбільш простим і одночасно таким, що найчастіше зустрічається є парний лінійний зв’язок між ознаками.

Нехай маємо вибіркові дані про сукупні доходи населення в містах (ум.од.) і роздрібний товарооборот (ум.од).

Таблиця 2.1

Доходи населення, (ум.од.)	10	12	14	15	16	18	20
Роздрібний товарооборот, (ум.од)	8	11	13	14	15	15	18

Представимо вибіркові дані точками на координатній площині. Отримане зображення статистичної залежності називається кореляційним полем (рис 2.1). З виду кореляційного поля можна зробити припущення, що залежність між і лінійна. Тобто, вид кореляційного поля дозволяє зробити попереднє припущення про вид рівняння регресії.

			18
			16
			14
			12
			10
			8
				0						10		12		14		16		18		20

Рис. 2.1. – Кореляційне поле

Найбільш простим видом парної регресії є лінійна: .

Оцінки параметрів знаходяться методом найменших квадратів (1МНК): тобто вибираються такими, щоб сума квадратів відхилень фактичних значень від теоретичних була мінімальною:

, (2.1.1)

де – обсяг вибірки.

Зауважимо, що для знаходження можливі і інші підходи, наприклад може застосовуватися метод найбільшої правдоподібності.

Із (2.1.1.) на основі необхідної умови екстремуму функції двох змінних , прирівнюючи до нуля її перші частинні похідні, запишемо систему рівнянь



Звідки після елементарних перетворень отримуємо систему нормальних рівнянь для знаходження 1МНК оцінок параметрів

(2.1.2)

або, розділивши обидва рівняння на

(2.1.3)

де

, , , . (2.1.4)

Розв’язуючи (2.1.3) з врахуванням (2.1.4) отримаємо,

. (2.1.5)

. (2.1.6)

Для коефіцієнта справедливі також формули

В (2.1.5) , –дисперсія змінної , вибірковий кореляційний момент, або вибіркова коваріація.

Коефіцієнт називається вибірковим коефіцієнтом регресії (коефіцієнтом регресії) на . Він показує на скільки одиниць зміниться при зміні на одну одиницю.

Таким чином, обчисливши за формулами (2.1.5), (2.1.6) оцінки параметрів , отримаємо рівняння регресії

, (2.1.7)

або

. (2.1.8)

Як видно з останнього рівняння лінія регресії проходить через точку .