1.5 Отношения и функции

Пусть даны два множества А и В. Рассмотрим множество всевозможных пар вида (a, b), таких, что а  A, b  B. Мы получили новое множество, элементы которого имеют иную , чем элементы множеств А и В, природу. Например, таким образом, устроены обозначения клеток шахматной доски, декартовы координаты точек плоскости.

Определение 1. Множество А  В = {(а, b) | a  A, b  B} - всех упорядоченных пар элементов множеств А и В называется прямым или декартовым произведением множеств А и В.

Отметим, что в определении рассматриваются упорядоченные пары, т. е. (а, b)  (b, a), следовательно, А  В  В  А при А  В. В случае, когда А = В прямое произведение обозначается А  А = А² и называется декартовым квадратом множества А.

Этот способ построения множеств можно распространить на любое конечное число множеств.

Определение 2. Множество А₁  А₂  ...  А_n = {(а₁, а₂, ... , а_n) | а_i  А_i, i = =1, 2, ..., n} - всех упорядоченных n - ок вида (называется прямым произведением множеств А₁, А₂, ... , А_n.

Если А₁ = А₂ = ... = А_n = А, то пишут А₁  А₂  ...  А_n = Аⁿ и называют n - ой степенью множества А.

Определение 3. Отношением на упорядоченной системе множеств называется любое подмножество их прямого произведения, взятое в том же порядке.

Если R  А₁  А₂  ...  А_n , то по определению R - отношение на системе множеств А₁, А₂, ... , А_n. Для того чтобы зафиксировать число элементов в системе множеств, отношение R называют n - арным. В случае n = 2 , отношение называется бинарным; а при n = 1- унарным. Любое унарное отношение множества А является просто подмножеством множества А.

Примеры:

1. На множестве натуральных чисел N отношение R -“быть четным” является унарным отношением, множество R совпадает с подмножеством N₂ = = {2, 4, ... , 2n, ...} из N.

2. Если А и В - множество всех людей, то отношение “быть мужем и женой“ - это бинарное отношение на А, В.

3. Если А - множество всех женщин, В - множество всех мужчин, а С - множество всех детей, то “быть семьей из трех человек“ - это тернарное отношение ((а, b, c), где а - жена, b - муж, с - ребенок).

Рассмотрим подробнее бинарные отношения. Пусть А и В - некоторые множества, а R - бинарное отношение, т.е. R  А  В.

Областью определения бинарного отношения R называется множество D_R = {a  A |  b  B, (a, b)  R}, т.е. множество D_R составляют первые компоненты (координаты) всех пар, входящих в R.

Областью значений бинарного отношения R называется множество E_R = = {b  D |  a  A, (a, b)  R}, т.е. множество E_R составляют вторые компоненты (координаты) всех пар, входящих в R.

Любое бинарное отношение на A , B представляет собой множество пар, следовательно, для бинарных отношений обычным образом определены теоретико-множественные операции объединения, пересечения и т. д.

Определение4. Пусть R – бинарное отношение (R  АВ). Тогда обратным отношением для отношения R называется множество R ^-1 пар (b, a)  B A таких, что (a, b) R, т. е. R ^–1 = {(b, a) | b  B, a  A и (a, b)  R}. Отношение (R ^-1  B  A).

Определение 5. Пусть даны два бинарных отношения: R₁ на множествах А и В и R₂ на множествах В и С. Композицией (произведением) отношений R₁, R₂ называется множество R₂  R₁ пар (a, c) таких, что существует b B с условием (a, b)  R ₁, (b, c)  R₂, т.е.

R₂ R₁ = {(a, c) | a A, c  C и  b  B: (a, b)  R₁, (b, c)  R₂}.

Очевидно, что отношение R₁R₂ является бинарным отношением на множествах А и С.

Для любых бинарных отношений выполняются следующие свойства:

1. ( R ^-1) ^-1 = R.

2. (R₂R₁) ^-1 = R₁ ^-1  R₂^-1.

Доказательства этих свойств оставляем в качестве упражнений читателям.

Определение 6. Функцией из А в В называется бинарное отношение f   А  В, c условием, если из того, что (a, b)  f и (a, с)  f следует b = c.

Поскольку функции являются бинарными отношениями, то к ним применим интуитивный принцип объемности, т.е. две функции f и g равны (f = g), если они состоят из одних и тех же элементов. Область определения и область значения функции обозначается и определяется так же, как для бинарных отношений. Если область определения D_f функции f  А  В совпадает с А (D_f = А), то функцию f называют всюду определенной или говорят, что функция f задана на множестве А со значениями во множестве В.

Если f - функция из Х в Y, то вместо (x, y)  f привычно пишут у = f(x) и говорят, что у - значение, соответствующее аргументу х, или у - образ элемента х при отображении f. При этом х называют прообразом элемента у. Функцию f из X в Y (f  X  Y) называют одноместной или функцией одной переменной. Это понятие можно обобщить на случай функции нескольких переменных следующим образом. Функция f из Хⁿ в Y (f  Хⁿ  Y) называется n - местной функцией из Х в Y или функцией n - переменных и обозначается у = = f (x₁, x₂, ... , x _n).

Определение 7. Отображением множества А в множество В называется всюду определенная функция f  А  В. Если при этом область значений Е_f совпадает с В (Е _f = B), то f - отображение А на множество В. Иногда говорят, что отображение f устанавливает соответствие между множествами А и В. Отображение обозначают

f: А  В.

Пусть f - отображение множества М во множество N. Совокупность всех элементов из М, образом которых является данный элемент b  N, называется прообразом (или, точнее, полным прообразом) элемента b и обозначается f ^-1(b), т.е. f ^-1(b) = {m | m  M и f(m) = b}.

Если А  М, то образом множества А при отображении f называется множество f ( A) = {n | n = f (a) для всех а  А}, т.е. совокупность образов всех элементов множества А. В свою очередь для каждого подмножества В из N множество f ^-1(В) = {m | m = f ^-1(b) для всех b  В} называется прообразом множества В, т.е. f ^-1(В) - совокупность всех тех элементов из М, образы которых принадлежат В. Если ни один элемент b из В не имеет прообраза, полный прообраз f ^-1(В) = .

Сформулируем основные самые общие свойства отображений.

Теорема 1. Прообраз объединения двух множеств равен объединению их прообразов:

f ^-1(А  В) = f ^-1(А)  f ^-1(В).

Теорема 2. Прообраз пересечения двух множеств равен пересечению их прообразов:

f ^-1(А  В) = f ^-1(А)  f ^-1(В).

Теоремы 1 и 2 остаются в силе для объединений и пересечений любого (конечного или бесконечного) числа множеств.

Теорема 3. Образ объединения двух множеств равен объединению их образов:

f (А  В) = f (А)  f (В).

Утверждение аналогичное теореме 3 для пересечений не имеет места, т.е. в общем случае образ объединения двух множеств не совпадает с пересечением их образов. Например, если отображение f - это проектирование плоскости на ось ОХ, то множество А - отрезок: 0  х  1, у = 0 и множество В - отрезок: 0  х  1, у =1 не пересекаются (А В = ), а их образы совпадают (f(A) = f(B)).

Рассмотрим важный частный случай отображений - операции.

Определение 8. Отображение f из А в A называется операцией на множестве А.

В этом случае f(a)  A и операцию f называют унарной. На множестве действительных чисел R унарными операциями являются:

1. Операция нахождения обратного числа: f(x) = x^-1, x  0, или в других обозначениях: f = {(x, x^-1)| x  R, x  0};

2. Операция нахождения противоположного числа: f(x) = - x, или иначе: f = {(x, -x)| x  R};

3. Операция f = {(x, 0)| x  R} любое действительное число х отображает в 0.

Определение 9. Отображение из Аⁿ в А называется n - арной операцией на множестве А.

В случае n = 2 операция называется бинарной, а при n =3 - тернарной.

Операции сложения и умножения действительных чисел являются бинарными на множестве действительных чисел R . Например, операция сложения: f = {((x, y), x+y)| x, y  R}.

Определение 10. Алгебраической системой называется совокупность трех множеств: некоторого множества А , которое называют носителем, множества F - операций, заданных на А и множества предикатов - Р.

Алгебраические системы принято обозначать готическими буквами. Пусть  = А, F, P - алгебраическая система. Совокупность множеств {F, P} обозначается  и называется сигнатурой алгебраической системы .

Примеры:

1. Множество натуральных чисел N c определенными на нем бинарными операциями сложения (+), умножения () и нульместными операциями выделения нейтральных элементов нуля (0) и единицы (1), а так же с отношениями порядка () и равенства (=) является алгебраической системой:

 N; + ,  , 0, 1;  , = .

2. Множество действительных чисел с определенными на нем операциями сложения, умножения, вычитания (-), выделения нейтральных элементов, с отношениями порядка и равенства является алгебраической системой:

R , + , , - , 0, 1;  , = .

Заметим, что натуральный ряд как алгебраическая система не является подсистемой системы действительных чисел, поскольку они отличаются сигнатурами.

В математике важную роль играет специальное бинарное отношение - отношение эквивалентности. Это связано с проблемой разбиения тех или иных множеств на попарно непересекающиеся подмножества. Такие разбиения строятся на базе того или иного признака, которому элементы множества объединяются в классы. Например, множество всех треугольников можно разбить на классы равных между собой или на классы подобных треугольников. Признаки, на основе которых можно построить разбиение множества, должны обладать определенными свойствами. Поскольку признак можно моделировать бинарным отношением на множестве, то мы рассмотрим некоторые свойства бинарных отношений.

Определение 11. Пусть  - бинарное отношение на множестве А.

Отношение  называется рефлексивным на множестве А, если для любого элемента а  А пара (а, а)   ( или в других обозначениях: а ).

Отношение  называется симметричным на множестве А, если для любых элементов а, b  А из того, что (а, b)   следует, что (b, a)   (иначе: аb  ba).

Отношение  называется транзитивным на множестве А, если для любых элементов а, b, с  А из того, что (а, b)   и (b, c)   следует, что (a, c)   (иначе: аb и bc  ac).

Примеры:

1. Отношение включения () на множестве всех подмножеств некоторого множества А является бинарным отношением, причем оно рефлексивно (Х  Х), транзитивно (Х  Y и Y  Z  X  Z), но не симметрично (Х  Y   Y  X при X Y).

2. Отношение “меньше” () на множестве натуральных чисел обладает свойством транзитивности, но не является ни рефлексивным, ни симметричным.

Определение 12. Отношением эквивалентности на множестве А называется рефлексивное, симметричное и транзитивное на множестве А отношение.

Определение 13. Пусть  - отношение эквивалентности на множестве А. Классом эквивалентности, порожденным элементом а, называется подмножество множества А, состоящее из тех элементов b  А, для которых (а, b)   или ab.

Класс эквивалентности, порожденный элементом а, обозначается через [a] или С_а. По определению [a] = {b | b  A и ab}.

Примеры: 1. Отношение равенства на множестве целых чисел, очевидно, есть отношение эквивалентности. При этом каждый класс эквивалентности состоит из одного элемента, т.е. для любого целого числа х [x] = {x}.

2. Отношение подобия на множестве всех треугольников является отношением эквивалентности. Каждый класс эквивалентности представляет собой множество подобных между собой треугольников.

3. Покажем, что отношение сравнения по модулю натурального числа n на множестве целых чисел Z: х  y (mod n) тогда и только тогда, когда х - у делится на n, есть отношение эквивалентности. Это отношение рефлексивно на Z, так как для любого х  х - х = 0, и, следовательно, делится на n. Если х - у делится на n, то у - х делится на n, это означает симметричность отношения. Это отношение транзитивно, так как если х - у делится на n, то для некоторого целого r имеем х - у = rn, а если у - z делится на n, то для некоторого целого q имеем у - z = qn. Отсюда x - z = (r + q)n, т.е. x - z делится на n.

Данное отношение порождает следующие классы эквивалентности: вместе с любым целым числом а в этом же классе эквивалентности содержатся все числа вида а + kn, где k - целое число. Очевидно, что числа 0, 1, 2, ... , n - 1 порождают различные классы эквивалентности: [0], [1], [2], ... , [n - 1]. Они называются классами вычетов по модулю n . Поскольку любое целое число, а можно представить в виде а = qn + r, где 0  r  n, то все остальные классы эквивалентности совпадают с указанными выше.

4. Отношением эквивалентности на множестве всех учеников школы, очевидно, является отношение принадлежности одному классу. Классом эквивалентности в этом случае является множество учеников одного класса.

Для отношения эквивалентности  на множестве А справедливы следующие утверждения:

1. Если а  А, то а  [a] (т.е. каждый элемент А принадлежит порожденному им классу эквивалентности).

2. Если а, b  А и ab, то [а] = [b] (т.е. класс эквивалентности порождается любым своим элементом).

Справедливость первого утверждения следует из рефлексивности отношения : аа и, следовательно, а  [a] .Докажем второе утверждение. Пусть с  [b]. Тогда bc и в силу транзитивности отношения  ас, т.е. с  [a]. Отсюда [b]  [a]. Аналогично в силу симметричности  можно показать, что [а]  [b], а значит, [а] = [b].

Из приведенных выше утверждений следует, что любое отношение эквивалентности  на множестве А позволяет представить это множество в виде объединения попарно непересекающихся подмножеств – классов эквивалентности. Действительно, каждый элемент а из А лежит в порожденном им классе [a]. При этом любые два класса эквивалентности либо не пересекаются, либо совпадают, так как если с  [a] и c [b], то ас, откуда [a] = [c], и bс, откуда [b] = [c]. Следовательно, [a] = [b]. Такое представление множества А имеет специальное название.

Разбиением множества А называется совокупность попарно непересекающихся подмножеств А_k таких, что каждый элемент множества А принадлежит одному и только одному из этих подмножеств, т.е. А =  А_k, k   K и А _i  А _j =  при i  j.

Итак, нами установлено:

Всякое отношение эквивалентности определяет разбиение множества на классы эквивалентности относительно этого отношения.

С другой стороны справедливо утверждение:

Всякое разбиение множества А определяет на нем отношение эквивалентности : а b тогда и только тогда, когда a и b принадлежат одному подмножеству разбиения.

Действительно, рефлексивность и симметричность  очевидны. Докажем транзитивность. Пусть ab и bc, тогда a, b  A₁, b, c  A₂, где A₁ и A₂ - подмножества из разбиения множества А. Поскольку b  A₁, b  A₂, то A₁ = A₂. Следовательно, a, c  A₁ и aс.

Определение 14. Если  - отношение эквивалентности на множестве А, то совокупность всех классов эквивалентности называется фактор -множеством множества А по отношению эквивалентности  и обозначается А / .

Если а - элемент множества А, то порожденный им класс эквивалентности [a]  А/. Таким образом, элементами фактор-множества А/ являются не сами элементы множества А, а подмножества этого множества - классы эквивалентности (даже, если как в случае отношения равенства, каждый класс состоит из одного элемента).

Пусть на множестве А определено некоторое отношение эквивалентности  и бинарная операция, которая обозначена символом “+”, т.е. можно рассматривать алгебраическую систему: A, +. На фатор-множестве А /  индуцируем операцию “+” следующим образом: если a, b  А и a + b = c, то для соответствующих элементов [a] и [b] из А /  положим [a]  [b] = [a + b] = = [c], т.е. “суммой” двух классов эквивалентности назовем третий класс, порожденный элементом, который равен сумме представителей классов-слагаемых. Если построенное таким образом на А /  отношение является операцией, то А / ,   -алгебраическая система, которую принято называть фактор-системой. Однако фактор-множество не всегда превращается в фактор-систему. Рассмотрим несколько примеров.

Примеры:

1. Множество Z₀ - всех целых чисел без 0 с операцией умножения можно рассматривать как алгебраическую систему:  Z₀,  . Ясно, что множество всех положительных целых чисел и множество всех отрицательных целых чисел составляют разбиение множества Z₀, которое определяет отношение эквивалентности . Соответствующее ему фактор-множество Z₀/ = {a, b}, где а - множество целых положительных, а b - множество целых отрицательных чисел, можно превратить в фактор-систему {a ,b},  следующим образом: а  а = а, b  b = a, a  b = b  a = b. Действительно, произведение любых двух положительных чисел - число положительное, произведение любых двух отрицательных чисел - число положительное, а произведение двух чисел разных знаков - число отрицательное. Очевидно, что правило “умножения” на фактор-множестве не зависит от выбора представителя в классе эквивалентности и представляет собой правило умножения знаков.

2. Множество всех целых чисел - Z с операциями сложения и умножения представляет собой алгебраическую систему Z, +, . Классами эквивалентности, которые образуют фактор-множество, являются: класс положительных, класс отрицательных чисел и третий класс - ноль. Операция умножения и в этом случае индуцируется на фактор-множество, при этом правило умножения знаков (см. пример 1.) просто дополняется правилом умножения на 0. Однако операцию сложения на фактор-множестве задать нельзя, так как ее результат зависит от выбора представителя класса эквивалентности. Действительно, в силу равенств -1 + 1 = 0, -2 + 1 = -1 для соответствующих классов имеем: [-1]  [1] = [0] , [-2]  [1] = [-1], но [-1] = [-2], а [0]  [-1]. Итак, фактор-систему с операциями  и  получить нельзя.

Контрольные вопросы:

1. Определите декартово произведение двух множеств, декартов квадрат множества и прямое произведение. Приведите примеры.

2. Что такое отношение, какие виды отношений бывают? Примеры отношений.

3. Что вы понимаете под словами область определения и область значения?

4. Дайте определение множества R ^-1 пар (b, a)  B  A.

5. Что мы называем композицией отношений?

6. Перечислите свойства для бинарных отношений.

7. Какие определения функций вы знаете (перечислите их)? Приведите примеры функций.

8. Что означают слова – функция всюду определена?

9. Определите образ и прообраз элемента, и образ и прообраз множества. Примеры.

10. Что такое отображение, какие его свойства вы знаете?

11. Операция, унарная и n-арная операции.

12. Приведите примеры алгебраических систем, предварительно определив, что такое алгебраическая система.

13. Определите свойства бинарных отношений на множествах.

14. Отношение эквивалентности, класс эквивалентности. Приведите примеры. Разбиение на множестве, отношение эквивалентности. Примеры.

Контрольные задачи:

Понятие множества и элементы множества

1. Назовите три элемента множества:

а) учебных предметов, изучаемых в начальной школе;

б) четырех натуральных чисел;

в) четырехугольников.

2. Запишите, используя символы:

а) число 14 – натуральное;

б) число (-7) не является натуральным;

в) число 0 рациональное;

г) - число действительное.

3. Прочитайте следующие высказывания и укажите среди них верные:

   а) 100  N; б) – 8  Z; в) – 12  N;

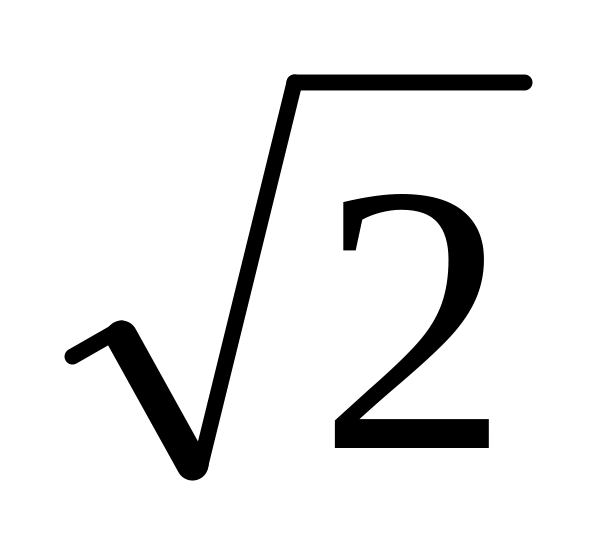
   г) 5, 36  Q; д) 102  R; е)  Q;

   ж) – 7,3  R; з) ¾  N; и) 0  N.

4. Р – множество натуральных чисел больших 7 и меньших 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат (используя знаки  и ).

5. Запишите множество букв в слове “математика” и множество цифр в записи числа 512535323.

Способы задания множеств

1. Запишите с помощью знака равенства и фигурных скобок предложения:

а) Х – множество чисел 0, 1, 2, 3, 4, 5;

б) Y – множество букв a, b, c.

2. Запишите, используя символы, множество Р, если оно состоит из натуральных чисел:

а) больших 100, но меньших 200;

б) меньших 150.

3. Перечислите элементы следующих множеств:

а) А – множество нечетных однозначных чисел;

б) В – множество натуральных чисел меньших или равных 20;

в) С – множество двухзначных чисел, делящихся на 10.

4. Укажите характеристическое свойство элементов множества:

а) {а, е, ё, и, у, о, э, ю, я, ы};

б) {78, 76, 74, 72, 70};

в) {111, 222, 333, 444, 555, 666, 777, 888, 999}.

5. Множество С состоит из квадрата, круга и треугольника. Принадлежат ли этому множества диагональ квадрата и центр круга?

Отношения между множествами

1. Даны два множества: X = {2, 4, 6} и Y = {0, 2, 4, 6, 8}. Верно ли что:

а) множества X и Y пересекаются;

б) множество X является подмножеством множества Y;

в) множества Р = {4, 0, 6, 8, 2} равно множеству Y?

2. Известно, что элемент а содержится в множестве А и в множестве В. Следует ли из этого, что:

а)   ;

б)   ;

в)   ?

3. Изобразите при помощи диаграмм Эйлера-Венна отношения между множествами С и D, если:

а) С – множество двузначных чисел,

D = {3, 43, 34, 56, 103};

б) С – множество двузначных чисел,

D – множество четырех натуральных чисел;

в) С – множество двузначных чисел,

D – множество трехзначных чисел;

г) С – множество двузначных чисел,

D – множество натуральных чисел, не меньше 10.

4. Дано множество Р = {3, 5, 7, 9}. Образуйте всевозможные его подмножества. Сколько их всего?

5. Какое из данных множеств является подмножеством другого:

а) А – множество натуральных чисел, кратных 2,

В – множество натуральных чисел, кратных 6,

С – множество натуральных чисел, кратных 3;

в) А – множество треугольников,

В – множество прямоугольных треугольников,

С – множество остроугольных треугольников.

Пересечение множеств

1. Сформулируйте те условия, при которых истины следующие утверждения:

   а) 5    ;

   б)     .

2. Известно, что х  . Следует ли из этого, что х    ?

3. Известно, что х    ;. Следует ли из этого, что х  ?

4. Найдите пресечения множеств А и В, если:

а) А = {a, b, c, d, e, f}, B = {b, e, f, k};

б) А = {26, 39, 5, 58, 17, 81}, B = {17, 26, 58};

в) А = {26, 39, 5, 58, 17, 81}, B = {17, 26, 58, 5, 39, 81}.

5. Из каких элементов состоит пересечение множества букв “математика” и множества букв в слове “геометрия”?

6. М – множество однозначных чисел, Р – множество нечетных натуральных чисел. Из каких чисел состоит их пересечение? Может ли оно быть пустым?

7. Начертите две фигуры, принадлежащие пересечению множеств С и D, если:

в) С – множество ромбов,

D – множество прямоугольников;

г) С – множество равнобедренных треугольников,

D – множество прямоугольных треугольников.

Объединение множеств

1. Сформулируйте те условия, при которых истины следующие утверждения:

   а) 6    ;

   б) 9    .

2. Известно, что х  . Следует ли из этого, что х    ?

3. Известно, что х    ;. Следует ли из этого, что х  ?

4. Найдите объединение множеств А и В, если:

а) А = {a, b, c, d, e, f}, B = {b, e, f, k};

б) А = {26, 39, 5, 58, 17, 81}, B = {17, 26, 58};

в) А = {26, 39, 5, 58, 17, 81}, B = {17, 26, 58, 5, 39, 81}.

5. Из каких элементов состоит объединение множества букв “математика” и множества букв в слове “геометрия”?

6. М – множество однозначных чисел, Р – множество нечетных натуральных чисел. Из каких чисел состоит их объединение? Может ли оно быть пустым?

7. Начертите две фигуры, принадлежащие пересечению множеств С и D, если:

в) С – множество ромбов,

D – множество прямоугольников;

г) С – множество равнобедренных треугольников,

D – множество прямоугольных треугольников.

Свойства пересечения и объединения множеств

1. Известно, что х    ;. Следует ли из этого, что:

а) х    ;

б) х    ;

в) х    .

2. Определите порядок действий в следующих выражениях:

а)     С; б)    С;

в)     С  D; г)     C  D.

3. Постройте три круга, представляющие попарно пересекающиеся множества , , С и отметьте штриховкой области, изображающие множества:

а)     С; б)     С;

в) (  )  С; г) (  )  C;

д)     С; е) (  С)  (  С).

Для каждого случая сделайте свой рисунок.

4. Проиллюстрируйте, используя диаграммы Эйлера-Венна, следующие свойства:

а) ассоциативности пересечения множеств;

б) дистрибутивности пресечения относительно объединения множеств;

в) дистрибутивности объединения относительно пресечения множеств.

5. Среди следующих выражений найдите такие, которые представляют собой равные множества:

   а)     С; б)   (  С);

   в)     С  D; г) (  )  C;

   д)   (  С); е) (  С)  (  С).

6. Даны множества:  - натуральных чисел, кратных 2;  - натуральных чисел, кратных 3; С – натуральных чисел, кратных 5.

а) Изобразите при помощи диаграммы Эйлера-Венна данные множества и отметьте штриховкой область, изображающую множество     С.

б) Сформулируйте характеристическое свойство элементов этого множества и назовите 3 элемента, которые ему принадлежат.

в) Верно ли, что     С = (  )  (  С)?

7. Докажите, что для любого множества  верны равенства:

а)    = ; б)    =;

в)    = ; г)    = .

8. Верно ли, что если   , то

а)    = ;

в)   В = В?

Вычитание множеств

1. Сформулируйте те условия, при которых истины следующие утверждения:

а) 7   \ ;

б) 4   \ .

2. Известно, что х   \ . Следует ли из этого, что:

а) х  ;

б) х  .

3. Найдите разность множеств  и , если:

а) А = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10};

б) А = {1, 2, 3, 4, 5, 6}, B = ;

в) А = {1, 2, 3, 4, 5, 6}, B = {1, 3, 5};

г) А = {1, 2, 3, 4, 5, 6}, B = {6, 2, 3,4, 5, 1}.

4. В каких случаях, выполняя упражнение 3, вы находите дополнение множества  до множества ?

5. Найдите дополнение множества Y до множества Х, если:

а) Х – множество точек прямой АВ, Y – множество точек отрезка АВ;

б) Х – множество точек квадрата, Y – множество точек круга, вписанного в этот квадрат;

в) Х – множество прямоугольников, Y – множество квадратов.

6. Из каких чисел состоит дополнение:

а) множество натуральных чисел до множества целых;

б) множество целых чисел до множества рациональных;

в) множество рациональных чисел до множества действительных.

7. Постройте три круга, изображающий три попарно пересекающихся множества А, В и С, и выделите каким-либо образом области, представляющие множества:

а)    \ С; б)  \   С;

в)  \ С   \ С; г)  \   C;

д)  \   С; е)  \   С.

8. Проверьте, верны ли равенства и проиллюстрируйте их при помощи диаграмм Эйлера-Венна:

а)  \ (  С) = ( \ )  ( \ С);

б)  \ (  С) = ( \ )  ( \ С);

в) (  ) \ С = ( \ )  ( \ С);

г) (  ) \ С = (  ) \ (  С).

9. А – множество натуральных чисел, кратных 7, В – множество натуральных чисел, кратных 3, А – множество четных натуральных чисел. Из каких чисел состоят множества:

а) (  ) \ С; б) ( \ )  С;

в)   С \ ; г) C   \ .