1. 2. Операции над множествами
Рассмотрим операции над множествами, которые представляют собой ряд правил, позволяющих получать новые множества из уже заданных.
Объединением (суммой) двух множеств А и В называется множество А В, все элементы которого являются элементами множества А или В:
А В = {x | x A или x В}.
Другими словами, в объединение А В входят все элементы как множества А, так и множества В, т. е. А А В и В А В.
Пример. Если А = {1, 2, 3}, B = {0, 1, 5}, то А В = {0, 1, 2, 3, 5}.
Для любой совокупности множеств под их объединением будем понимать новое множество, каждый элемент которого является элементом некоторого множества из данной совокупности, при этом, любой элемент каждого множества совокупности есть элемент объединения. В частности, для А1, А2, ..., Аn, ..., A = A i = {x | x A i, i = 1, 2, ..., n, ...}.
Пересечением множеств А и В называется множество А В, элементами которого являются элементы обоих множеств А и В:
А В = {x | x A и х В}.
Другими словами в пересечение А В входят только те элементы А, которые входят в В. Если ни один элемент множества А не является элементом множества В, то очевидно, что А В = . В этом случае говорят, что множества А и В не пересекаются. Ясно, что А В А и А В В.
Пример. Если А = {a, b, c, d}, B = {a, c, d, e, f}, то А В = {a, c, d}.
Для произвольной совокупности множеств под пересечением будем понимать новое множество, состоящее из тех и только тех элементов, которые входят во все множества данной совокупности. В частности, для А1, А2, ..., А n, ... , A = A i = {x | x A i, для всех i = 1, 2, ..., n, ...}.
Разностью множеств А и В называется множество А \ В, элементами которого являются только те элементы множества А, которые не принадлежат множеству В:
А \ В = {x | x A , но х В}.
Например, для множеств А и В, из предыдущего примера, А \ В = {b}.
Симметрической разностью множеств А и В называется множество А В = (А \ B) (B \ A). Другими словами, это множество состоит из тех и только тех элементов А и В, которые не входят в пересечение этих множеств.
Например, для множеств А и В, А = {a, b, c, d}, B = {a, c, d, e, f}, А В = = {b, e, f}.
Можно доказать, что А В = (А \ B) (B \ A) = (А B) \ (А В).
Дополнением
множества
А
называется множествоА
всех
тех элементов, которые не принадлежат
А.
Если предположить существование универсума U, то А = U \ A.
Разность Х \ А = {x | x X, x A}, т.е. множество всех элементов Х, которые не принадлежат А, иногда называют относительным дополнением множества А до множества Х. Отметим, что Х \ A = X А.
Для наглядного представления отношений между подмножествами какого-либо универсального множества используют диаграммы Эйлера - Венна. Само универсальное множество U изображают в виде прямоугольника, а его подмножества - в виде кругов, расположенных внутри прямоугольника.
Диаграммы Эйлера - Венна, иллюстрирующие операции над множествами:
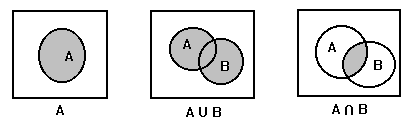
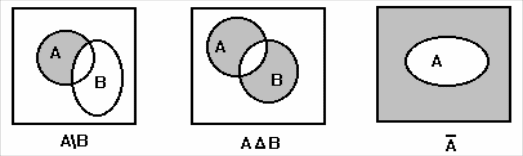
Рис. 1
Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества:
1. Коммутативность:
А В = В А ; А В = В А ;
2. Ассоциативность:
А (В С) = (А В) С; А (В С) = (А В) С;
3. Дистрибутивность:
А (В С) = (А В) (А С); А (В С) = (А В) (А С);
4. А = А, А U = U; А = , А U = А;
5. А А = U; А А = ;
6. Идемпотентность:
А А = А; А А = А;
7
.
Законы де
Моргана:
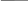А
В
= А
В;
А
В
= А
В;
8. Закон поглощения:
А (А В) = А; А (А В) = А.
Докажем тождество 3: А (В С) = (А В) (А С).
Обозначим М = А (В С) и N = (А В) (А С). Равенство M = N равносильно () двум включениям: М N , N M.
Сначала докажем, что М N. Пусть х М = А (В С). Это означает, что х А или х В С. Если х А, то х А В и х А С. Следовательно, х (А В) (А С) = N. Первое включение доказано.
Покажем, что N M. Пусть х N = (А В) (А С), тогда х А В и х А С. Следовательно, либо х А, и тогда очевидно, что х А (В С), либо х В и х С, т.е. х В С, а значит х А (В С)= М.
Остальные тождества доказываются аналогично.
Упражнение: Докажите оставшиеся аксиомы.
Контрольные вопросы:
Перечислите операции над множествами, которые вы знаете, и дайте их определение.
Запишите тождества, которые выполняются для этих операций.