2.4 Моделирование величин классами эквивалентности на множествах

Система величин как аксиоматическая теория, задает некоторую (математическую) рамку, и не задает подходов к методике математике в начальной школе, где дети должны иметь дело (действовать) конкретными вещами (объектами), имеющим конкретную длину, вес, площадь, объем. Поэтому возникает два вопроса.

Где те интерпретации (модели) данной аксиоматической теории, которые имеют дочисловую природу и могут быть положены в основания методики работы в начальной школе?

Где теоретические основание эмпирических понятий величины из программы 1-го класса РО?

В данном разделе мы и хотим изложить один из подходов в построении таких моделей с помощью теории множеств. Подтвердив еще раз тот факт, что в настоящее время в основании любых разделов математики в том числе и в методике математики начальной школы РО лежит теория множеств, а не эмпирическое понятие числа, как в традиционной методике.

В основе подхода лежит идея моделирования множествами признаков предметов. В основе лежит математическая способность человека в предметах видеть “одинаковое” и ”объединять” это в признаки. В онтогенезе (и следовательно в филогенезе) эти (математические) способности являются одними из первых.

Эта идея впервые была опробована нами (совместно с А.М. Ароновым) в экспериментальном курсе математики со студентами в КрасГУ в 1986 году. Возможность “помыслить” “красное” как множество всех красных объектов (предметов) и обратно – множество всех красных предметов помыслить как признак “красное”, позволяет гораздо быстрее строить совместные адекватные представления о множестве не только с помощью количественной (как совокупность), но и качественной характеристики (как абстрактная характеристическая функция (множество)). Такой подход полезен и при изучении операций на множествах, он позволяет ”связать” натуральное представление об объединении, пересечении, с логическими операциями на характеристических функциях.

Как это может быть применено к методике математики начальной школы РО? Начнем с примера. Пусть М – множество всех (мыслимых) предметов, обладающих свойством протяженности (имеющих длину). Мы можем довольно ясно представить себе все непосредственные и опосредованные способы сравнения этих предметов по длине, и конструирования (составления) из них других (“длинных”) предметов. На множестве М зададим отношение эквивалентности. Два предмета а и b будем считать эквивалентными, если они совпадают по протяженности (имеют одинаковую длину). Так введенное отношение действительно является отношением эквивалентности (это легко проверить). Класс, содержащий элемент а, обозначим так [а] и зададим отношение порядка, и операцию сложения на классах через представителей (на языке представителей):

[а]  [b] ^_ (а  b)

[а] + [b] = [а  b],

где “” - способ сравнения предметов а и b по длине, а значком  обозначен способ конструирования (сравнения) предмета (а  b) из предметов а и в. “Туман” рассеивается, если учесть, что во множество М полагают и все отрезки. Поэтому действия  и  можно понять как сравнение отрезков по длине и построение отрезка (а  b) составленного из отрезков а и b. Легко проверяется, что классы эквивалентности с введенными на них порядков и суммой удовлетворяют всем свойствам системы величин (см. предыдущий раздел). Эта система величин и называется системой длин. Аналогично можно построить системы объемов, площадей, масс. Теперь сделаем обобщение.

Пусть М – множество всех (мыслимых) предметов, обладающих некоторым количественным свойством ””, т.е. эти предметы как-то практически можно сравнивать по свойству ””. Как и в предыдущем примере мы можем задать отношение эквивалентности на множестве М и на классах эквивалентности построить (задать) отношение порядка и операции сложения на языке представителей:

[а]  [b] ^_ (а  b)

[а] + [b] = [а  b],

где “” - способ сравнения предметов а и b по свойству ””, а значком  обозначен способ “конструирования” предмета а  b из а и в.

Так введенное сложение позволяет “проверить” выполнение “величинных” аксиом. Тем самым определить (описать) условия на способы сравнения “” и конструирования . Кроме того, можно рассмотреть объект:

Так возникает представление о разах или натуральном параметре. Вполне нормальная процедура, связанная с обозначением оговоренных смыслов.

Контрольные задачи:

Логические связки. Таблицы истинности

1. Приведите примеры высказываний (истинных и ложных), которые можно записать одними только знаками, без слов.

2. Приведите примеры высказываний (истинных и ложных), которые одними только вам известными знаками записать невозможно.

3. Прочтите словами следующие высказывания, записанные знаками; какие из этих высказываний истины, а какие ложны?

5 < 2;

11 + 3 = 18;

2 + 4  10;

53 = 125;

63  216.

4. Сформулируйте отрицания следующих высказываний:

а) М  {257 – четное число};

б) Q  {число рационально};

в) R  {число 7 положительно};

г) S  {число 5 отрицательно}.

5. Для каждого из следующих высказываний составьте отрицание, а затем двойное отрицание. Убедитесь, что двойное отрицание по смыслу совпадает по смыслу с исходным высказыванием:

а)   {15 делится на 3};

б)   {5 – число положительное};

в) С  {3 < 7};

г) D  {5*7 = 35}.

6. Постройте отрицания высказываний и укажите в каждом случае, какое из высказываний – исходное или полученное, - истинно:

а)   {при каждом a > 0 уравнение х² = а имеет действительный корень};

б)   {при любом действительном a уравнение х² = а имеет действительный корень};

в) С  {существует квадратное уравнение, не имеющее действительных корней};

г) D  {хотя бы одно из произвольных двух чисел a, bделится на 3}.

7. Запишите с помощью знаков   следующие высказывания:

а) Не всякая простая дробь выражается конечной десятичной дробью.

б) Каково бы ни было натуральное число х, найдется такое натуральное число у, что х + у – простое число.

в) Каково бы ни было натуральное число х, можно подобрать такое натуральное число у, что х² + у² < 100.

г) Каково бы ни было натуральное число у, среди натуральных чисел найдется такое х, что х + у – четное число.

8. Запишите знаками следующие высказывания, составьте отрицания этих высказываний и прочтите их словами:

а) Любое натуральное число делится на 5.

б) Существуют четные простые числа.

в) Все натуральные числа четны.

г) Существует треугольник с двумя прямыми углами.

9. Выпишите все подформулы формулы .

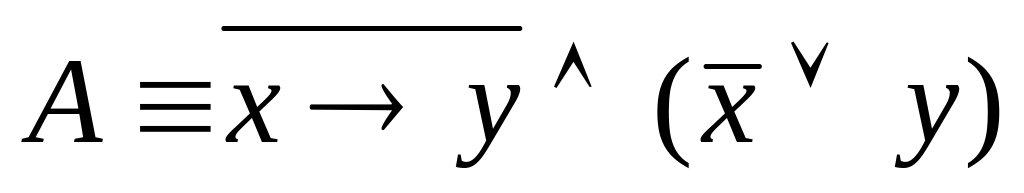10. Применяя правило подстановки, доказать, что доказуема формула:

а) ;

б) ;

в) ;

г) ;

д) .

11. Применяя произвольные правила вывода, показать, что доказуемы формулы:

а) ;

б) ;

в) ;

г) ;

д) .

12. Составьте таблицу истинности для высказывания .

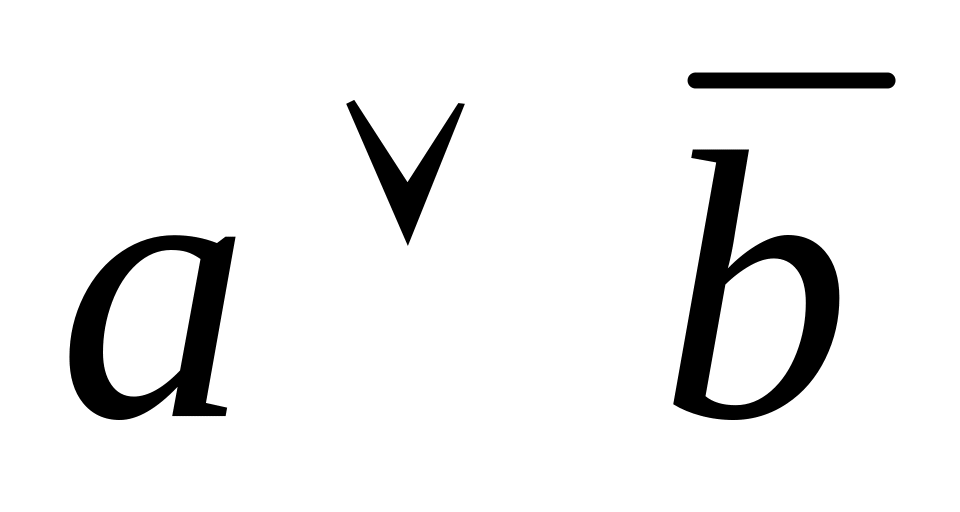13. Составьте таблицу истинности для формул:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) .

14. Проверьте, не составляя таблиц истинности, являются ли следующие формулы тождественно истинными:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

15. Доказать равносильность:

а) ;

б) ;

в) ;

г) ;

д) .

16. Упростите формулы:

а) ;

б) ;

в) .