Глава 5. Комплексные числа

5.1. ВЕКТОРЫ. СИСТЕМА НАПРАВЛЕННЫХ ВЕЛИЧИН

Представление о векторах как о направленных отрезках, которое дается в школе требует некоторого уточнения. Правильнее, на наш взгляд, было бы говорить о системе направленных величин, а направленные отрезки использовать как модели направленных величин. Это соответствует логике нашего курса, просматривается ход от графического изображения величин к направленным величинам. Моделировать направленные величины было бы точнее классами эквивалентностей на направленных отрезках. Где отношение эквивалентности задается равенством направлений и длин отрезков. Тогда каждый направленный отрезок может быть рассмотрен как представитель класса эквивалентных отрезков и, следовательно, является представителем изучаемой величины.

В этом месте возможно понимание направленных величин по аналогии с методической разработкой Д.А. Трапезникова, в которой рассматривается моделирование величин отрезками, а здесь направленные величины (скорость, время и т.д.) [20].

Остановимся на системе плоских направленных величин, которые могут быть изображены отрезками на плоскости. Для таких векторов легко ввести нулевой вектор, как класс всех отрезков имеющих нулевую длину. Такие направленные величины будем обозначать строчными латинскими буква с чертой над ними. Понятно, что на таких направленных отрезках можно ввести операции сложения, умножения на число и даже, так называемое, скалярное произведение. Подробно, если – вектор, – вектор, то ( ) – вектор, и этот вектор определяется по правилу параллелограмма: ( ) =

Если ά – действительное число, то ά - тоже вектор, его иногда называют вытянутым ά-раз относительно вектора . Если = 0, то 0 – вектор (нулевой вектор). Скалярное произведение , это есть число, которое записывается в виде:

Свойство векторов и операции над ними:

1. для любых векторов и справедливо следующее утверждение: + = + ;

2. для любых векторов , и имеет место: ( + ) + = + ( + + );

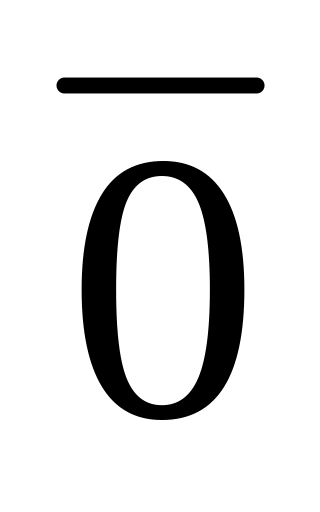3. + = , где - нулевой вектор;

4. для любого вектора существует вектор (- ) такой, что: + (- ) = = 0.

Упражнение: Докажите эти свойства.

Следующая группа свойств:

1. для любого вектора : 1* = ;

2. ( ) = () , где  и  - числа;

3. (  )   +  ;

4. для любых двух векторов и : ( + )   +  .

Можно доказать, что:

5) 0* = , где 0 – число.

Упражнение: Докажите эти свойства.

Группа свойств скалярного произведения:

1. для любых векторов и выполняется следующее свойство: ( , ) = ( , ), где  является скаляром;

2. для любых трех векторов , и имеет место следующее свойство: ( + , ) = = ( + ), т.е. свойство ассоциативности;

3. ( , ) = ( , ) - свойство коммутативности;

4. для любого вектора справедливо следующее свойство ( , )  0, при этом, если вектор является не нулевым вектором (т.е.  ), то ( , ) < 0.

Упражнение: Докажите эти свойства.

Контрольные вопросы:

1. Что мы понимаем под направленными величинами? Постройте модель направленных величин. Приведите примеры направленных величин.

2. Задайте нулевой вектор. Соотнесите его с системой направленных величин.

3. Задайте операции над направленными отрезках (сложение, умножение на число и скалярное произведение). Приведите примеры на каждую операцию.

4. Расскажите (или нарисуйте) правило параллелограмма. Пример.

5. Сформулируйте свойства векторов и операции сложения. Примеры.

6. Сформулируйте свойства для операции умножения. Примеры.

7. Сформулируйте свойства скалярного произведения. Примеры.

2. КОМПЛЕКСНЫЕ ЧИСЛА КАК ОТНОШЕНИЯ ВЕКТОРОВ

Ранее комплексные числа изучались в средней школе. Потом на каких-то основаниях их изъяли из школьного курса математики. Но на самом деле представление о мнимых (ничего не моделирующих), получаемых из преобразования модели чисел, имело, на наш взгляд, большое значение: то, что В.В. Давыдов называет работой с чистыми моделями, и задавало высокий уровень знаний старшеклассников. Мы включаем этот раздел математики в наш курс, т.к. это соответствует логике нашего курса.

Зададим числовую ось. Мы знаем, что каждая точка этой оси моделирует действительное число (а сама ось – непрерывное линейное поле действительных чисел). Расширим эту числовую модель до плоскости, т.е. введем еще одну координатную прямую, ортогональную оси Х, и обозначим оси этой плоскости ОХ и ОY соответственно. Теперь каждая точка плоскости получила координаты. Постараемся теперь превратить (понять) как можно построить числа с помощью этой модели¹.

Для того чтобы точку превратить в число необходимо понять правила сложения и умножения. Будем действовать через координаты.

Пусть и - точки плоскости с соответствующими координатами, тогда точка является суммой точек и определяются следующим образом: х₃ = (х₁ + х₂), у₃ = y₁ + у₂.

Точка  = (х₄, у₄) является произведением точек  и , определяемых следующим образом:  = (х₁х₂ - у₁у₂, х₁ у₂ + х₂ у₁).

В качестве нуля (0) этой плоскости выбирается точка 0 = (0,0) – координаты точки, в качестве единицы 1 – точка 1 = (1, 0). Эти точки моделируют на оси вещественный ноль и вещественную единицу.

Так получаемое числовое множество с операциями сложения и умножения называются полем комплексных чисел.

А все точки, вторая координата которых равна 0, фактически моделируют вещественные числа. Таким образом, поле вещественных чисел включается в поле комплексных чисел.