Добавил:

sutkowska92 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бухарский инженерно-технологический институт

Предмет:

Высшая математика

Файл:

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf

Скачиваний:

177

Добавлен:

27.05.2019

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 208 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Глава V ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

§ 1. Задача о площади криволинейной трапеции

Рассмотрим функцию f (x) – непрерывную и положительную на отрезке [a ; b ] . Часть плоскости, ограниченная графиком функции y = f (x) , осью

Ox и вертикальными прямыми x = a и x = b , называется криволинейной трапецией. Найдем площадь данной трапеции.

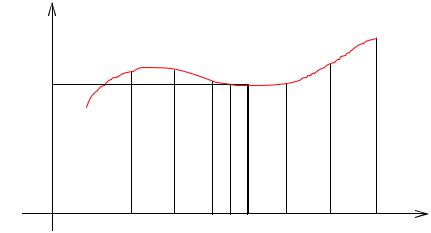
Разобьем отрезок [a ; b ] на n частей с помощью точек x0 = a < x1 < x2 < ... < xn−1 < xn = b . Проведя через точки деления прямые, параллельные оси Oy , мы разобьем данную криволинейную трапецию на n

малых криволинейных трапеций (рис. 5.1). Ясно, что площадь всей криволинейной трапеции равна сумме всех n малых криволинейных трапеций:

			n
S =	S1 +	S2 +... +	Sn = ∑ Si .	(1)

i=1

f (ξi )

−

n 1

Рис. 5.1

Но вычислить площадь этих малых трапеций так же трудно, как и площадь большой. Поступим следующим образом: в каждом из малых отрезков разбиения [ xi−1; xi ] ( i =1, 2, ..., n ) выберем произвольную точку xi−1 ≤ ξi ≤ xi

и построим в этой точке ординату кривой f (ξi ) .

Заменим теперь каждую малую криволинейную трапецию с основанием [ xi−1; xi ] прямоугольником с тем же основанием и с высотой, равной

f (ξi ) . Площадь такого прямоугольника равна f (ξi ) (xi − xi−1 ) .

Приняв площадь этого прямоугольника за приближенное значение площади малой криволинейной трапеции, получим:

Si ≈ f (ξi ) (xi − xi−1 ) .

(2)

Отсюда для площади данной криволинейной трапеции S имеем приближенное равенство:

		25
	n
S ≈	f (ξ1 ) (x1 − x0 ) +... + f (ξn ) (xn − xn−1 ) = ∑ f (ξi ) (xi − xi−1 )	(3)

i=1

Обозначим через λ наибольшую из длин отрезков разбиения:

λ= max{(x1 − x0 ); (x2 − x1 ); ...; (xn − xn−1 )}.

Суменьшением λ точность приближенной формулы (3) увеличивает-

ся. Поэтому естественно за точное значение площади S принять предел сумм

(3) при условии, что наибольшая длина отрезков разбиения				λ → 0 . Таким
образом,	n		n
	n		n
S = lim	∑ f (ξi ) (xi − xi−1 ) = lim		∑ f (ξi ) xi .	(4)
λ→0	i=1	λ→0	i=1
	i=1		i=1
§ 2. Понятие определенного интеграла
Пусть на отрезке [ a ; b ]		задана функция	f (x) . Выполним следующие
действия:

1)	с помощью точек деления x0 = a < x1 < x2 < ... < xn−1 < xn = b разобьем
	отрезок [ a ; b ] на n частей:
	[ x0 ; x1 ]; [ x1 ; x2 ]; …; [ xi−1 ; xi ]; …; [ xn−1 ; xn ];
2)	в каждом из отрезков разбиения [ xi−1 ; xi ], i =1,..., n выберем произ-
	вольную точку xi−1 ≤ ξi ≤ xi и умножим значение функции в этой точ-
	ке f (ξi ) на xi = xi − xi−1 – длину отрезка;
3)	составим сумму всех таких произведений

n
Sn = ∑ f (ξi ) xi ,	(5)

i=1

которую назовем интегральной суммой;

4)назовем наибольшую из длин отрезков разбиения [ xi−1 ; xi ] шагом разбиения и обозначим через λ .

Пусть число отрезков разбиения n неограниченно растет и λ при этом стремится к 0. Если при этом интегральная сумма Sn имеет предел J , кото-

рый не зависит ни от способа разбиения [ a ; b ] на малые отрезки, ни от выбора точек ξi в каждом из них, то это число называется определенным интегралом от функции f (x) на отрезке [ a ; b ] и обозначается

⌠

f (x) dx .

⌡

Читается: определенный интеграл от a до b от f (x) на dx .

Здесь: a – нижняя граница (предел) интегрирования, b – верхняя граница (предел) интегрирования,

f (x) – подынтегральная функция,

x – переменная интегрирования,

[ a ; b ] – отрезок (область) интегрирования.

Замечание 1. Для заданной функции и заданного отрезка [ a ; b ] мы, оче-

видно, имеем бесконечное множество интегральных сумм. Значения этих интегральных сумм зависят как от выбора точек деления x1 , x2 , …, xn−1 , так и

от выбора промежуточных точек ξi .

Замечание 2. Интегральная сумма, очевидно, не зависит от того, какой буквой обозначен аргумент данной функции. Следовательно, и ее предел, т.е. определенный интеграл, не зависит от обозначения переменной интегрирования:

b	b	b
⌠	⌠	⌠
f (x) dx = f (z) dz = f (t) dt .
⌡	⌡	⌡
a	a	a

Замечание 3. Выше мы установили тот факт, что определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции, построенной на отрезке интегрирования (геометрический смысл определенного интеграла).

При определении определенного интеграла мы исходили из предположения a < b . При a > b положим:

b	a	a
⌠	⌠	⌠
f (x) dx = − f (x) dx ,		f (x) dx = 0 .
⌡	⌡	⌡
a	b	a

В связи с определением определенного интеграла возникает вопрос, при каких условиях существует предел интегральной суммы, т.е. существует определенный интеграл.

Теорема (условие существования определенного интеграла).

Всякая непрерывная на отрезке [ a ; b ] функция интегрируема, т.е. для такой функции существует определенный интеграл.

§3. Свойства определенного интеграла

1.Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:

b	b
⌠	⌠
	[ f (x) + g(x)] dx =
⌡	⌡
a	a

f (x) dx + ⌠ g(x) dx .

⌡

Доказательство.

b		n		n
⌠		n		n
	[ f (x) + g(x)]dx = lim	∑[ f (ξi ) + g(ξi )]	xi = lim	∑[ f (ξi ) xi + g(ξi ) xi ] =
⌡	λ→0 i=1		λ→0 i=1

= lim	n	n		=
= lim	∑ f (ξi )	xi + ∑g(ξi )	xi	=
λ→0	i=1	i=1
b	b

=⌠ f (x) dx + ⌠ g(x) dx .

⌡ ⌡

	n		n
lim	∑ f (ξi )	xi + lim	∑g(ξi ) xi =
λ→0	i=1	λ→0	i=1
	i=1		i=1

2.Постоянный множитель подынтегральной функции можно вынести за знак интеграла:

b	b
⌠	⌠
k f (x) dx = k f (x) dx .
⌡	⌡
a	a

Доказательство.

b			n
⌠			n
k f (x) dx		= lim	∑k f (ξi )
⌡		λ→0 i=1
a
	n			b
= k lim	n			⌠
= k lim	∑ f (ξi )		xi	= k
λ→0	i=1			⌡

xi = lim k∑n f (ξi )

λ→0 i=1

f (x) dx .

xi =

3. Если область интегрирования [ a ; b ] разбить на две части [ a ; c ] и [ c; b ],

то

⌠

⌡

c	b
⌠	⌠	(6)
f (x) dx = f (x) dx + f (x) dx .		(6)
⌡	⌡
a	c

Доказательство.

а) Пусть a < c < b .

Т.к. предел интегральной суммы не зависит от способа разбиения [ a ; b ] и

выбора ξi , положим xk	= c . Тогда	n
n	k	n
∑ f (ξi ) xi = ∑ f (ξi ) xi +		∑ f (ξi ) xi .
i=1	i=1	i=k +1

Отсюда

lim ∑

λ→0 i=1

или

		k
f (ξi )	xi = lim	∑ f (ξi )
	λ→0	i=1
		i=1
b		c
⌠	⌠
f (x) dx = f (x) dx
⌡	⌡
a		a

xi + lim ∑ f (ξi ) xi ,

λ→0 i=k +1

+⌠ f (x) dx .

⌡

б) Формула (6) справедлива и в том случае, когда c [a ; b]. Пусть, например, c < a < b .

	b	a	b
Тогда	⌠	a) ⌠	⌠
Тогда	f (x) dx = f (x) dx + f (x) dx .
	⌡	⌡	⌡
	c	c	a
b	b	a	b	c
⌠	⌠	⌠	⌠	⌠
f (x) dx =	f (x) dx − f (x) dx = f (x) dx + f (x) dx .
⌡	⌡	⌡	⌡	⌡
a	c	c	c	a
a	c	c	c	a
		b
4. Если f (x) ≥ 0		⌠
4. Если f (x) ≥ 0	на [a ; b], то f (x) dx ≥ 0 .
		⌡
Доказательство. Т.к.		a
Доказательство. Т.к.		f (ξi ) ≥ 0 и	xi > 0 для любого i , то
		n
	Sn	= ∑ f (ξi )	xi	J = lim Sn ≥ 0 .
		i=1		λ→0
			b	b

5.Если f (x) ≥ g(x) на [a ; b], то ⌠ f (x) dx ≥ ⌠ g(x) dx .

⌡⌡

a a

Доказательство. По условию, f (x) ≥ g(x) на [a ; b], следовательно, f (x) − g(x) ≥ 0 на [a ; b], следовательно (по свойству 4),

b		св.1,2	b	b	b
⌠	[ f (x) − g(x)]dx	св.1,2	⌠	⌠	⌠
	[ f (x) − g(x)]dx	=	f (x) dx − g(x) dx ≥ 0
⌡			⌡	⌡	⌡
a			a	a	a

f (x) dx ≥ ⌠ g(x) dx .

⌡

6. Теорема (о среднем значении).

Если

f (x) –

непрерывная на

[a ; b] функция,

то существует точка

c [a ; b] такая, что

⌠

= f (c) (b − a) .

f (x) dx

⌡

Доказательство.

m = min f (x) ,

M = max

f (x) . Тогда для

Обозначим

x [a;b]

любого a ≤ x ≤ b выполняется m ≤ f (x) ≤ M . По свойству 5 имеем:

⌠

св.1

⌠

m dx ≤ f (x) dx ≤ M dx

m dx

≤ f (x) dx

≤ M dx .

⌡

⌠ dx = lim S

; S

x +1

+... +1

λ→0

⌡

<<< < Предыдущая 1 2 3 4 5 6 78 / 208 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
27.05.20193.56 Mб249КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf
#
27.05.20191.54 Mб177КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf
#
27.05.201920.05 Mб9031Письменный Д.Т. Конспект лекций по высшей математике - Полный курс.pdf

Глава V ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

§ 1. Задача о площади криволинейной трапеции

§ 2. Понятие определенного интеграла

§3. Свойства определенного интеграла