Добавил:

sutkowska92 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бухарский инженерно-технологический институт

Предмет:

Высшая математика

Файл:

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf

Скачиваний:

177

Добавлен:

27.05.2019

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2015 16 17 18 19 20 > Следующая >>>

Определение. Дифференциальные уравнения, в которых переменные можно разделить посредством умножения (деления) обеих частей уравнения на одно и то же выражение, называется дифференциальным уравнением с разделяющимися переменными.

Уравнение вида

dy = f2 (x) dx f1 ( y)

приводится к уравнению с разделяющимися переменными умножением обеих частей на f1 ( y)dx .

Уравнение вида

f1 (x) f2 ( y)dx + f3 (x) f4 ( y)dy = 0

приводится к уравнению с разделяющимися переменными делением обеих частей на f2 ( y) f3 (x) . При этом могут быть потеряны решения, обращающие

это произведение в нуль.

Пример.

Решить уравнение

x2 y2 y′+1 = y .

Решение.

Преобразуем уравнение:

x2 y

2 dy = y −1,

x2 y2dy = ( y −1)dx .

Делим обе части уравнения на x2 ( y −1) :

dy =

y −1

Переменные разделены. Интегрируем обе части уравнения:

⌠

⌠ dx

⌠

⌠ dx

dy =

2 ,

y +1 +

dx =

2 ,

+ y + ln

y −1

= −

+C .

y −1

⌡ y −1

⌡ x

⌡

⌡ x

При делении на x2 ( y −1)

могли быть потеряны решения x = 0 и y −1 = 0 (т.е.

x2 ( y −1) = 0 ). Очевидно,

y =1 – решение уравнения,

x = 0 – нет.

§ 4. Однородные дифференциальные уравнения 1-го порядка

Определение. Уравнение y′ = f (x; y) называется однородным, если функция f (x; y) может быть представлена как функция отношения своих ар-

гументов: f (x; y) = ϕ xy .

Пример 1. Уравнение		(xy − y2 )dx −(x2 − 2xy)dy = 0 однородное, т.к.
его можно записать		xy − y2		y x −( y x)2
dy	=				.
			=
dx				1− 2( y x)
		x2 − 2xy

Однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными заменой y = t x ( y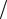x = t ), y′ = t′ x + t .

Пример 2. Решить уравнение

y′ =	xy − y2
		.
	x2 − 2xy

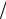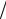Решение. Уравнение является однородным, т.к. y′ = yx −( y x)2 . 1− 2( y x)

Замена y = t x ( y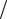 x = t ), y′ = t′ x + t приводит к уравнению:

	′	t −t 2			dt	t −t 2
t +t		x = 1	− 2t	,	dx x = 1− 2t −t ,

t −t 2		−t + 2t 2				t 2
				xdt =			dx .

xdt =	1	− 2t	dx ,		1	− 2t
	1	− 2t			1	− 2t

Разделяя переменные, получим

1− 2t dt = dx .

t 2

Интегрируем обе части полученного уравнения:

⌠1− 2t

⌠ dx

+ 2 ln

= −ln

+ ln

+ 2 ln

= ln

dt =

⌡ t 2

⌡

ln(e1 t t 2 )= ln

t 2 e1 t =

C ,

ex y = C .

§ 5. Линейные уравнения 1-го порядка

Определение.

Уравнение

y′+ p(x) y = q(x) ,

(1)

т.е. линейное относительно искомой функции и ее производной, называется линейным. Здесь p(x) и q(x) известные функции независимой переменной

x .

Чтобы его решить, надо сначала решить уравнение y′ + p(x) y = 0

(это делается путем разделения переменных) и в общем решении последнего заменить произвольную постоянную C на неизвестную функцию C(x) . За-

тем выражение, полученное для y , подставить в уравнение (1) и найти функцию C(x) .

Пример 1.	Решить уравнение
			y′+ 2xy = xe−x2 .
Решение. Решим уравнение			y′ + 2xy = 0 :						(*)
y′ = −2xy ,	dy	= −2xdx ,	⌠ dy	⌠	ln	y	= −x	2	+C ,
	dy		⌠ dy	⌠				2
	y			= − 2xdx ,
			⌡ y	⌡
			⌡ y	⌡

= ln e−x2 + ln

= ln Ce−x2 ,

y = Ce−x2

– общее решение уравнения (*).

Пусть C = C(x) . Тогда y = C(x) e−x2

– подставляем в исходное уравнение:

′

−x2

−C(x) e

−x2

2x + 2x C(x) e

−x2

= xe

−x2

′

−x2

C (x) e

′

C(x) =

2 +C .

C (x) = x ,

Таким образом, общее решение исходного уравнения:

−x2

y = e

Определение. Уравнение вида

y′+ p(x) y = q(x) yn ,

( n ≠1)

(2)

называется уравнением Бернулли.

Чтобы его решить, надо обе части разделить на

yn и сделать замену

= z . После замены получается линейное уравнение.

yn−1

Пример 2.

Решить уравнение

y′+ 2xy = 2x3 y3 .

Решение.

Разделим данное уравнение на y3 :

y′

= 2x3 .

После замены

= z получаем:

′

2 y

′

= z

= −

следовательно,

3 = −

Имеем:

z′

′

− 2 + 2xz = 2x

− z

+ 4xz

= 4x .

(**)

Решим уравнение

− z′ + 4xz = 0 .

(***)

z′ = 4xz ,

= 4xdx ,

⌠ dz

⌠

= 2x

+C ,

4xdx ,

⌡ z

⌡

= ln e2 x2

+ ln C ,

z = Ce2 x2

– общее решение уравнения (***).

Пусть C = C(x) . Тогда z = C(x) e2 x2

– подставляем в уравнение (**):

′

2 x2

−C(x) e

2 x2

4x + 4x C(x) e

2 x2

= 4x

−C

′

2 x2

−C (x) e

(x) e

4x3

⌠

⌠ 4x3

−dC(x) =

dx ,

− dC(x) =

dx .

e2 x

⌡

⌡ e2 x

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2015 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
27.05.20193.56 Mб249КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf
#
27.05.20191.54 Mб177КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf
#
27.05.201920.05 Mб9031Письменный Д.Т. Конспект лекций по высшей математике - Полный курс.pdf