0

0

S = 4S1 = 4

⌠

′

⌠

3

t 3a cos

2

t (−sin t) dt =

y(t) x (t) dt = 4

a sin

⌡

⌡

π 2

π 2

π 2

π 2

=12a2 ⌠ sin 4 t cos2 t dt =12a2 ⌠ sin 2 t sin 2 t cos2 t dt =

⌡

⌡

0

0

J =

3

a

2

π

=

3a2π

(кв.ед.).

2

4

8

8.2

Вычисление площади в полярных координатах

B

этом предположим, что ρ(ϕ) не-

Ai M

прерывная на [α; β ] функция.

Пусть радиус-вектор OA об-

i Ai−1

разует с осью l угол α , а радиус-

вектор OB – угол β . Разобьем угол

~

A

OAB на части с помощью лучей,

β

ϕi

выходящих из полюса O и обра-

O

α

l

зующих с полярной осью углы:

Рис. 5.9

α < ϕ1 < ϕ2 <K< ϕn−1 < β ;

обозначим ϕ0

=α и ϕn = β .

Обозначим точки пересечения лучей с кривой через A1 ,

A2 , …, An−1 . Криво-

линейный сектор OAB разобьется на n малых криволинейных секторов

AOA1 , A1OA2 , …, An−1OB . Углы AOA1 , A1OA2 , …, An−1OB соответственно

равны

ϕ1 =ϕ1 −ϕ0 ,

ϕ2

= ϕ2 −ϕ1 , …,

ϕn = ϕn −ϕn−1 . Если обозначить че-

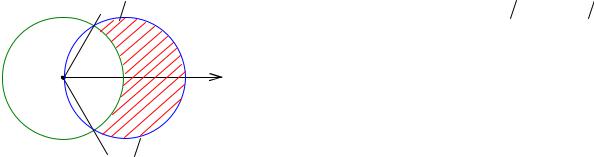
38

рез S площадь всего криволинейного сектора, а через

Si – площадь малого

криволинейного сектора, ограниченного лучами OAi−1 и OAi , то

n

S = ∑ Si .

(4)

линейного сектора. Таким образом, имеем

Si ≈

1

ρi2

ϕi . Тогда

2

n

S ≈ ∑1 ρi2

ϕi .

(5)

i=1 2

Точность этого приближенного равенства повышается с уменьшением

ϕi .

n

S = lim

∑1

ρi2

ϕi .

ϕi →0

i=1

2

1

ρ2 (ϕ) , то ее предел есть определенный интеграл, т.е.

2

β

S =

1

⌠

ρ

2

(ϕ) dϕ .

(6)

2

⌡

α

Пример 6.

Вычислить площадь фигуры, ограниченной линиями

ρ = 2 cosϕ , ρ =1

(вне круга ρ =1).

Решение. Линия

ρ = 2 cosϕ представляет собой смещенную окружность

π 3

( ρ ≥ 0

cosϕ ≥ 0 −π 2 ≤ ϕ ≤ π 2 );

линия

ρ =1 – окружность радиуса 1 с цен-

тром в полюсе (рис. 5.10). Найдем точки пе-

O

1

2 l

ресечения линий:

ρ = 2 cosϕ,

2 cosϕ =1 ϕ = ±

π

.

ρ =1,

3

−π

3