
- •ВВЕДЕНИЕ
- •Глава IV НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •§ 1. Первообразная. Неопределенный интеграл и его свойства. Теорема существования
- •1.1 Понятие первообразной и неопределенного интеграла
- •1.2 Таблица основных интегралов
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Геометрический смысл неопределенного интеграла
- •§ 2. Основные методы интегрирования
- •2.1 Интегрирование методом разложения
- •2.2 Интегрирование методом замены переменной
- •2.3 Интегрирование по частям
- •§ 3. Интегрирование простейших рациональных дробей
- •§ 4. Интегрирование дробно-рациональных функций
- •Интегрирование правильных рациональных дробей. Метод неопределенных коэффициентов
- •§ 5. Интегрирование некоторых классов тригонометрических функций
- •§ 6. Интегрирование некоторых классов иррациональных функций
- •§ 7. Понятие об интегралах, не берущихся в элементарных функциях
- •Глава V ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •§ 1. Задача о площади криволинейной трапеции
- •§ 2. Понятие определенного интеграла
- •§ 3. Свойства определенного интеграла
- •§ 4. Определенный интеграл с переменным верхним пределом интегрирования
- •§ 5. Формула Ньютона-Лейбница
- •§ 6. Замена переменной в определенном интеграле
- •§ 7. Интегрирование по частям в определенном интеграле
- •8.1 Вычисление площади в Декартовых координатах
- •8.2 Вычисление площади в полярных координатах
- •§ 9. Длина дуги плоской кривой
- •9.1 Вычисление длины дуги в Декартовых координатах
- •9.2 Вычисление длины дуги кривой, заданной параметрическими уравнениями
- •9.3 Вычисление длины дуги кривой в полярной системе координат
- •§ 10. Объем тела
- •Глава VI ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- •§ 1. Задачи, приводящие к понятию дифференциального уравнения
- •§ 3. Уравнения с разделяющимися переменными
- •§ 4. Однородные дифференциальные уравнения 1-го порядка
- •§ 5. Линейные уравнения 1-го порядка
- •§ 6. Дифференциальные уравнения высших порядков
- •6.1 Дифференциальные уравнения второго порядка
- •6.2 Дифференциальные уравнения высших порядков
- •6.3 Дифференциальные уравнения, допускающие понижение порядка
- •§ 7. Линейные дифференциальные уравнения высших порядков
- •7.1 Линейные уравнения второго порядка. Общие свойства
- •7.1.1 Линейные уравнения без правой части
- •7.1.2 Линейные уравнения с правой частью
- •7.4 Метод вариации произвольных постоянных
- •7.5 Линейные дифференциальные уравнения n-го порядка
- •§ 8. Системы дифференциальных уравнений
- •8.1 Общие определения. Нормальные системы уравнений
- •ПРИЛОЖЕНИЕ
- •Список рекомендуемой литературы
42
Пример 3.
Найти длину кривой ρ = 2sin ϕ .
Решение. Линия ρ = 2sinϕ представляет собой смещенную окружность
|
|
( ρ ≥ 0 |
|
sin ϕ ≥ 0 0 ≤ ϕ ≤ π ). Тогда длина |
||
|
2 |
искомой кривой (рис. 5.12) равна |
||||
|
|
|
β |
|
π |
|
|
|
L = |
⌠ |
ρ2 + ρ′2 |
⌠ |
sin 2 ϕ + cos2 ϕ dϕ = |
|
|
|
dϕ = 2 |
|||
|
|
|
⌡ |
|
⌡ |
|
|
|
|
α |
|
0 |
|
|
|
|
π |
|
|
|
O |
l |
= |
⌠ |
|
|
|
2 dϕ = 2π . |
|
|
||||
|
Рис. 5.12 |
|
⌡ |
|
|
|
|
|
|
0 |
|
|
|
§ 10. Объем тела
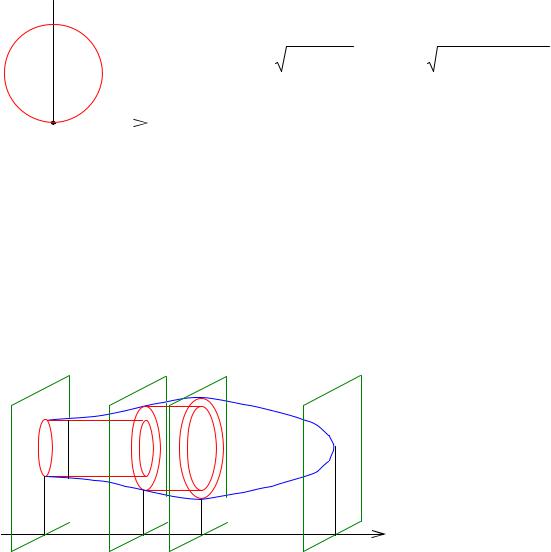
Пусть дано тело, ограниченное замкнутой поверхностью, и пусть известна площадь любого его сечения, произведенного плоскостью, перпендикулярной к некоторой прямой, например, к оси абсцисс (рис. 5.13).
При этом можно считать, что площадь такого сечения является известной нам функцией S(x) , где x – абс-
|
|
|
|
|
|
цисса точки пересече- |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ния |
указанной плоско- |
|
|
|
|
|
|
||
|
|
|
|
|
|
сти с осью x . |
|
|
x1 |
|
x2 |
|
|||
a |
|
b |
x лее, |
Предположим да- |
|||
|
|
|
|
|
|
что все тело за- |
|
|
|
Рис. 5.13 |
|
ключено между двумя |
|||
|
|
|
перпендикулярными к |
||||
оси x плоскостями, |
|
|
|
|
|||
пересекающими ее в точках a и b ( a < b ). Для опреде- |
|||||||
ления объема такого тела разобьем его на слои с помощью секущих плоскостей, перпендикулярных к оси x и пересекающих ее в точках x0 = a , x1 , x2 ,
…, xn = b . Заменим каждый слой прямым цилиндром с той же высотой и основанием, равным S(xi ) ; объем прямого цилиндра равен произведению пло-
щади его основания на высоту. Поэтому объем n -ступенчатого тела выразится суммой
n−1
Vn = S(x0 )(x1 − x0 ) + S(x1 )(x2 − x1 ) +... + S(xn−1 )(xn − xn−1 ) = ∑S(xi ) xi .
i=0
43
Предел полученной суммы, а она является интегральной суммой для функ-
ции S(x) на отрезке [a ; b], при n → ∞ и при стремлении наибольшего |
xi к |
нулю и даст нам искомый объем |
|
b |
|
⌠ |
(1) |
V = S(x) dx . |
|
⌡ |
|
a |
|
Если рассматриваемое тело получается вращением криволинейной трапеции, ограниченной линией y = f (x) вокруг оси Ox , то поперечным сече-
нием с абсциссой x служит круг, радиус которого равен соответствующей ординате линии y = f (x) . (Если y < 0 , то радиус равен y .) В этом случае
S(x) =π y2 ,
и мы приходим к формуле для объема тела вращения
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V =π |
⌠ |
, |
|
где y = f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||
|
|
|
|
|
|
y2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
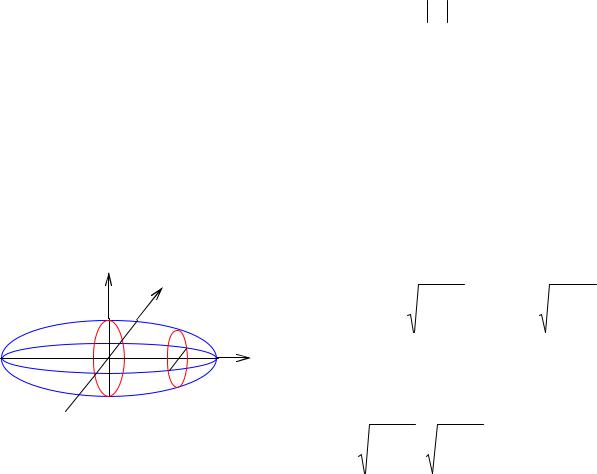
Найти объем трехосного эллипсоида |
|
+ |
|
+ |
=1. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
a2 |
|
b2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Его плоскими сечениями, |
|
перпендикулярными, например, к оси |
||||||||||||||||||||||||||||||||||||||
|
z |
|
|
|
y |
|
|
Ox (рис. 5.14), являются эллипсы с по- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 |
|
|
||||||
|
c |
|
|
|
|
|
луосями |
|
|
|
|
b |
|
1− |
|
|
|
|
|
и |
|
c 1− |
, |
|||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
a2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
− a ≤ x ≤ a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
O |
|
|
|
|
a x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Площадь S(x) поперечного сече- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ния в точке x известна: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 |
|
|
x2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x) = πb |
|
1− |
|
2 c 1− |
|
|
2 |
|
|
|
|
2 |
; |
||||||||||||||||||
|
Рис. 5.14 |
|
|
|
|
a |
a |
|
= πbc 1− |
c |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||
|
⌠ |
|
x |
2 |
|
⌠ |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
πabc . |
|
|
|
|
|
|||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
V = πbc 1− |
|
a |
dx = 2πbc 1 |
a |
dx = |
2πbc x − |
3a |
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||
|
⌡ |
|
|
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
−a |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если две из полуосей равны между собой, например, c = b , то эллипсо- |
|||||||||||||||||||||||||||||||||||||||
ид превращается в шар объема V = 4 |
πa3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
