
- •ВВЕДЕНИЕ
- •Глава IV НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •§ 1. Первообразная. Неопределенный интеграл и его свойства. Теорема существования
- •1.1 Понятие первообразной и неопределенного интеграла
- •1.2 Таблица основных интегралов
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Геометрический смысл неопределенного интеграла
- •§ 2. Основные методы интегрирования
- •2.1 Интегрирование методом разложения
- •2.2 Интегрирование методом замены переменной
- •2.3 Интегрирование по частям
- •§ 3. Интегрирование простейших рациональных дробей
- •§ 4. Интегрирование дробно-рациональных функций
- •Интегрирование правильных рациональных дробей. Метод неопределенных коэффициентов
- •§ 5. Интегрирование некоторых классов тригонометрических функций
- •§ 6. Интегрирование некоторых классов иррациональных функций
- •§ 7. Понятие об интегралах, не берущихся в элементарных функциях
- •Глава V ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •§ 1. Задача о площади криволинейной трапеции
- •§ 2. Понятие определенного интеграла
- •§ 3. Свойства определенного интеграла
- •§ 4. Определенный интеграл с переменным верхним пределом интегрирования
- •§ 5. Формула Ньютона-Лейбница
- •§ 6. Замена переменной в определенном интеграле
- •§ 7. Интегрирование по частям в определенном интеграле
- •8.1 Вычисление площади в Декартовых координатах
- •8.2 Вычисление площади в полярных координатах
- •§ 9. Длина дуги плоской кривой
- •9.1 Вычисление длины дуги в Декартовых координатах
- •9.2 Вычисление длины дуги кривой, заданной параметрическими уравнениями
- •9.3 Вычисление длины дуги кривой в полярной системе координат
- •§ 10. Объем тела
- •Глава VI ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- •§ 1. Задачи, приводящие к понятию дифференциального уравнения
- •§ 3. Уравнения с разделяющимися переменными
- •§ 4. Однородные дифференциальные уравнения 1-го порядка
- •§ 5. Линейные уравнения 1-го порядка
- •§ 6. Дифференциальные уравнения высших порядков
- •6.1 Дифференциальные уравнения второго порядка
- •6.2 Дифференциальные уравнения высших порядков
- •6.3 Дифференциальные уравнения, допускающие понижение порядка
- •§ 7. Линейные дифференциальные уравнения высших порядков
- •7.1 Линейные уравнения второго порядка. Общие свойства
- •7.1.1 Линейные уравнения без правой части
- •7.1.2 Линейные уравнения с правой частью
- •7.4 Метод вариации произвольных постоянных
- •7.5 Линейные дифференциальные уравнения n-го порядка
- •§ 8. Системы дифференциальных уравнений
- •8.1 Общие определения. Нормальные системы уравнений
- •ПРИЛОЖЕНИЕ
- •Список рекомендуемой литературы

17
§ 5. Интегрирование некоторых классов тригонометрических функций
Рассмотрим некоторые классы тригонометрических функций, интегрирование которых сводится к интегрированию дробно-рациональных функций с помощью специальных подстановок.
1. |
⌠ |
|
|
|
|
|
|
|
|
|
|
|
|
n , m – целые числа. |
|
|
|
|
|
|
|||||||||||
sinn x cosm x dx , |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
n – нечетное, в этом случае замена u = cos x ; |
|
|
|
||||||||||||||||||||||||||
|
б) |
m – нечетное, в этом случае замена u = sin x . |
|
|
|
||||||||||||||||||||||||||
|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
⌠ |
x cos4 x dx = |
|
u = cos x, du = −sin xdx, |
|
|
⌠ |
−u2 )u4du = |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
sin3 |
|
sin |
2 |
x =1 −cos |
2 |
x = |
1 − u |
2 |
= − (1 |
|||||||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌡ |
|
|
|
||||||||||||
|
⌠ |
6 |
− u |
4 |
)du = |
u7 |
− |
u5 |
= |
cos7 x |
− |
cos5 x |
+C . |
|
|
|
|
|
|||||||||||||
|
= (u |
|
|
7 |
|
5 |
7 |
|
5 |
|
|
|
|
|
|||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
⌠ sin x |
|
dx = |
|
u = cos x, |
|
|
|
|
⌠ du |
|
u−2 |
+ C |
|
1 |
|
|
+C . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
= |
|
= |
|
|
|
|||||||
|
|
|
|
|
du |
= −sin xdx |
|
|
2 |
2 cos2 |
|
||||||||||||||||||||
|
⌡ cos3 x |
|
|
|
|
|
⌡ u |
3 |
|
|
|
|
|
x |
|||||||||||||||||
Замечание. Этот же метод применим и в том случае, когда одно из чисел m или n нечетно и положительно, а другое – любое действительное число.
Пример 3.
⌠ |
3 sin2 x cos3 x dx = |
|
u = sin x, du = cos x dx, |
|
⌠ |
2 3 (1 − u2 )du = |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
cos |
2 |
x |
=1 −sin |
2 |
x =1 −u |
2 |
|
= u |
||||||||||||||||
⌡ |
|
|
|
|
|
|
|
|
|
|
|
⌡ |
|
|
|
|||||||||||
⌠ |
|
|
|
|
|
3u5 3 |
|
3u11 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
(u |
2 3 |
− u |
8 3 |
) du = |
− |
+C = |
3 |
sin |
5 3 |
|
x − |
3 |
|
sin |
11 3 |
x +C . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
5 |
|
11 |
5 |
|
|
|
11 |
|
||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определение. Многочленом относительно двух переменных u и v
называется алгебраическая сумма произведений вида Aunvm , где n и m – целые неотрицательные числа (например, u2v − 2uv + u3v − v3u +1).

18
Частное от деления двух многочленов относительно u и v называется
u2 +1
рациональным выражением относительно u и v (например, u3 − v ).
Рациональным выражением относительно функций ϕ(x) и ψ(x) назы-
вается рациональное выражение относительно u и v , в которое вместо u подставлена ϕ(x) , вместо v – ψ(x) . Рациональное выражение относительно ϕ(x) и ψ(x) принято обозначать:
|
|
R(ϕ(x),ψ(x)) . |
|
|
Пример 4. |
|
|
|
R(sin x, cos x) = |
sin x − 2 cos x |
. |
|
|
||
|
|
sin2 x + 3cos3 x |
|
2. |
⌠ |
|
|
R(sin x, cos x) dx . |
|||
|
⌡ |
|
|
Всякий интеграл такого вида можно свести к интегралу от дробно-
рациональной функции с помощью универсальной тригонометрической подстановки
|
|
|
|
|
|
|
u = tg |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dx |
|
u = tg |
x |
, x = 2arctg u, |
|
dx = |
2du |
, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
⌠ |
|
|
|
|
1+u2 |
|
|
|
|
|
|
|
|
|
|||||||||
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||
|
|
|
|
|
|
2tg(x 2) |
|
2u |
|
|
|
1 |
− tg |
2 |
(x 2) |
|
1 |
−u |
2 |
||||
|
−sin x |
|
|
|
|
|
|
|
|
||||||||||||||
⌡1 |
|
sin x = |
|
= |
, |
cos x = |
|
= |
|
|
|||||||||||||
|
|
|
|
1+ tg2 (x 2) |
1+u2 |
1 |
+ tg2 |
(x 2) |
1 |
+u2 |
|
||||||||||||
⌠2du
|
|
|
|
|
|
|
|
|
|
⌠ |
2du |
|
⌠ |
|
du |
⌠ d (u −1) |
|
|||||||||
|
|
|
1 + u |
2 |
|
|
|
|||||||||||||||||||
= |
|
|
|
|
= |
|
|
|
|
|
= 2 |
|
|
|
|
= 2 |
|
= |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
(u −1)2 |
(u −1)2 |
|||||||||||||||
|
1 |
− |
|
2u |
⌡ u2 − 2u +1 |
|
⌡ |
⌡ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
+ u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
⌡ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= 2 |
(u − |
1)−1 |
+C = |
− 2 |
|
+C = |
|
− |
2 |
|
+C . |
|
|
|
||||||||||||
|
|
−1 |
|
|
u −1 |
|
|
x |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
−1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
Следует заметить, что п.1 является частным случаем п.2. Однако решение с помощью универсальной тригонометрической подстановки во многих случаях получается довольно громоздким. Рассмотрим еще два частных слу-
19
чая п.2, когда при нахождении неопределенного интеграла рекомендуется использовать специальную подстановку, отличную от универсальной тригонометрической.
⌠
3. R(tg x) dx .
⌡
Замена u = tg x .
Пример 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
⌠ |
|
3 |
|
|
|
|
|
|
|
u = tg x, |
|
x = arctg u, |
|
|
⌠ |
|
|
|
u3 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
tg |
|
x dx = |
|
|
|
|
|
|
du |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
du |
= |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
⌡ |
|
|
|
|
|
|
|
|
|
dx = 1+u2 |
|
|
|
|
|
|
⌡ |
|
1+u |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
⌠ |
|
|
|
|
|
u |
|
|
|
|
|
|
u2 |
|
1 |
⌠ d(1+u2 ) |
|
|
|
u2 |
|
|
|
|
1 |
|
2 |
|
|
|||||||||
= |
|
u |
− |
|
|
|
|
|
|
|
du = |
|
|
|
− |
|
|
|
|
2 |
|
= |
|
|
− |
|
ln(u |
|
+1) |
+C = |
|||||||||
1+u |
2 |
|
2 |
|
2 |
+u |
|
2 |
|
2 |
|
||||||||||||||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
⌡ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
tg |
2 x |
− |
|
1 |
|
ln(tg |
2 |
x +1) |
+C = |
tg2 x |
+ |
1 |
ln |
|
cos x |
|
+C . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4.⌠ R(sin2m x, cos2n x) dx .
⌡
Замена: |
u = tg x , |
dx = |
|
|
du |
, |
|
|
|
|
|
|
|
|
|||
|
|
+ u2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
sin2 x = |
|
tg2 x |
= |
|
u2 |
|
|
, |
cos2 x = |
|
1 |
= |
|
1 |
. |
|
|
|
+ tg2 x |
|
|
|
|
|
+ tg2 x |
|
+ u2 |
|||||||
|
1 |
|
1 + u2 |
|
1 |
1 |
|
||||||||||
§ 6. Интегрирование некоторых классов иррациональных функций
Рассмотрим некоторые типы интегралов, содержащих иррациональные выражения.
|
⌠ |
m1 |
|
m2 |
|
mk |
|
|
|
1. |
R(x, (ax + b) |
n1 |
, (ax + b) |
n2 |
, ..., (ax + b) nk ) dx , |
m , |
n Ζ. |
||
|
|
|
|
|
|
|
|
i |
i |
⌡
Данный интеграл преобразуется в интеграл от рациональной функции с помощью подстановки:
ax + b = t N , где N – НОК{n , n |
, ..., n |
k |
}. |
1 2 |
|
|
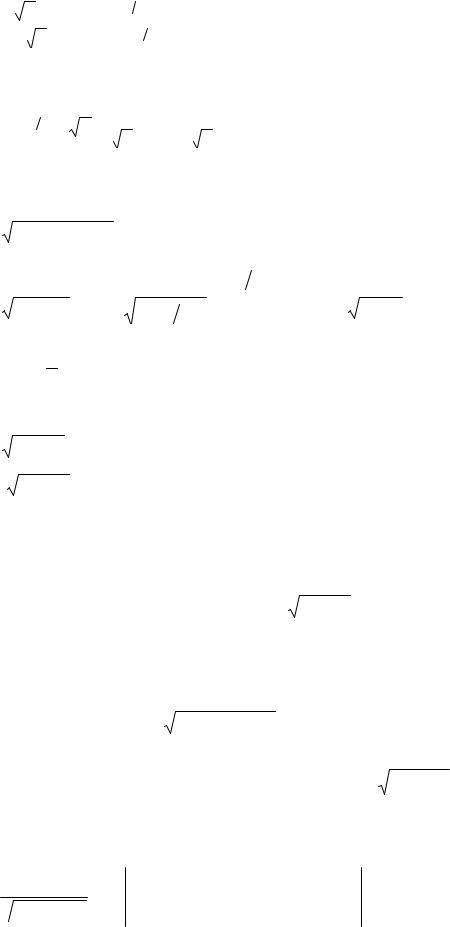
20
Пример 1. |
|
|
|
|
|
|
|
|
|
|
||
⌠ 6 x |
⌠ |
x1 6 |
|
x = t 6 , |
|
⌠ t 6t5dt |
⌠ t6 dt |
|
||||
|
|
|
||||||||||
|
|
dx = |
|
dx = |
|
|
= |
|
= 6 |
|
|
= |
|
1+ x1 3 |
dx = 6t5dt |
+t 2 |
|
+1 |
|||||||
⌡1+ 3 x |
⌡ |
|
|
⌡ 1 |
⌡ t 2 |
|
||||||
|
|
|
⌠ 4 |
|
2 |
|
|
|
|
1 |
|
|
|
t5 |
|
t3 |
|||
|
= 6 t −t +1 − |
|
|
|
|
|
|
|
− |
|
|||||||||
|
|
|
2 |
|
|
|
|
||||||||||||
|
1 + t |
dt = 6 |
5 |
3 |
|||||||||||||||
|
|
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x5 6 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
+ |
6 |
|
x −arctg |
6 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||||||
|
6 |
5 |
3 |
|
|
|
|
x +C . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
⌠ |
|
|
Mx + N |
|
|
|
dx . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ax2 + Bx +C |
|
|
|
|
|
|
|
|||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
||||||||
+ t − arctg t + C =
а)
б)
⌠ |
dx |
|
1 |
⌠ |
dx |
|
x a = u, |
|
⌠ |
du |
|
|
|
|
|
||||||||
|
|
= |
a |
|
|
= |
dx = adu |
|
= |
|
= |
|
1−(x a)2 |
|
|||||||||
⌡ |
a2 − x2 |
|
⌡ |
|
|
⌡ |
1−u2 |
|
|||
|
|
|
|
= arcsin ax +C .
⌠ |
dx |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + m |
|
|
|
|
|
|
|
|
||||
⌡ |
|
|
|
|
|
|
|
|
|
|||
|
x2 + m = −x +t, |
x2 + m = x2 − 2xt +t 2 , |
x = t 2 − m |
|||||||||
|
||||||||||||
= |
|
4t 2 |
− 2t 2 + 2m |
|
t 2 |
+ m |
|
|
|
m −t |
2t |
|
|
dx = |
dt = |
dt, |
− x +t = |
2 |
|||||||
|
|
|
4t 2 |
2t 2 |
2t |
+t |
||||||
|
|
|
|
|
|
|
|
|
||||
arcsin u +C =
, |
|
= |
= |
m +t 2 |
|
2t |
|
|
|
|
⌠ t 2 + m |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t 2 |
⌠ dt |
= ln |
|
t |
|
+C = ln |
|
x + |
x |
2 |
+ m |
|
+C . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
= |
|
|
= |
|
|
|
|
|
|||||||
m +t 2 |
|
||||||||||||||
|
⌡ t |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
⌡ |
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегралы |
вида ⌠ |
Mx + N |
dx после |
замены |
переменной |
|||
|
|
Ax2 + Bx +C |
||||||||
|
|
|
|
|
⌡ |
|
|
|
|
|
|
1 |
|
′ |
|
|
|
⌠ |
M1t + N1 |
|
|
t = |
(Ax2 |
+ Bx +C) |
|
приводятся к интегралам вида |
|
dt , вычисле- |
||||
2 |
|
pt 2 + m |
||||||||
|
|
|
|
|
|
|
⌡ |
|
||
ние которых сводится к вычислению интегралов вида а) или б).
Пример 2.
⌠ 3x + 2
⌡  x2 + x + 2
x2 + x + 2
dx = t = 0,5 (x2 + x + 2)′ = x + 0,5, = dt = dx, t −0,5 = x
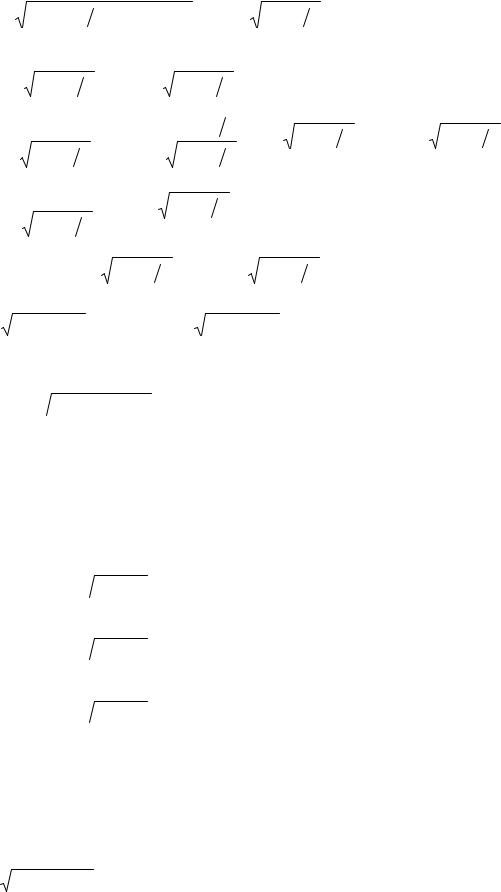
21
|
|
= |
⌠ |
3t −1,5 + 2 |
|
|
|
dt = |
⌠ |
3t + 0,5 |
|
|
dt = |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
t 2 −t +1 4 +t − |
0,5 + 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
⌡ |
|
|
|
⌡ |
t 2 + 7 4 |
|
|
|
||||||||||||||||||||||
|
|
= 3⌠ |
t |
|
dt + 1 |
⌠ |
|
dt |
|
|
|
= J . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
⌡ t 2 + 7 4 |
⌡ t 2 + 7 4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
J |
|
= |
⌠ |
|
t |
|
dt = 1 |
⌠ d (t 2 + 7 4)= |
1 t 2 + 7 4 2 |
+C = t 2 |
+ 7 4 |
+C . |
|||||||||||||||||||||
1 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
1 |
||||||||||
|
|
|
⌡ t 2 + 7 4 |
⌡ t 2 + 7 4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
J2 |
|
⌠ |
dt |
|
= ln |
|
|
t |
+ t 2 + 7 4 |
|
+C2 . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
t 2 + 7 4 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
J = 3J1 |
+ 1 J2 = 3 t 2 + |
7 4 + |
1 ln |
|
t + t 2 + 7 4 |
|
+C = |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 3 x2 + x + 2 + 1 ln |
|
x + 1 + x2 |
+ x + 2 |
|
+C . |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.⌠ R (x,  Ax2 + Bx +C )dx .
Ax2 + Bx +C )dx .
⌡
Заметим, что п.2 является частным случаем п.3.
После замены переменной t = 12 (Ax2 + Bx +C)′ данный интеграл, в за-
висимости от значений A , B и C сводится к одному из следующих интегралов:
I.⌠ R (t,  a2 −t 2 )dt ;
a2 −t 2 )dt ;
⌡
II.⌠ R (t,  a2 +t 2 )dt ;
a2 +t 2 )dt ;
⌡
III.⌠ R (t,  t 2 − a2 )dt .
t 2 − a2 )dt .
⌡
Эти интегралы находятся с помощью следующих подстановок:
I. |
t = a sin u ; |
|
II. |
t |
= a tg u ; |
III. t = |
a |
. |
|
|
|
|
cos u |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. |
|
|
|
1 |
|
|
|
|
|
|
|
⌠ |
x2 + 2x −3 |
dx = |
t = |
(x2 + 2x −3)′ = x +1, |
x = t −1, dx |
= dt, |
= |
||||
|
|
|
|
2 |
|
|
|
|
|
||
(x +1) |
3 |
|
|
|
|
|
|
||||
⌡ |
|
|
x2 + 2x −3 = t 2 − 2t +1+ 2t − 2 −3 = t 2 − 4 |
|
|
||||||
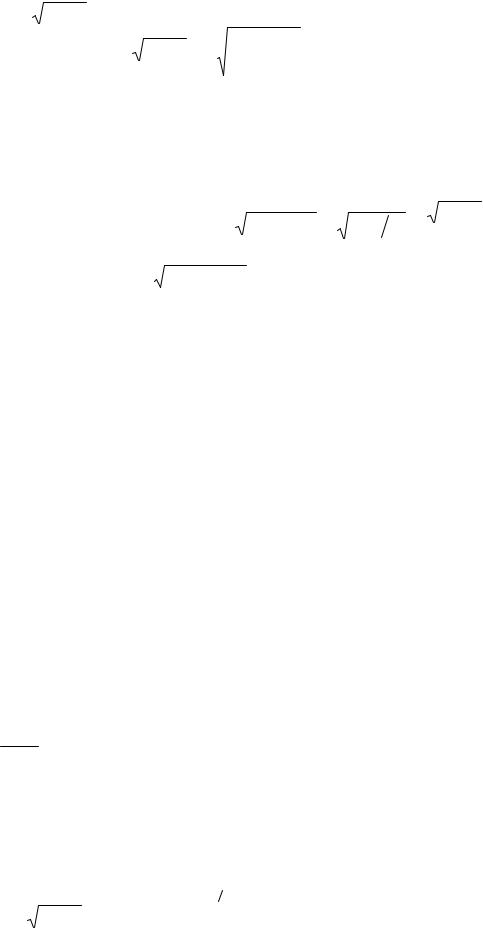
22
|
|
|
t 2 − 4 |
|
|
|
|
|
t = |
|
|
2 |
|
, |
dt = |
|
− 2 |
(−sin u) du = |
2sin u du, |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
⌠ |
|
|
|
|
|
|
cos u |
cos2 u |
|
|
|||||||||||||||||||||||||
= |
|
|
|
dt = |
|
|
|
|
|
|
|
|
|
cos2 u |
|
= |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−cos |
2 |
u |
|
|
|
|
|
|
|
|
|
||||||||
|
t |
3 |
|
|
|
|
|
|
t 2 −4 = 2 |
= 2tg u |
|
|
|
|
|
|
||||||||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 u |
|
|
|
|
|
|
|
|
|
|
|
|||
= |
⌠ |
|
2tg u cos3 u |
|
2sin u |
du = |
1 ⌠ |
|
2 |
u du = |
1 ⌠1−cos 2u |
du = |
|
|
||||||||||||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
cos |
2 |
u |
2 |
sin |
|
|
2 |
|
|
|
|
||||||||||||||
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
⌡ |
|
|
|
|
2 ⌡ |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
sin 2u |
|
|
|
|
|
|
u = arccos |
2 , |
|
cos u |
= 2 , |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= |
|
+C = |
|
|
|
|
|
|
t |
|
|
|
t |
|
|
|
|
|
|
= |
||||||||||||||||
4 |
u − |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 − 4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin u = |
1−cos2 u = |
1− 4 t 2 |
= |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
x2 + 2x − |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
arccos |
|
|
|
− |
|
|
|
(x +1)2 |
|
|
+C . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
x |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Интегрирование дифференциальных биномов
Определение. Дифференциальным биномом называется выражение
вида
xm (a +bxn )p dx ,
где m , n , p – рациональные числа.
Теорема. Интегралы от дифференциальных биномов выражаются через элементарные функции только в трех случаях:
1)p – целое число; тогда интеграл сводится к интегралу от рациональной
дроби с помощью подстановки
x= t N , где N = HOK(m, n) ;
2)m +1 – целое число; к той же цели ведет подстановка n
a +bxn = t s , где s – знаменатель дроби p ;
3) mn+1 + p – целое число; интеграл рационализируется с помощью под-
становки
ax−n +b = t s , где s – знаменатель дроби p .
Пример 4.
⌠ |
dx |
⌠ |
−1 |
3 |
|
−1 2 |
|
|
|
|
|
= x |
|
(1+ x |
) |
|
dx = |
|
1+ x3 |
|
|
|||||
⌡ x |
⌡ |
|
|
|
|
|
||
