π 3

π 3

π 3

π 3

Sкр =

1

⌠

ρ

2

dϕ

=

⌠

2 cos

2

ϕ dϕ =

⌠

sin 2ϕ

2

[1+ cos 2ϕ]dϕ = ϕ +

=

⌡

⌡

⌡

2

−π 3

−π 3

−π 3

−π 3

π

3

π

3

2π

3

.

=

+

− −

−

=

+

3

4

3

4

3

2

Sсек =

1 r 2ϕ =

1

1

2π

=

π .

2

3

2

3

Тогда

S =

2π

+

3

−

π

=

π

+

3

(кв.ед.).

3

3

3

2

2

b

⌠

′

2

(1)

l = 1+[f (x)] dx .

⌡

a

x0 = a < x1 < x2 < ... < xn−1 < xn

= b .

Построим ломаную A M1 M 2 ...M n−1 B . Длина ломаной будет равна

n

L = ∑ L1 , где

Li – длина i -го звена M i−1M i .

i=1

L = (x

i

− x

i−1

)2 + ( y

i

− y

i−1

)2 = (x

i

− x

i−1

)2 + ( f (x

) − f (x

i−1

))2 .

i

i

По теореме Лагранжа:

f (xi ) − f (xi−1 ) = f ′(ci ) (xi

− xi−1 ) ,

где xi−1 < ci < xi .

Обозначим

xi

= xi − xi−1 . Тогда имеем

Li =

xi2 +[f ′(ci ) xi ]2 = 1+[f ′(ci )]2 xi .

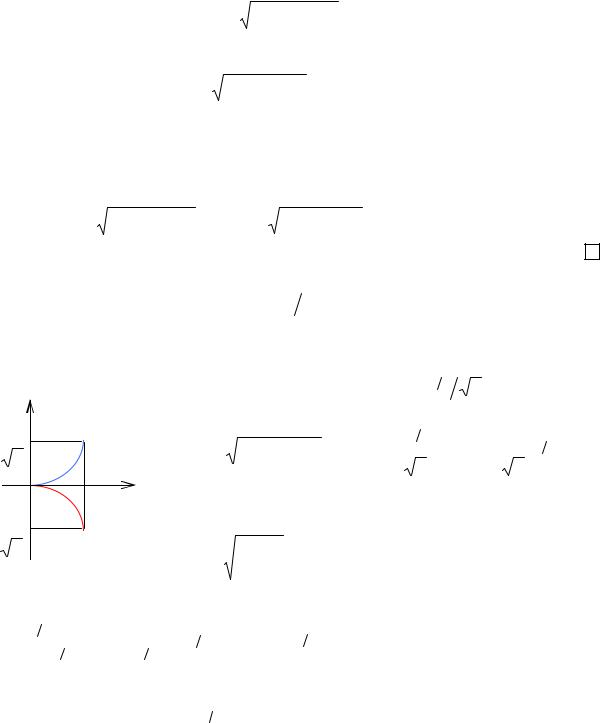
40

n

+[f ′(ci )]2

L = ∑ 1

xi .

(2)

i=1

Правая часть соотношения (2) является интегральной суммой непре-

рывной на [a ; b] функции 1+[f

′

2

≈ L .

Приближение будет тем

(x)] . AB

точнее, чем меньше шаг разбиения. Отсюда длина дуги AB будет равна пре-

b

n

xi = ⌠ 1+[f ′(x)]2 dx ,

λ = max{ x1 , ...,

xn }.

AB

= lim

∑ 1+[f ′(ci )]2

λ→0 i=1

⌡

Пример 1.

a

Найти длину дуги кривой y2 = x3 2 от x = 0 до x =1.

Решение.

График данной кривой имеет вид (рис. 5.11). Тогда искомая длина

L = 2L1 ,

где L1 – длина верхней ветви данной полукубической параболы, ко-

y

торая задается уравнением y = x3 2

2 .

1

1

⌠

′

2

x

3 2

′

3

1 2

2

L1

=

1+[f (x)]

dx =

y =

,

y

=

x

=

⌡

2

2

2

0

1

x

0

−

1

1

9

8

2

= ⌠

1+ 9 x dx =

1+ 8 x = u,

dx

=

9 du

17

=

Рис. 5.11

⌡

8

x = 0 u =1,

x =1 u =

0

8

17 8

17 8

17

3 2

=

8

⌠

1 2

du =

8

u

3 2

2

=

16

9

u

9

3

27

−1 .

⌡

1

8

1

Тогда

L

= 2L

32

17

3 2

=

−1 .

27

1

8

x = x(t),

α ≤ t ≤ β .

y = y(t),

Функции x(t) , y(t) ,

′

′

′

> 0 на [α; β ] .

x

(t) ,

y (t)

непрерывны и x

(t)

Имеем:

dy

yt′

′

f (x) = dx

=

;

xt′

′

2

yt′

2

′

′

2

′

2

dt ;

1+[f (x)] dx

= 1+

x (t) dt =

[x (t)]

+[y (t)]

xt′

b

β

⌠

′

2

⌠

′

2

′

2

AB =

dx =

+

dt .

(2)

1+[f (x)]

[x (t)]

[y (t)]

⌡

⌡

a

α

Пример 2.

x = t3

Вычислить длину дуги кривой

−t ,

y = t 2 + 2

от t = 0 до t = 3 .

β

3

3

⌠

[x

′

2

′

2

⌠

2

2

2

Решение.

L =

=

(t

−1)

+

4t

dt =

(t)]

+[y (t)] dt

⌡

⌡

α

0

3

3

t3

3

⌠

t

4

+ 2t

2

⌠

(t

2

+1) dt

= 9 +3 =12 .

=

+1 dt =

=

3

+t

⌡

⌡

0

0

0

9.3 Вычисление длины дуги кривой в полярной системе координат

Пусть кривая

задана

уравнением

в

полярных

координатах

AB

ρ = ρ(ϕ) ,

α ≤ ϕ ≤ β , причем ρ(ϕ) и ρ

′

– непрерывные на [α; β ] функ-

(ϕ)

ции.

Имеем:

x

= ρ cosϕ,

(ϕ взяли за параметр);

= ρ sin

ϕ,

y

xϕ′

= ρ′ cosϕ − ρ sin ϕ ;

yϕ′

= ρ′ sin ϕ + ρ cosϕ ;

′

2

′

2

ρ

′

2

cos

2

′

+ ρ

2

sin

2

ϕ

+ ρ

′2

sin

2

ϕ +

[xϕ ]

+[yϕ ] =

ϕ − 2ρ ρ sin ϕ cosϕ

′

2

cos

2

ϕ = ρ

′2

+

ρ .

Тогда

+ 2ρ ρ sinϕ cosϕ + ρ

β

β

[x′ ]2

+[y′

]2

dϕ =

⌠

ρ2 + ρ′2

dϕ .

(3)

AB = ⌠

ϕ

ϕ

⌡

⌡

α

α