5.4. Річна рента пренумерандо (авансовий ануїтет)

Річна рента пренумерандо (авансовий ануїтет) перед­бачає, що всі додатні, періодичні платежі цього грошового пото­ку, на відміну від звичайних рент (постнумерандо), здійснюють не наприкінці, а на початку року (авансом).

Постійну скінчену річну ренту пренумерандо з параметрами (R,n,r) з погляду розташування платежів у часі графічно відоб­ражено на рис. 5.4.

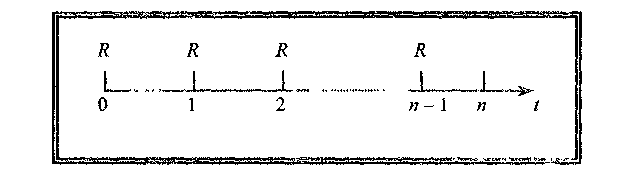
Рис. 5.4. Постійна скінчена річна рента пренумерандо

На рис. 5.4 показано, що розмір періодичних платежів R = соnst, перший платіж здійснюють в початковий (нульовий) момент часу, платежі надходять на початку періодів, тобто в останній (n-ний) момент часу платіж не здійснюють.

Порівнявши графіки виплат, наведені на рис. 5.1 та 5.4, можна зробити висновки, що фактично виплату для авансових рент здій­снюють на один період раніше, ніж для звичайних рент.

Відповідно до введених раніше позначень, запишемо вираз (5.10) для нарощеної суми п- членів авансового ануїтету:

(5.10)

Порівнявши вирази (5.3) та (5.10), можна вивести наступне співвідношення нарощених сум для звичайних та авансових рент:

(5.11)

де — нарощена сума ренти пренумерандо, — нарощена сума ренти постнумерандо.

З рівняння (5.11) видно, що для авансового ануїтету, з погляду нарахування процентів, кожний член ренти „спрацьовує” на один раз більше, ніж для звичайного ануїтету.

Врахувавши властивість (5.11) у формулі (5.4), можна записати таке рівняння для знаходження нарощеної вартості авансового ануїтету:

(5.12)

Вираз (5.12) доцільно використовувати у разі наявності довід­кових фінансових таблиць множників нарощування звичайних ануїтетів. Тоді для визначення нарощеної вартості авансового ануїтету значення з фінансової таблиці достатньо помножити на (1+r).

Розглянемо питання оцінювання теперішньої вартості авансового ануїтету. Відповідно до наведеної на рис. 5.4 схеми, приведена (дисконтована) сума п- членів скінченої ренти прену­мерандо становитиме:

(5.13)

Зрозуміло, що для авансових рент, так само як і для інших ви­дів рент, виходячи із загальної властивості грошових потоків (5.2), можна записати формулу:

(5.14)

Вираз (5.14) пов'язує між собою теперішню та кінцеву вартість авансового ануїтету.

Для визначення теперішньої вартості авансового ануїтету за відомої теперішньої вартості звичайного ануїтету, за аналогією з (5.11), можна записати співвідношення (5.15):

(5.15)

Врахувавши властивість (5.15) у формулі (5.6), можна записа­ти таке рівняння для знаходження теперішньої вартості авансово­го ануїтету:

(5.16)

Отриманий вираз (5.16) є досить складним, проте у разі наяв­ності довідкових фінансових таблиць множників дисконтування звичайних ануїтетів, для визначення теперішньої вартості аван­сового ануїтету значення з фінансової таблиці достатньо помно­жити на (1+r).