
- •Класичні фрактали
- •4.4. Завдання……………………………………………………...115
- •Множина Кантора
- •1.1 Фрактал Кантора
- •1.1.4. В е к т о р н а (арифметична) с у м а м н о ж и н к а н т о р а.
- •1.2. Теорема про множини, гомеоморфні множині Кантора
- •1.3. Застосування множин, гомеоморфних множині Кантора
- •1.4. Завдання
- •Cніжинка Коха
- •2.1. Означення сніжинки Коха
- •2.2. Властивості сніжинки Коха
- •2.3. Острівець Коха та його властивості
- •2.4. Мавпяче дерево
- •2.5. Узагальнення сніжинки Коха
- •2.6. Дослідження аналогів зірки Коха у тривимірному просторі
- •Брунькова модель,
- •Каркас брунькової моделі.
- •2.7. Кубічне узагальнення сніжинки Коха
- •2.8. Завдання
- •3.1. Килим та цвинтар Серпінського
- •3.2. Двовимірне узагальнення килима Серпінського
- •3.3. Аналоги килима Серпінського в тривимірному просторі
- •3.4. Тривимірні узагальнення килима Серпінського
- •3.5. Чотиривимірні аналоги килима Серпінського
- •3.6. Трикутний килим Серпінського, його властивості та способи задання
- •3.7. Узагальнення серветки Серпінського
- •Трикутник Паскаля за
- •3.8. Завдання
- •Крива Пеано
- •4.1. Побудова кривої Пеано
- •4.2. Відомі різновиди та узагальнення кривої Пеано
- •4.3. Узагальнення кривої Пеано на чотиривимірний та п’ятивимірний простори
- •4 Мал.2 .3.2. Узагальнення кривої Пеано на п’ятивимірний простір.
- •4.3.3. Узагальнення кривої Пеано на п-вимірний простір.
- •4.4. Завдання
1.4. Завдання
1.
Знайти функцію Кантора від числа
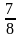 .
.
2.
Знайти функцію Кантора від числа
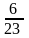 .
.
3. Утворимо таку множину з відрізка [0;1]: поділимо відрізок на 5 частин і викинемо середину, потім над відрізками, які залишилися, проробляємо таку ж операцію. Цей процес продовжимо до нескінченності. Знайти довжину викинутих відрізків. Як можна представити точки даної множини. Знайти розмірність даної множини.
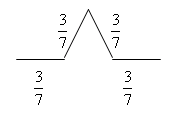
4. Утворимо таку множину на відрізку [0;1]: ділимо відрізок на 7 частин і середину заміняємо так, як це вказано на малюнку. Потім кожен з отриманих відрізків зазнає тих самих перетворень і т.д. Знайти довжину такої лінії та її розмірність.
5.
Знайти функцію Кантора
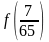 .
.
6. Визначити фрактальну розмірність фрактала, що складається з тих точок відрізка [0,1], в десятковому представленні яких відсутня цифра 4. Побудувати дану множину.
7. Визначити фрактальну розмірність фрактала, що складається з тих точок відрізка [0,1], в десятковому представленні яких відсутні цифри 4 та 6. Побудувати дану множину.
8. Визначити фрактальну розмірність фрактала, що складається з тих точок відрізка [0,1], в десятковому представленні яких відсутні цифри 3 та 7. Побудувати дану множину.
9. Визначити фрактальну розмірність фрактала, що складається з тих точок відрізка [0,1], в п’ятірковому представленні яких відсутні цифри 2 та 4. Побудувати дану множину.
10. Визначити фрактальну розмірність фрактала, що складається з тих точок відрізка [0,1], в п’ятірковому представленні яких відсутні цифри 1, 2 та 4. Побудувати дану множину.
11.
Визначити фрактальну розмірність
фрактала на площині, що складається з
точок
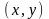 ,
де
,
де
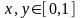 ,
причому в десятковому представленні
чисел
,
причому в десятковому представленні
чисел
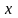 і
і
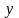 відсутні цифри 3 та 7. Побудувати дану
множину.
відсутні цифри 3 та 7. Побудувати дану
множину.
12. Визначити фрактальну розмірність фрактала на площині, що складається з точок , де , причому в десятковому представленні чисел і відсутні цифри 5 та 9. Побудувати дану множину.
13. Визначити фрактальну розмірність фрактала на площині, що складається з точок , де , причому в десятковому представленні числа відсутні цифри 2 та 7, а в десятковому представленні числа відсутні цифри 3, 5 та 8. Побудувати дану множину.
14. Визначити фрактальну розмірність фрактала на площині, що складається з точок , де , причому в системі числення за основою 5 в записі чисел і відсутні цифри 0 та 4. Побудувати дану множину.
15. Визначити фрактальну розмірність фрактала на площині, що складається з точок , де , причому в системі числення за основою 5 в записі числа відсутні цифри 1 та 3, а в записі числа відсутні цифри 0, 2 та 4.
16. Створити програму на будь-якій з мов програмування для побудови та обчислення розмінностей фракталів, описаних у завданнях 6-10.
17. Створити програму на будь-якій з мов програмування для побудови та обчислення розмінностей фракталів, описаних у завданнях 11-15.
Cніжинка Коха
2.1. Означення сніжинки Коха
Означення
1. Нехай
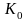 – початковий відрізок (рис 2.1). Заберемо
середню третину і додамо два нових
відрізки такої самої довжини. Назвемо
отриману множину
– початковий відрізок (рис 2.1). Заберемо
середню третину і додамо два нових
відрізки такої самої довжини. Назвемо
отриману множину
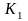 .
Повторимо цю процедуру багатократно,
на кожному кроці заміняючи середню
третину двома новими відрізками.
Позначимо через
.
Повторимо цю процедуру багатократно,
на кожному кроці заміняючи середню
третину двома новими відрізками.
Позначимо через
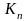 фігуру, отриману після n-го кроку.
Послідовність кривих
фігуру, отриману після n-го кроку.
Послідовність кривих
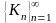 збігається до деякої граничної кривої
збігається до деякої граничної кривої
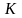 ,
яку називають сніжинкою Коха [8:17].
,
яку називають сніжинкою Коха [8:17].
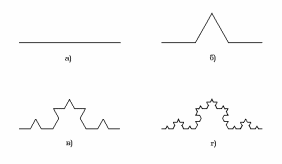
Рис. 2.1.
На рис. 2.2 показана сніжинка Коха після трьох кроків побудови.

Рис 2.2.
О
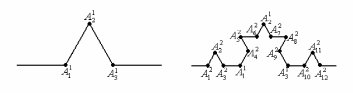
Рис. 2.3.
значення 2. Сніжинкою Коха називається крива, кожна третина якої будується ітераційно, починаючи з однієї із сторін рівностороннього трикутника. Нехай – початковий відрізок (рис 2.1). Заберемо середню третину і додамо два нових відрізки такої самої довжини. До сніжинки Коха на цьому кроці належать точки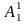 ,
,
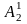 ,
,
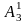 (рис. 2.3). Повторимо цю процедуру
багатократно, на кожному кроці заміняючи
середню третину двома новими відрізками.
На другому кроці сніжинці Коха крім вже
названих будуть належати точки
(рис. 2.3). Повторимо цю процедуру
багатократно, на кожному кроці заміняючи
середню третину двома новими відрізками.
На другому кроці сніжинці Коха крім вже
названих будуть належати точки
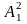 ,
,
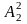 ,
,
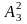 ,
,
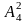 ,
,
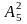 ,
,
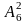 ,
,
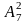 ,
,
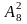 ,
,
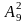 ,
,
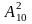 ,
,
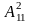 ,
,
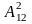 .
.
На інших сторонах рівностороннього трикутника робимо аналогічні побудови і одержуємо відповідні точки сніжинки Коха. Після нескінченної кількості кроків отримаємо зліченну множину точок, зробивши замикання якої (множина вже матиме потужність континуум) і одержимо сніжинку Коха.
Аналітичне задання. Ідея наведеного нижче способу побудови та аналітичного задання сніжинки Коха запропонована Працьовитим М.В. [23].
Означення
3. Візьмемо послідовність
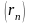 :
:
![]() і множину коренів шостого степеня з
одиниці
і множину коренів шостого степеня з
одиниці
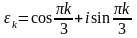 ,
,
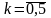 .
Кожному числу
.
Кожному числу
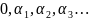 ,
яке належить відрізку [0,1] і має нескінченну
кількість цифр після коми, поставимо у
відповідність точку комплексної площини
,
яке належить відрізку [0,1] і має нескінченну
кількість цифр після коми, поставимо у
відповідність точку комплексної площини
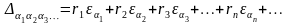 (2.1)
(2.1)
Введемо
обмеження на вибір
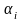 :
:
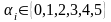 ,
коли
,
коли
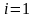 ;
;
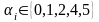 ,
коли
,
коли
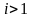 ,
причому забороняються такі комбінації
,
причому забороняються такі комбінації
 :
:
21,
22, 201, 202, 2001, 2002,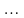 ;
45, 44, 404, 405, 4004, 4005,
(2.2)
;
45, 44, 404, 405, 4004, 4005,
(2.2)
Множина точок комплексної площини, утворена за правилом (2.1) із обмеженням (2.2) на вибір , утворить сніжинку Коха діаметром 2.
Змінюючи послідовність та групу комплексних коренів n-го степеня з 1, можна будувати різноманітні фрактали.
