4.3. Узагальнення кривої Пеано на чотиривимірний та п’ятивимірний простори

Результати даного підрозділу взято з дипломної роботи Мороз І. В. [14].

4.3.1. Узагальнення кривої Пеано на чотиривимірний простір. Ми розглянули криву Пеано розмірності 2 і 3, ознайомились також з кривою, що заповнює острівець Коха. Постає питання: а чи може дана крива заповнювати об’єкт розмірності більшої ніж 3, наприклад, розмірності 4? Для дослідження був вибраний гіперкуб, як чотиривимірний об’єкт (рис. 4.12).

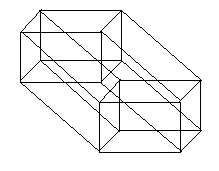
Рис. 4.12.

На першому етапі побудови кривої Пеано необхідно розбити даний гіперкуб на скінченну кількість об’єктів цієї самої природи. Наприклад на першому етапі побудови кривої Пеано, що заповнює тривимірний куб, даний об’єкт був розбитий на 8 кубиків, які в свою чергу на наступних етапах побудови також розбивались на таку саму кількість кубиків. Виявилось, що даний чотиривимірний куб на першому етапі розбивається на шістнадцять рівних гіперкубиків, кожен з яких кріпиться до однієї з вершин гіперкуба.

Далі постає завдання показати спосіб обходу кривою даного об’єкта на першому етапі. На рис.4.13 показано спосіб обходу по одному з ребер чотиривимірного куба. Крива обходить кожен з шістнадцяти гіперкубиків по одному з ребер, аналогічно великому гіперкубу. На наступному кроці кожен з шістнадцяти гіперкубиків розбивається аналогічно на таку саму кількість кубиків і крива обходить кожен з них так само, як на першому етапі, і т.д.

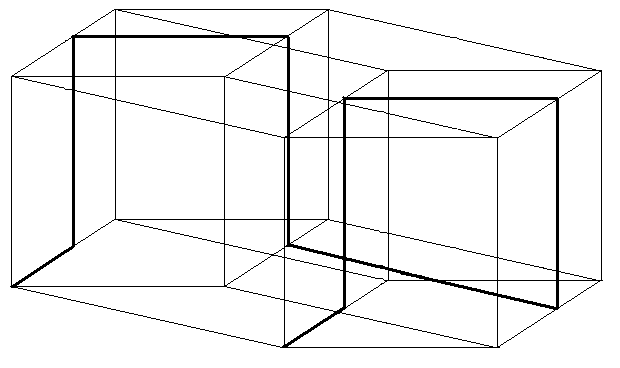
Рис. 4.13.

4 Мал.2 .3.2. Узагальнення кривої Пеано на п’ятивимірний простір.

Ми розглянули об’єкт розмірності чотири. Отже, крива Пеано може обходити об’єкти розмірності більшої ніж три. Перевірити це можна дослідивши п’ятивимірний куб. Так само, як і для інших фігур в першу чергу потрібно провести розбиття п’ятивимірного куба на рівні об’єкти подібні йому. Як виявилося тут прослідковуються певні закономірності, а саме чотирикутник розмірності 2, що має чотири вершини, на першому етапі ітерацій розбивається на чотири чотирикутники, куб, що має вісім вершин і розмірність 3 розбивається на першому етапі на вісім кубиків, гіперкуб, що має шістнадцять вершин розбивається на першому етапі на шістнадцять гіперкубиків. Отже, можна вважати, що будь-який об’єкт розмірності n на першому етапі побудови кривої Пеано можна розбити на подібних фігур.

Оскільки ми розглядаємо об’єкт розмірності 5, п’ятивимірний куб (див. рис. 4.14), то на першому етапі ітерацій його потрібно розбити на 32 кубики подібних п’ятивимірному кубу. Кожен з яких розбивається аналогічно.

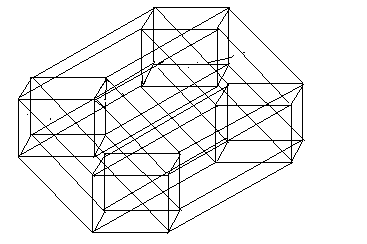
Рис. 4.14.

На рис. 4.15 показано криву Пеано для 5-вимірного куба.

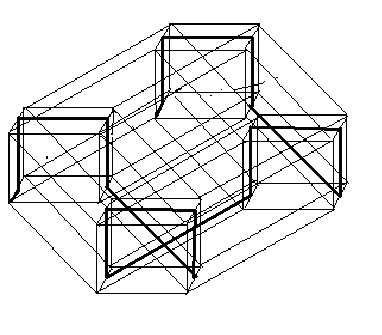
Рис. 4.15.

4.3.3. Узагальнення кривої Пеано на п-вимірний простір.

Щоб прослідкувати спосіб обходу кривої Пеано куба розмірності n, достатньо знати спосіб обходу для куба розмірності n-1, тобто прослідковується така закономірність: на першому кроці розбиття, щоб побудувати криву Пеано для куба розмірності n, достатньо обійти цією кривою (n-1)-вимірний куб. Але, обходячи останній кубик, змінити напрям обходу і перейти до іншого (n-1)-вимірного куба.

Отже, дану криву можна узагальнити на n-вимірний простір, але поки-що ми розглядали спосіб обходу по стороні, який був запропонований Гільбертом. Цікаво, а чи можна узагальнити криву, що обходить фігуру по діагоналі, тобто чи можна побудувати узагальнення для способу запропонованого Пеано (рис. 4.1)? Виявляється, що це можливо, хоча показати наочно даний спосіб обходу дещо складніше. На рис. 4.16(б) показано фрагмент 4-вимірного куба виділений жирним шрифтом рис.4.16(а). Чотиривимірний куб для даного способу побудови на першому етапі розбивається на 81 кубик (оскільки для куба розмірності 3 кількість кубиків на які розбивається фігура рівна - , то для куба розмірності 4 кількість кубиків рівна =81).

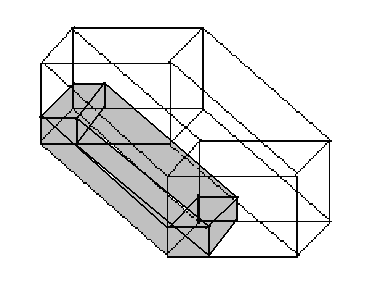
Рис. 4.16(а).

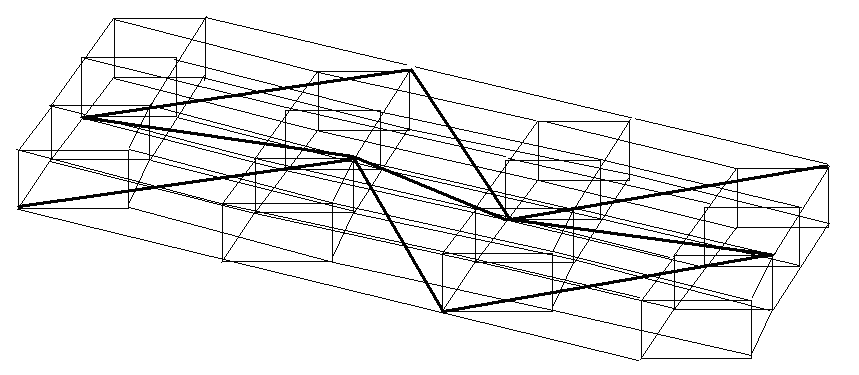
Рис. 4.16(б).

Таким способом, обходячи кожен шар, можна обійти чотиривимірний куб.

Ще однією цікавою конструкцією, є крива, що заповнює острівець Коха. Але, оскільки вже помічена закономірність, як знаючи вигляд кривої для об’єкта розмірності n-1 побудувати криву для об’єкта розмірності n, можна побудувати криву для острівця Коха, яка буде розмірності на одиницю більшої. На рис. 4.17 показано приклад такої кривої [17].

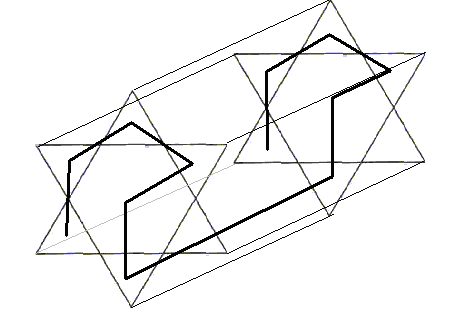
Рис. 4.17.