2.7. Кубічне узагальнення сніжинки Коха

Кубічне узагальнення – скоріше символічна назва. Точніше було б сказати, що це узагальнення за допомогою куба [10:30]. Розглянемо спосіб побудови. Ініціатором в нашому випадку слугуватиме куб зі стороною, наприклад, рівною 1. Нагадаємо, що ініціатором називається початкова фігура, об’єкт на нульовому кроці побудови (точніше визначення див. в [13:60]). Нас цікавитимуть точки куба, що лежать на серединах його ребер. Позначимо їх через а_0.1, а_0.2, а_0.3 ... а_0.12 (рис. 2.34), де для кожної а_і,j і визначимо як номер ітерації, а j – як порядковий номер точки, а множину цих точок - через А.

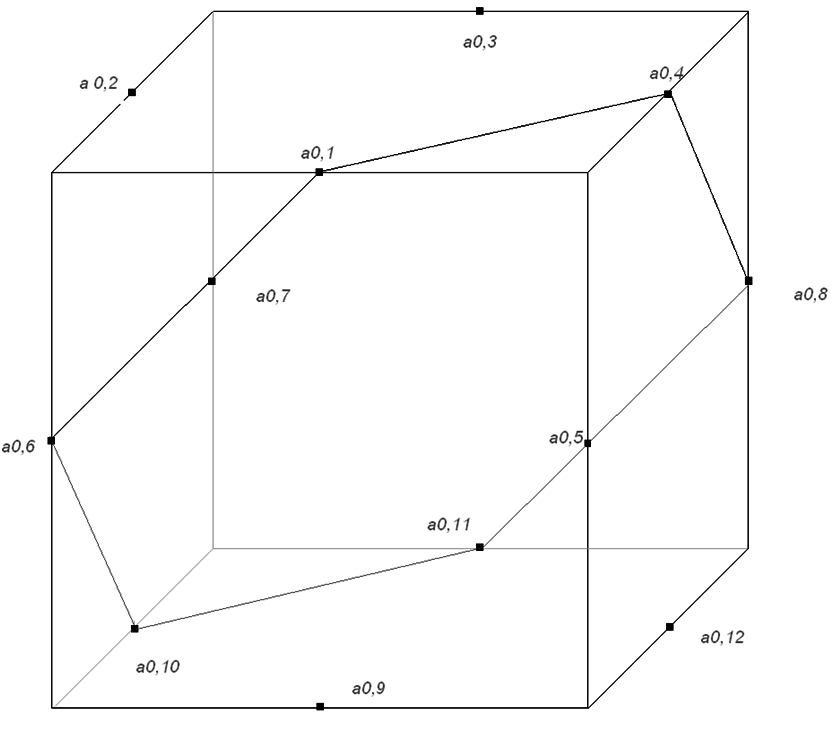
Рис. 2.34.

Через зазначені а_і,j можна провести чотири перерізи вихідної фігури, отримавши при цьому правильні шестикутники. Для наочності два з них зображено на рис. 2.35.

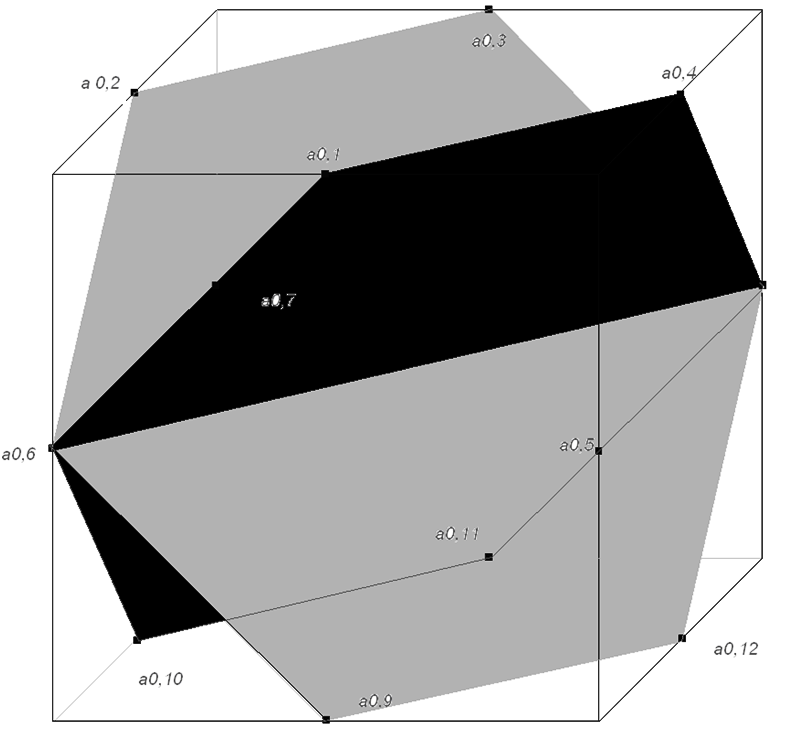
Рис. 2.35.

Розглянемо довільний з цих перерізів. Нехай, наприклад, це шестикутник з вершинами в точках а_0.1, а_0.4, а_0.8, а_0.11, а_0.10, а_0.6 (рис.2.36).

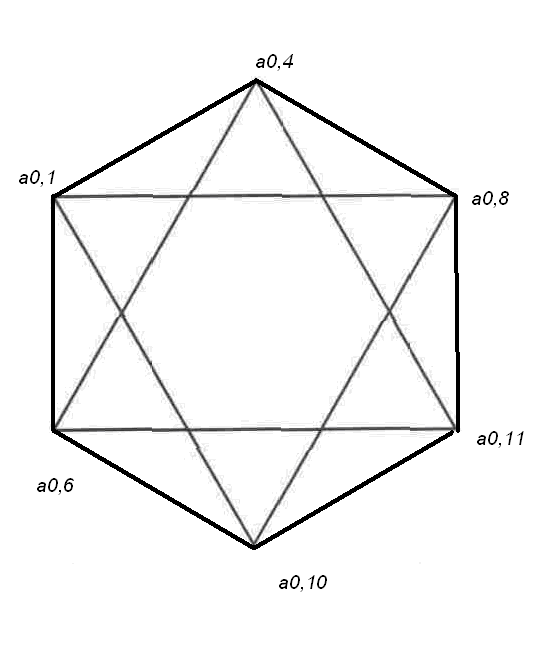
Рис. 2.36.

Зрозуміло, що в нього можна вписати зірку Коха після першого кроку її побудови. Бачимо, що вершини шестикутника вже належатимуть сніжинці Коха і після нескінченної кількості її розбудов. Але їй також належатимуть ще шість точок, які ніяк не визначені на нашій основній фігурі. Візьмемо початковий куб і розіб’ємо його на 27 кубиків, як це показано на рис. 2.37.

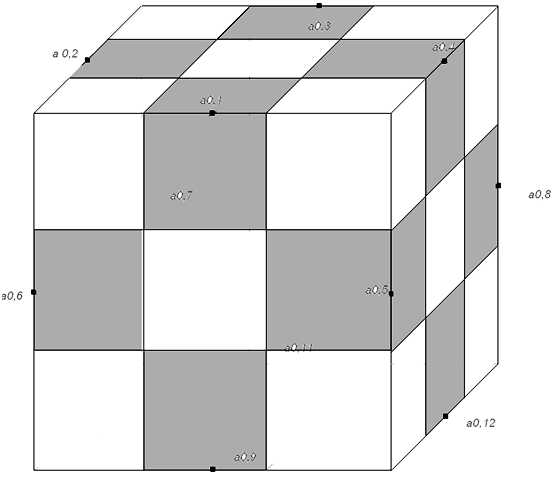
Рис.2.37.

Здійснимо перший крок розбудови – викинемо всі кубики, крім тих, які містять точки а_0.1, а_0.2, а_0.3 ... а_0.12, і позначимо через а_1,j точки, які є серединами ребер кубиків, що залишилися (рис.2.38).

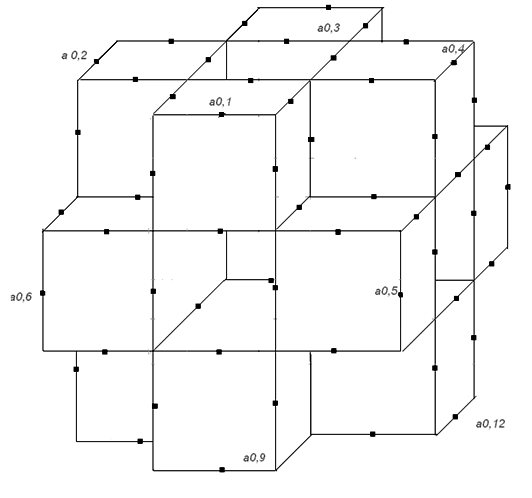
Рис. 2.38.

Зробимо переріз новоутвореної фігури по тих же точках, що й попереднього разу, тобто через а_0.1, а_0.4, а_0.8, а_0.11, а_0.10, а_0.6 (рис. 2.39).

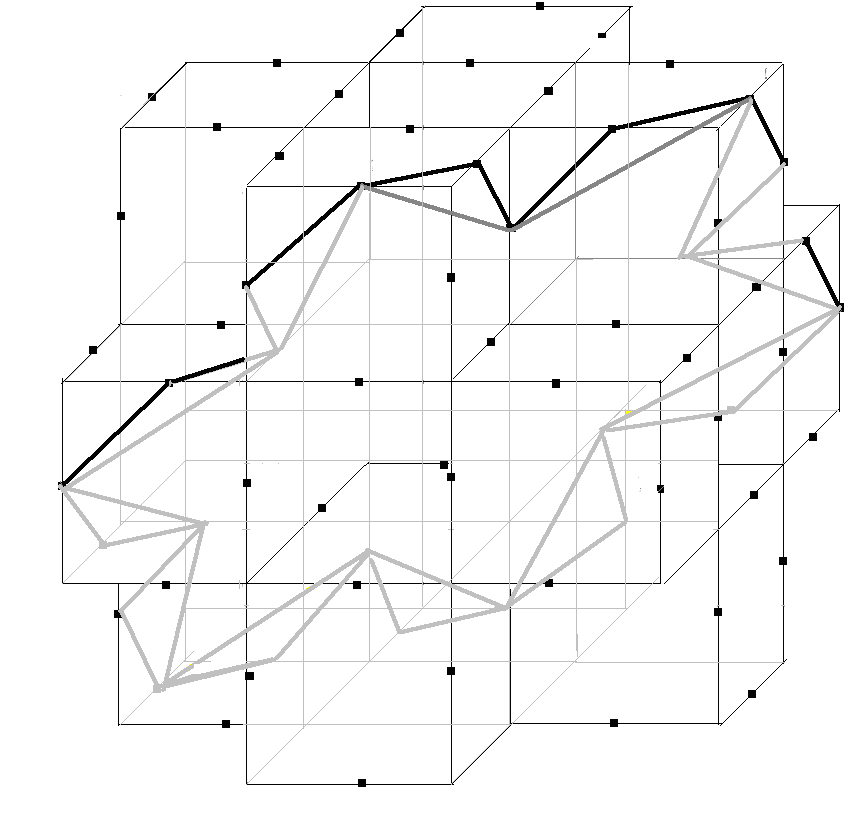
Рис. 2.39.

Тепер всі точки зірочки Коха з рис. 2.36 належать нашій множині А (рис. 2.40). Таким чином ми практично визначили спосіб точного знаходження точок тривимірного узагальнення кривої Коха.

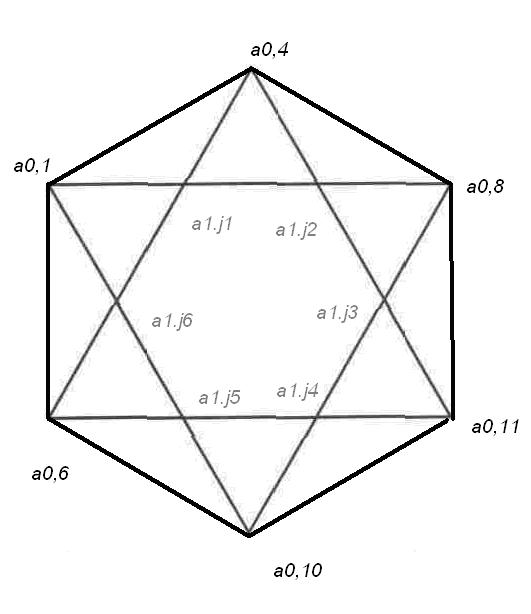
Рис.2.40.

На рисунку 2.41 представлена частина фігури після трьох ітерацій.

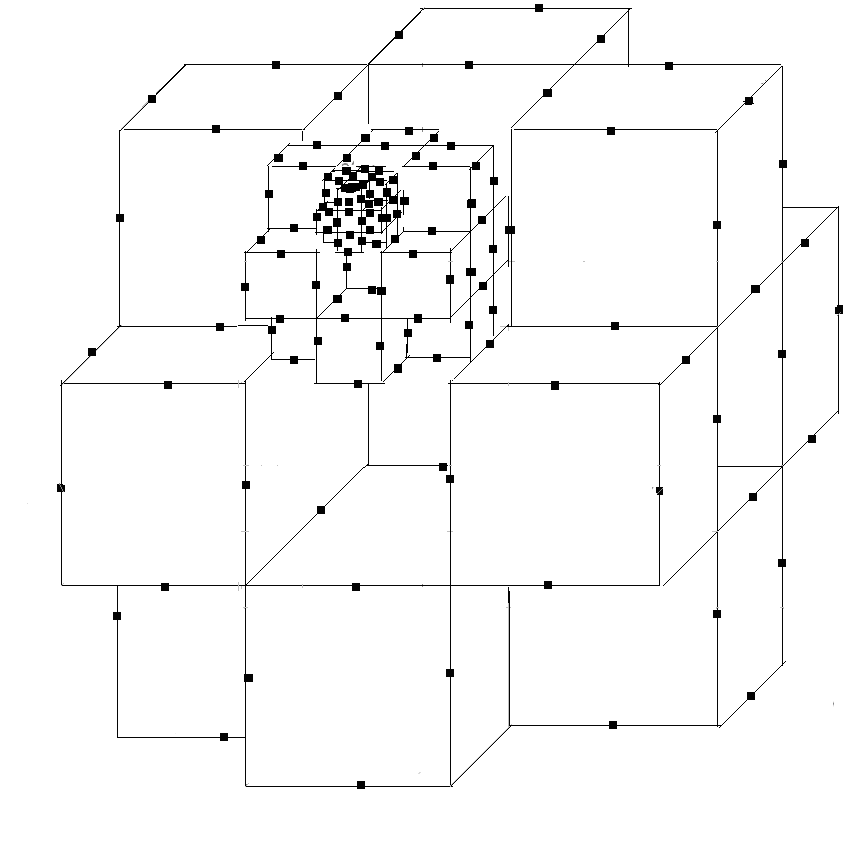
Рис. 2.41.

Постає питання, чи отримаємо ми криву Коха в перерізах при нескінченній кількості ітерацій? Звернемося до [13:71], де представлено альтернативний спосіб побудови острівця Коха, запропонований Чезаро. За ініціатор Чезаро приймає правильний шестикутник і здійснює побудову відразу з обох сторін. Розмір білих трикутничків зменшується з кожним етапом побудови, а острів Коха стає границею наближень (рис.2.42).

Рис.2.42.

Керуючись визначенням Чезаро і викидаючи квадрати запропонованим чином, ми отримаємо в границі нашого перерізу криву Коха. Крім того, в перерізах, паралельних до початкових чотирьох, буде отримуватись безліч зірочок Коха різних за розмірами.

Існує ще один спосіб розбудови куба. Користуючись рис.2.37, викинемо зафарбовані кубики разом з центральним (рис. 2.43). В такому об’єкті ми матимемо в перерізах 8 зірок Коха, попарно паралельних.

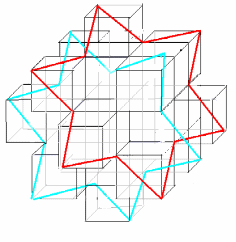
Рис. 2.43.

2.8. Завдання

1. Побудувати криву, яка проходить через кожну точку сніжинки Коха.

2. Довести, що границя сніжинки Коха має нескінченну довжину.

3. Знайти площу сніжинки Коха, яка побудована методом один трикутник всередину, два трикутники зовні.

4. Побудувати фрактали, родичі сніжинки Коха, змінивши генератор для її побудови.

5. Створити програму на одній з мов програмування для побудови сніжинки Коха та різних її родичів.

6. Створити програму на будь-якій з мов програмування для побудови сніжинки Коха, орієнтованої всередину.

7. Створити програму на одній з мов програмування для побудови аналогів сніжинки Коха в тривимірному просторі.

8. Створити програму на будь-якій з мов програмування для побудови аналогів сніжинки Коха в чотиривимірному просторі.

9. Якщо довжина кожної ланки сніжинки Коха нульового порядкудорівнює 1 см, то периметр сніжинки Коха першого порядку дорівнює

10. Кількість вершин сніжинки Коха третього порядку дорівнює?

11. Якщо S — площа трикутника, обмеженого сніжинкою Коха нульового порядку, то площа плоского многокутника, обмеженого сніжинкою Коха першого порядку, дорівнює

12. Якщо 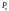— периметр сніжинки Коха n-го порядку, то які з наведених співвідношень справедливі для будь-якого цілого доданого n? Чому?

І)

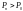
ІІ)

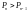
ІІІ)

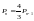
А тільки І

Б тільки ІІ

В тільки І і ІІ

Г тільки ІІ і ІІІ

Д І, ІІ, ІІІ

РОЗДІЛ 3

КИЛИМ СЕРПІНСЬКОГО