3.6. Трикутний килим Серпінського, його властивості та способи задання

Регулярний фрактал, який називають трикутним килимом або серветкою Серпінського (Sierpinski gasket), отримується послідовним вирізанням центральних рівносторонніх трикутників так, як показано на рис. 3.12. В результаті маємо фігуру, зображену на рис. 3.12, що складається з нескінченної кількості ізольованих точок. Фрактальна розмірність серветки Серпінського підраховується так:

.

Інакше килим Серпінского Т_с визначається за допомогою наступної нескінченної процедури. Візьмемо трикутник А₀, А₁, А₂, що складається з усіх його внутрішніх і граничних точок, і на першому етапі розділимо його трьома середніми лініями на чотири трикутники, про які будемо говорити, що ці трикутники рангу 1.

Видалимо внутрішність центрального трикутника рангу 1. Залишаються три трикутники, кожний з його границею. Вони попарно перетинаються між собою, усякий раз по вершині. Позначимо ці трикутники (нагадаємо, рангу 1) через 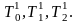Верхній індекс означає номер етапу побудови, нижній – номер вершини, до якої даний трикутник прилягає.

На другому етапі візьмемо кожен трикутник рангу 1 і розділимо його середніми лініями на чотири трикутники, які назвемо трикутниками рангу 2. Внутрішність центрального трикутника знову відкидається, а три замкнених трикутники, що залишилися, позначаються через . Перший нижній індекс і унаслідується від трикутника рангу 1, у якому знаходиться даний трикутник рангу 2. Другий індекс j означає, який із трьох трикутників рангу 2, на які підрозділяється і-й трикутник , рангу 1, мається на увазі. Числа і та j можуть приймати значення 0, 1 або 2. Помітимо, що, якщо трикутників рангу 1, що залишилося було 3, то трикутників рангу, що залишилося, 2 – вже 9 .

На наступному, третьому етапі береться рангу 2, поділяється на чотири трикутники, що являються трикутниками рангу 3. Як і раніше, внутрішність центрального викидається і три трикутники, що залишилися, позначаються через , k дорівнює 0,1 чи 2 .

Килим Серпінського – це безліч тих точок вихідного трикутника , що не належать жодному з центральних трикутників довільного рангу, тобто нескінченність, що складається з тих точок, що не відкидаються ні на якому з цих етапів(див. рис. 3.12).

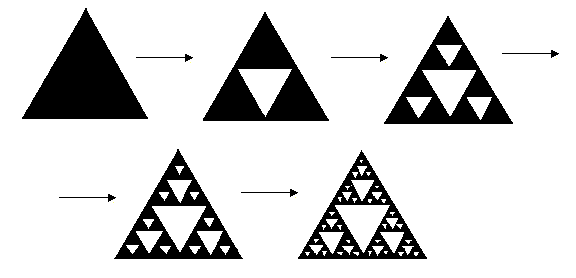
Рис. 3.12.

3.6.1. П л о щ а т р и к у т н о г о к и л и м а С е р п і н с ь к о г о. Вона дорівнює нулю. Про площу килима Серпінського говорити в тому сенсі, у якому говорять у школі про площу елементарних фігур, не можна: вона занадто “дірява” для того, щоб мати площу в змісті шкільного визначення.

З іншого боку, якщо площа вихідного трикутника А₀, А₁, А₂ дорівнює 1, а на першому кроці з нього викидається один центральний трикутник рангу 1 площі , то площа залишку . На другому етапі з кожного трикутника рангу 1, що залишились відкидається центральний трикутник. Це означає, що площа частини, що залишається після другого етапу, складає знову площі того, що залишилася після першого етапу. Легко бачити, що після кожного наступного кроку залишається площі тієї фігури, що виникла на попередньому етапі. Тобто після -го кроку площа частини, що залишилася, дорівнює 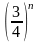. І коли ми говоримо, що «площа» килима Серпінського дорівнює нулю, ми розуміємо наступне: для кожного з можна вказати таку фігуру, що, з одного боку, її площу не перевершує , а з іншого боку, ця фігура містить килим.

Іншими словами, серветка має нульову площу, оскільки в процесі її побудови було виключено площу, що точно дорівнює площі вихідного трикутника. Про це ж говорить і значення фрактальної розмірності, яка менша за розмірність поверхні, на якій знаходиться цей об’єкт. Але серветка – це крива, всі точки якої є точками розгалуження.

3.6.2. К р и в а С е р п і н с ь к о г о. Можна побудувати неперервну лінію, яка має таке ж значення фрактальної розмірності і геометрично еквівалентна серветці Серпінського [4:21]. Ініціюючим елементом для такої побудови береться відрізок одиничної довжини, який потім замінюється на конструкцію, що називається генератором, яка складається з трьох відрізків довжиною , розміщених під кутом 120^о один до одного (рис. 3.13).

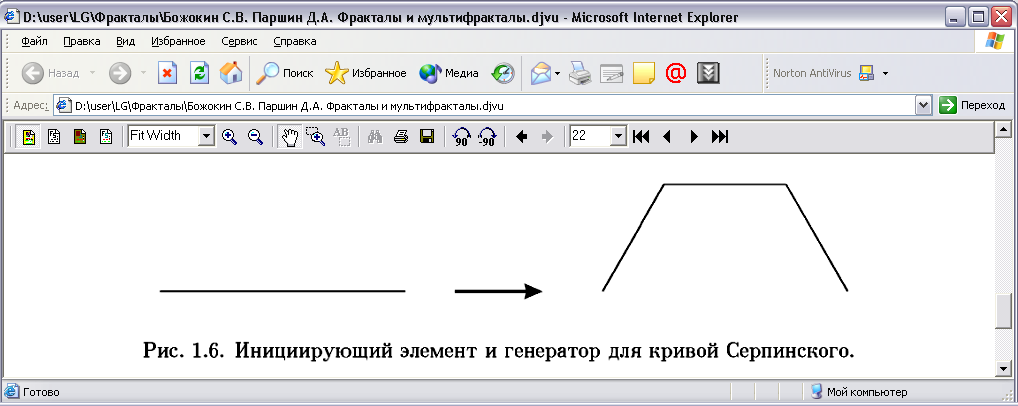
Рис. 3.13. Ініціюючий елемент та генератор для кривої Серпінського.

Потім кожен з цих відрізків замінюється в свою чергу на генератор вдвоє меншого розміру так, як показано на рис. 3.14 зліва. Права частина того ж рисунка зображає наступний крок цієї процедури.

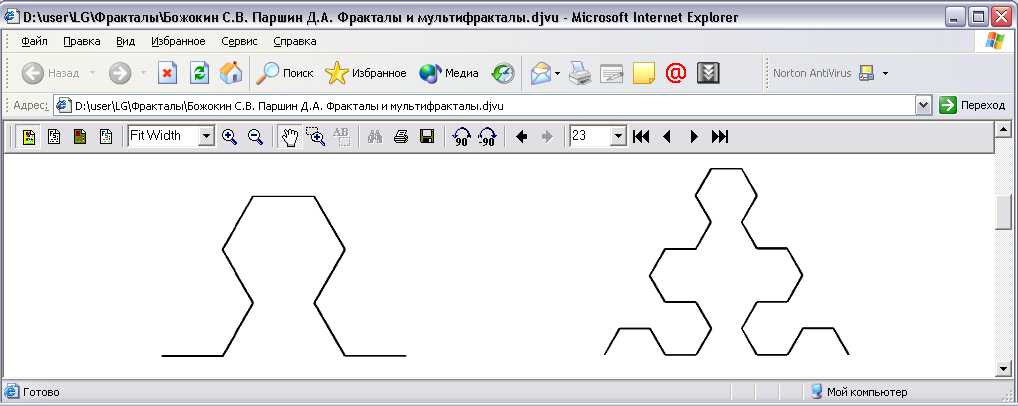
Рис. 3.14. Другий та третій кроки при побудові кривої Серпінського.

Контури майбутньої серветки Серпінського виразно проступають на наступних двох етапах (рис. 3.15).

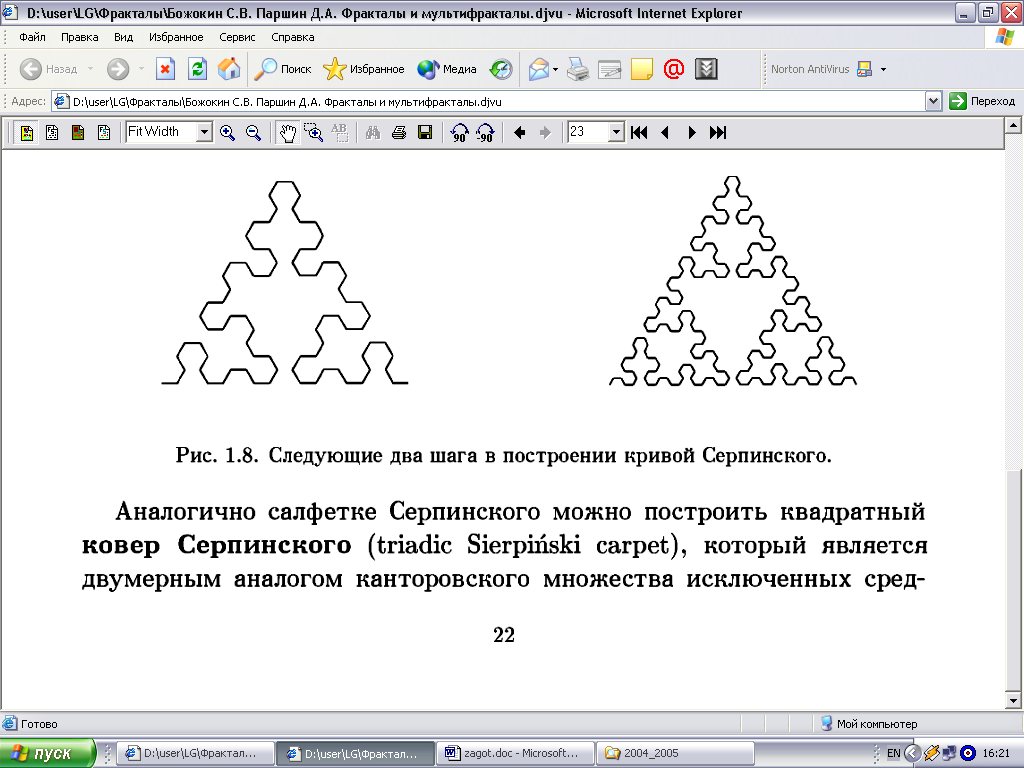
Рис. 3.15. Наступні два кроки при побудові кривої Серпінського.

Ця процедура повторюється до нескінченності. Кожне наступне зображення можна отримати з попереднього шляхом склеювання трьох зменшених вдвічі його копій, дві з яких повернуті на кут у 120^о та -120^о відносно оригіналу.

Аналітично цю множину, яку надалі позначатимемо , можна задати так:

,

де та – координати точки, взяті з одиничних відрізків в афінній системі координат, осі якої перетинаються під кутом 60^о.

Цей запис отримуємо використовуючи двійкові дроби.

3.6.3. А н а л і т и ч н і с п о с о б и з а д а н н я

Спосіб 1. Розглянемо множину SС⁽²_n⁾, отриману на n-ому кроці побудови килима Серпінського SС⁽²⁾.

Лема 1. Нехай х₀= , у₀₌ , .

M(x₀,y₀) SC⁽²⁾

Доведення леми проведемо методом математичної індукції:

1 крок : n= 1

М(x₀,y₀)

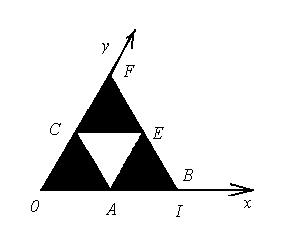
Рис. 3.16.

М( х_0, у₀) АВЕ

М(х₀ ,у₀)CEF

У загальному випадку точка

М(х₀,у₀)SC₁⁽²⁾

Отже, твердження справедливе для п =1.

2 крок: припустимо, що твердження виконується для n = k, тобто

і доведемо виконується для п = k + 1, тобто

Нехай точка М(х₀,у₀) на k-ому кроці попала в один з 3^k трикутників, її координати записуються у вигляді

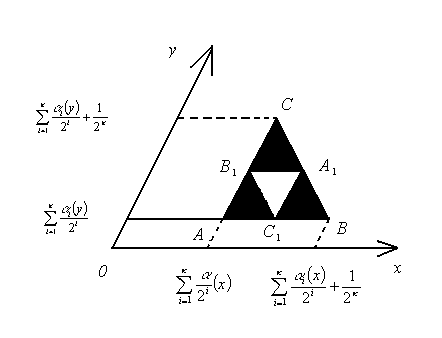
Рис. 3.17.

Розглянемо трикутник АС₁В₁. Його точки задовольняють таким умовам: всі вони лежать нижче прямої В₁С₁ та

Запишемо рівняння прямої В₁С₁:

В₁С₁ : х + у =

Тоді точка М(х₀ ,у₀)

Аналогічно, розглядаючи трикутники С₁ВА₁ та В₁А₁С маємо:

М(х_0,у₀)С₁ВА₁

М(х₀,у₀)В₁А₁С

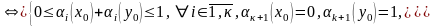
Врахувавши значення _k+1(х₀) та _k+1(у₀) у кожному з трикутників, у загальному випадку можемо записати, що точка

М(х_0,у₀)SC_k+1⁽²⁾

3 крок. Тому, за аксіомою індукції твердження правильне при кожному натуральному п. Лему доведено. [Посилання на Твердохлібову]

Теорема 3.1. Нехай х = тоді

М(х,у)SC⁽²⁾  0 _і(х)+_і(у) 1 .

Доведення. Трикутний килим Серпінського SC⁽²⁾ є перерізом усіх множин, які утворюються на першому, другому, ..., -ому, ... кроці побудови, тобто

SC⁽²⁾= = SC⁽²⁾_n.

Розглянемо множину SС⁽²_n⁾, яку отримали на -ому кроці побудови трикутного килима Серпінського, За щойно доведеною лемою 1

M(x,y) SC_n⁽²⁾

В останній системі зробимо граничний перехід, при п

М(х,y) SС⁽²⁾ 

Користуючись тим, що х= маємо:

 0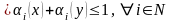 . Доведено.

Отже, розглядали одиничний паралелограм, кожна сторона якого поділена навпіл. Тоді сам паралелограм поділяється прямими на 4 менші паралелограми. Кожну точку з відрізка [0;1] можна подати у вигляді , .Отже, на першому кроці вилучаємо з розгляду точки з правого верхнього паралелограма. На другому – точки з паралелограмів, що знаходяться у правому верхньому куті паралелограмів, утворених на попередньому кроці. Продовжуючи цей процес, отримаємо точки серветки Серпінського (рис. 3.18).

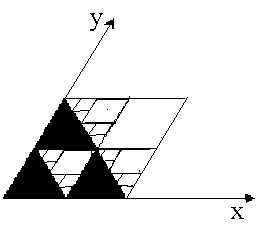
Рис. 3.18. Перші три кроки побудови серветки Серпінського.

Спосіб 2. Інший спосіб аналітичного задання серветки Серпінського пропонує Працьовитий [20] (рис. 3.19).

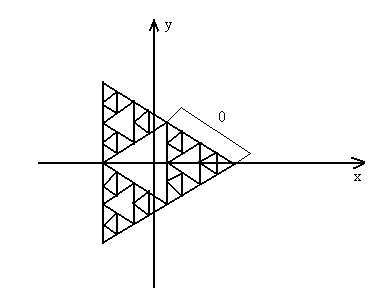
Рис. 3.19.

Для побудови трикутника Серпінського беремо ряд r_n= , групу коренів 3-го степеня з одиниці _n=cos +sin , 0,1,2…, а також точки з відрізка [0,1] в трійковій системі числення. Кожній точці з [0,1] ставимо у відповідність точку на комплексній площині, використовуючи ряд r_n та групу коренів 3-го степеня з одиниці _k. (Після коми в представленні числа беремо нескінченну послідовність цифр).

Наприклад, точка на комплексній площині, яка відповідає точці 0,0121100... визначається наступним чином:

⁽³⁾_0,0121100...=r₁₀+r₂₁+r₃₂+r₄₁+r₅₁+r₆₀+r₇₀+...= ₀+ ₁+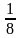 ₂+ ₁+ ₁+

+ ….

3.6.4. С а м о п о д і б н і с т ь т р и к у т н о г о к и л и м а Серпінського. Трикутний килим Серпінского самоподібний. Позначимо частину килима Серпінского, яка належить трикутнику Т¹_і , через Т_і , і= 0,1,2 . Зрозуміло, що

Т_с=Т₀ Т₁ Т₂ . (3.1)

Позначимо через h₁ перетворення гомотетії з центром у вершині А_і і коефіцієнтом гомотетії . Візьмемо одне з них, наприклад h₀ і переконаємося в тому, що при ньому килим Серпінского Т_с відображається на Т₀. Дійсно, при гомотетії 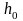трикутник Т¹_і рангу 1 переходить у трикутник Т²_0і рангу 2, і взагалі, трикутник Тⁿ_а1...аn… рангу n переходить при h₀ у трикутник Тⁿ_{0а1...аn...} рангу

Нехай точка має адресу . Їй відповідає послідовність вкладених трикутників

Т¹_а1 Т²_а1а2 ... Тⁿ_а1а2... ... (3.2)

Послідовність (3.2) при переходить також у послідовність вкладених один в одного трикутників:

Т¹₀ Т²_0а1 Т³_0а1а2 ... Т^а+n_{0а1а2...аn} ... (3.3)

Послідовності (3.3) відповідає точка х'=h₀(х), що також належить килиму. Адреса точки х' є 0а₁а₂...n....

Отже, під дією гомотетії h₀ кожна точка килима Т_с з адресою а₁а₂...n... переходить у точку килима х'=h₀(х) із Т₀ з адресою 0а₁а₂...n..., що починається з 0.

Вірне і зворотне: у будь-яку точку х' килима із Т₀, тобто в точку з адресою 0а₁а₂...n..., що починається з 0, переходить точка із наступною адресою: а₁а₂...n...

Таким чином, доведено, що h₀(Т_с)=Т₀. Тому що

Т_с=Т₀ Т₁ Т₂=h₀(Т_с) h₁(Т_с) h₂(Т_с),

килим Серпінского є об'єднання трьох гомотетичних йому образів і в цьому розумінні він самоподібний.