
- •Тема 1 випадкові величини
- •Поняття випадкової величини. Закон розподілу дискретної випадкової величини. Математичні операції над випадковими величинами 4
- •Тема 2 основні закони розподілу
- •Тема 3 елементи математичної статистики
- •Тема 4 розв’язування задач засобами mathcad 150
- •Тема 1 випадкові величини
- •Поняття випадкової величини. Закон розподілу дискретної випадкової величини. Математичні операції над випадковими величинами
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Математичне сподівання дискретної випадкової величини та його властивості
- •Розв’язування
- •Доведення
- •Доведення
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Функція розподілу випадкової величини
- •Розв’язування
- •Доведення
- •Доведення
- •Неперервні випадкові величини. Щільність ймовірності
- •Доведення
- •Розв’язування
- •Доведення
- •Розв’язування
- •Мода, медіана, квантилі, моменти випадкових величин. Асиметрія та ексцес (надвишок)
- •Розв’язування
- •Розв’язування
- •1.7 Приклади розв’язування задач
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 основні закони розподілу
- •2.1 Біноміальний закон розподілу
- •Доведення
- •2.2 Закон розподілу Пуассона
- •Розв’язування
- •2.3 Рівномірний закон розподілу
- •Доведення
- •Розв’язування
- •Розв’язування
- •2.4 Показниковий закон розподілу
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.5 Нормальний закон розподілу
- •Доведення
- •Доведення
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.6 Розподіл
- •2.7 Розподіл Ст’юдента
- •2.8 Розподіл Фішера-Снедекора
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 елементи математичної статистики
- •3.1 Варіаційні ряди, їх графічне представлення та характеристики
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.2 Поняття оцінки параметрів. Методи знаходження оцінок
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.3 Статистична гіпотеза та загальна схема її перевірки
- •Розв’язування
- •1. Перевірка гіпотез про рівність середніх.
- •Розв’язування
- •2. Перевірка гіпотез про рівність дисперсій двох сукупностей.
- •Розв’язування
- •3. Побудова теоретичного закону розподілу за експериментальними даними. Перевірка гіпотез про закон розподілу
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 розв’язування задач засобами MathCad
- •Розв’язання
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Словник основних математичних термінів, що зустрічаються в тексті
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
Розв’язування
Визначимо сподівану норму прибутку для кожного виду акцій:
![]() ;
;
![]() ;
;
![]() .
.
Визначимо дисперсію (варіацію) норм прибутку кожного виду акцій за формулою (1.15):
![]() ;
;
![]() ;
;
![]() .
.
Обчислимо середні квадратичні відхилення від сподіваних норм прибутків кожної акції:
![]() ;
;
![]() ;
;
![]() .
.
Обчислимо величину ризику для кожного виду акцій:
![]() ;
;
![]() ;
;
![]() .
.
З одержаних
результатів зрозуміло, що потрібно
вибрати акцію виду
![]() ,
оскільки для неї ризик найменший.
,
оскільки для неї ризик найменший.
Функція розподілу випадкової величини
До цих пір ми розглядали закон розподілу випадкової величини, як ряд розподілу або формулу, що дозволяє знаходити ймовірності довільних значень випадкової величини . Однак такий опис не є універсальним, оскільки його неможливо застосувати до неперервної випадкової величини, яка має нескінченну незчисленну множину можливих значень.
Для опису закону
розподілу випадкової величини можливо
розглядати не ймовірності подій
![]() для різних
для різних
![]() ,
а ймовірності події
,
а ймовірності події
![]() ,
де
– поточна змінна. Зрозуміло, що ймовірність
,
де
– поточна змінна. Зрозуміло, що ймовірність
![]() буде деякою функцією від змінної
.
буде деякою функцією від змінної
.
Функцією розподілу
(function
of
distribution)
випадкової величини
називається ймовірність того, що
випадкова величина
набуде значення меншого за
.
Позначають функцію розподілу
![]() ,
тобто
,
тобто
![]() . (1.17)
. (1.17)
Функцію іноді називають інтегральною функцією розподілу або інтегральним законом розподілу.
Приклад 1.10 Дано ряд розподілу випадкової величини
:
|
1 |
4 |
5 |
7 |
|
0,4 |
0,1 |
0,3 |
0,2 |
Знайти та графічно зобразити її функцію розподілу.
Розв’язування
Будемо задавати різноманітні значення та знаходити для них .
Якщо
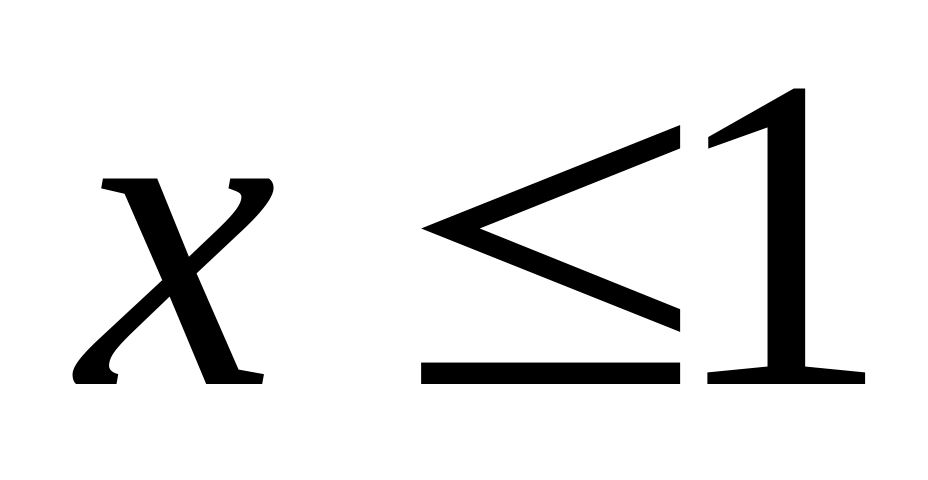 ,
то зрозуміло, що
,
то зрозуміло, що
 .
.Якщо
 ,
то
,
то
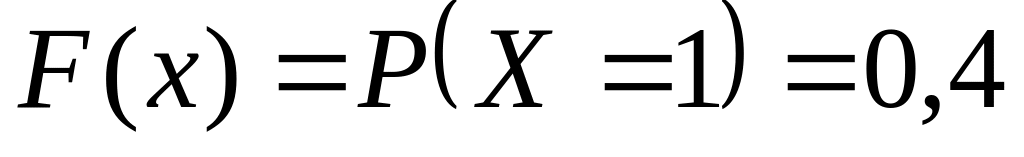 .
Зрозуміло, що і
.
Зрозуміло, що і
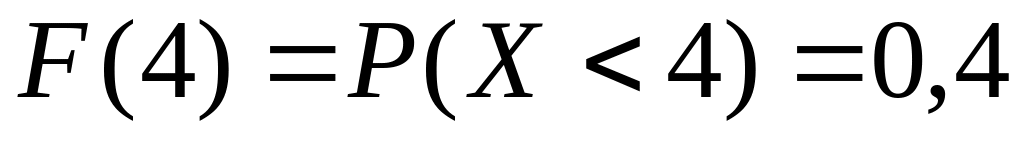 .
.Якщо
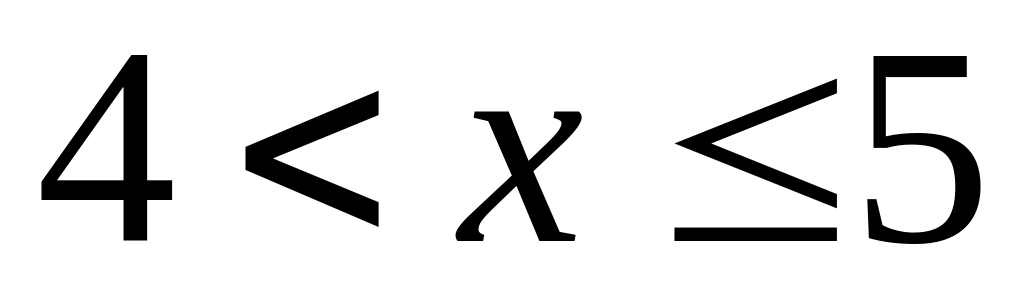 ,
то
,
то
 .
.Якщо
 ,
то
,
то
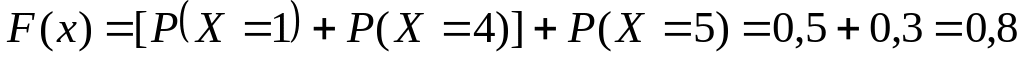 .
.Якщо
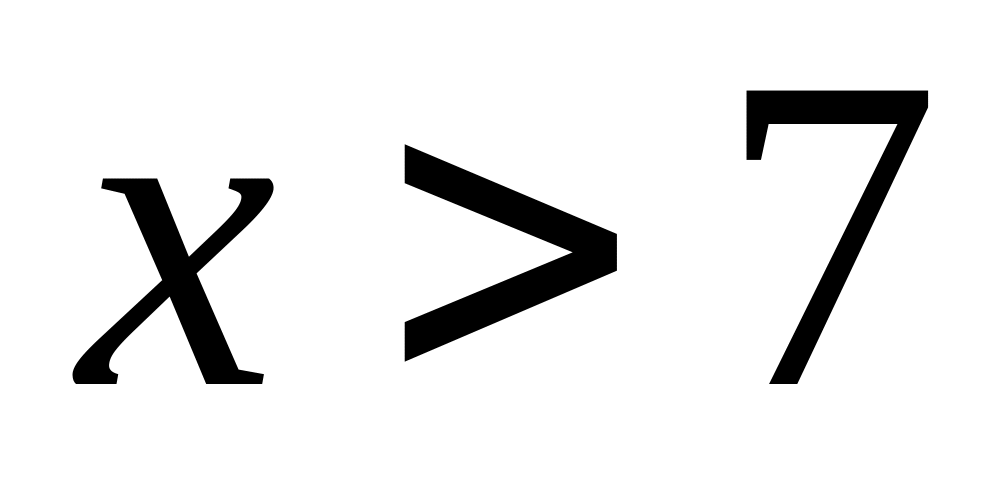 ,
то
,
то

![]() .
.
Графічно зобразимо функцію (рис. 1.4).
Маємо:
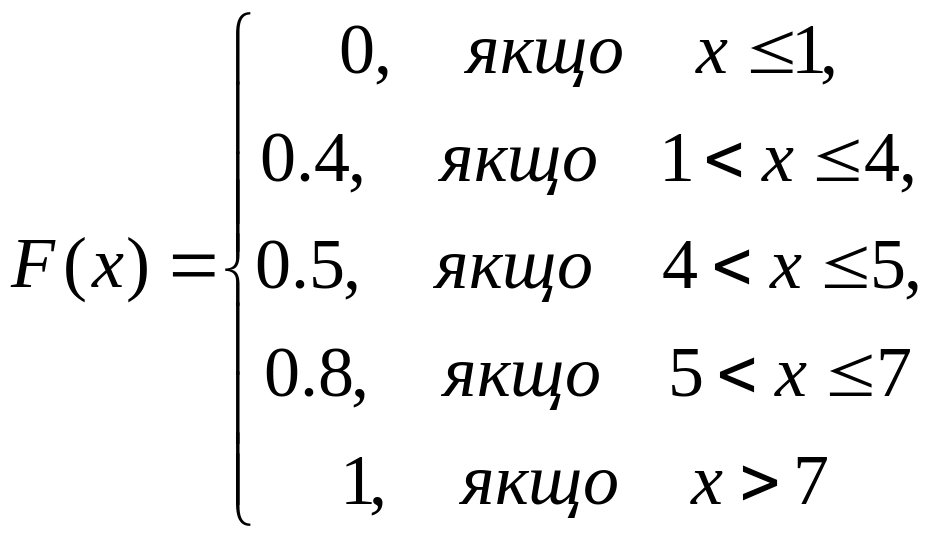
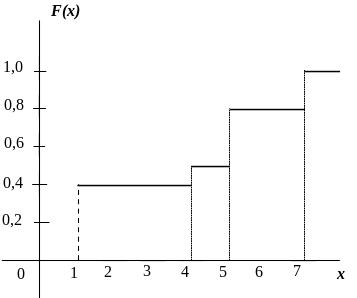
Рисунок 1.4
Зауваження. З попереднього приклада зрозуміло, що функція розподілу довільної дискретної випадкової величини є східчастою функцією, стрибки якої відбуваються в точках, що відповідають можливим значенням випадкової величини і дорівнюють ймовірностям цих значень. Сума усіх стрибків функції розподілу дискретної випадкової величини дорівнює 1.
Розглянемо загальні властивості функції розподілу.
1. Значення функції розподілу належать відрізку [0, 1].
Дане твердження випливає з того, що функція розподілу – це ймовірність.
2. Функція розподілу є неспадною на всій числовій осі.
Доведення
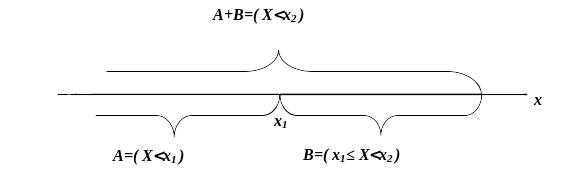 Нехай
та
– деякі точки числової осі, причому
Нехай
та
– деякі точки числової осі, причому
![]() .
Розглянемо дві несумісні події
.
Розглянемо дві несумісні події
![]() та
та
![]() .
Тоді
.
Тоді
![]() .
Це співвідношення між подіями випливає
з їх геометричної інтерпретації (рис.
1.5).
.
Це співвідношення між подіями випливає
з їх геометричної інтерпретації (рис.
1.5).
Рисунок 1.5
За теоремою додавання
![]()
або ![]() ,
,
звідки
![]() . (1.18)
. (1.18)
Оскільки ймовірність
![]() ,
то
,
то
![]() ,
тобто
– неспадна функція.
,
тобто
– неспадна функція.
3. На мінус нескінченності функція розподілу дорівнює нулю, на плюс нескінченності дорівнює одиниці, тобто
![]() ,
,
![]() .
.
