Тема 4 розв’язування задач засобами MathCad

Зауваження: Необхідно відмітити, що MathCad будуючи графік зображення ступінчастих функцій з’єднує відрізком прямої значення функцій в точках розриву. Розривні функції зображають – відмічаючи стрілкою напрям розриву ( стрілка вправо – функція неперервна в точці справа, стрілка вліво – для точок де функція неперервна зліва).

Приклад 4.1 За даними багаторічних статистичних досліджень відомо, що ймовірність народження хлопчика дорівнює 0,515. Скласти закон розподілу випадкової величини Х – кількості хлопчиків в сім’ї із 4 дітей. Знайти математичне сподівання і дисперсію цієї випадкової величини.

Розв’язання

р: = 0.515

q: =1– p

q =0.485

k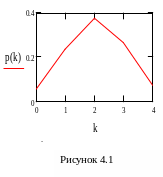 : = 0..4

Закон розподілу

p(k)

0.055

0.235

0.374

0.265

0.07

Функція розподілу випадкової величини

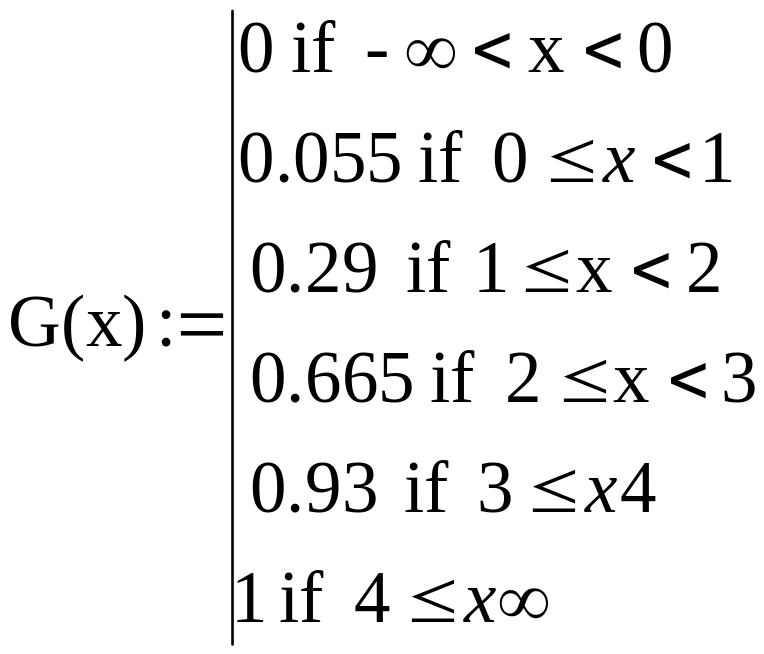
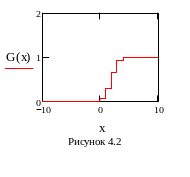
Математичне сподівання.

n: = 4

p: = 0.515

M:= n p

M = 2.06

Дисперсія

D: = n p q

D = 0.999

Приклад 4. 2. Побудуйте біноміальний розподіл для серії із 25 незалежних випробувань з ймовірністю успіху . Побудуйте многокутник розподілу і графік функції розподілу. Для знайдіть значення k, для якого величина максимальна. Перевірте рівність . Обчисліть ймовірність попадання значення випадкової величини в проміжок (1;5).

Розв’язування

Зауваження: В MathСad для обчислення щільності ймовірності і функції розподілу випадкової величини, яка має Пуасонівський розподіл, використовують функції і , значення яких – відповідно і .

k: =0..25

P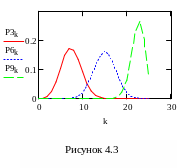 3_k: = dbinom (k, 25, 0.3)

F3(k): = pbinom (k, 25, 0.3)

P6_k: = dbinom (k, 25, 0.6)

F6(k): = pbinom (k, 25, 0.6)

P9_k: = dbinom (k, 25, 0.9)

F9(k): = pbinom (k, 25, 0.9)

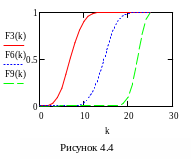
Для знайдемо значення k, величина якого максимальна.

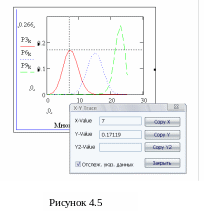З ауваження: Для того, щоб визначити за графіком розподілу найімовірніше значення випадкової величини необхідно ввійти в пункт меню Формат/ Графики/ Трассировка встановити маркер на точці максимуму розподілу і вивести в робочий документ ймовірність значення, яке вказане в вікні X–Value(Величина Х). Для досліджуваної величини найімовірніше значення дорівнює 7, ймовірність події якого дорівнює 0,17.

Фрагмент робочого документу, який містить обчислення наведено на рисунку 4.5.

Перевіримо рівність .

Ймовірності попадання значення випадкової величини в проміжок (1;5) з відповідними ймовірностями успіху дорівнюють:

F3(5) – F3(1) = 0.192

F7(5) – F7(1) =

F9(5) – F9(1) = 0

Приклад 4.3 Радист викликає кореспондента. Кожний наступний виклик проводиться лише в тому випадку, якщо попередній виклик не пройшов. Ймовірність того, що кореспондент прийме виклик дорівнює 0,4. Скласти закон розподілу числа викликів, якщо викликів не більше 5, обчислити математичне сподівання і дисперсію.