Розв’язування

За формулою (3.6) маємо для інтервального ряду

,

де числа 97, 103, … , 133, 139 – середини відповідних інтервалів.

Розглянемо властивості середньої арифметичної.

1. Якщо всі варіанти збільшити (зменшити) в одне і те ж число разів, то середня арифметична збільшиться (зменшиться) в стільки ж разів: .

2. Якщо всі варіанти збільшити (зменшити) на одне і те ж число , то середня арифметична збільшиться (зменшиться) на те ж число с:

.

3. Сума добутків відхилень варіант від середньої арифметичної на відповідні їм ваги рівна нулю:

.

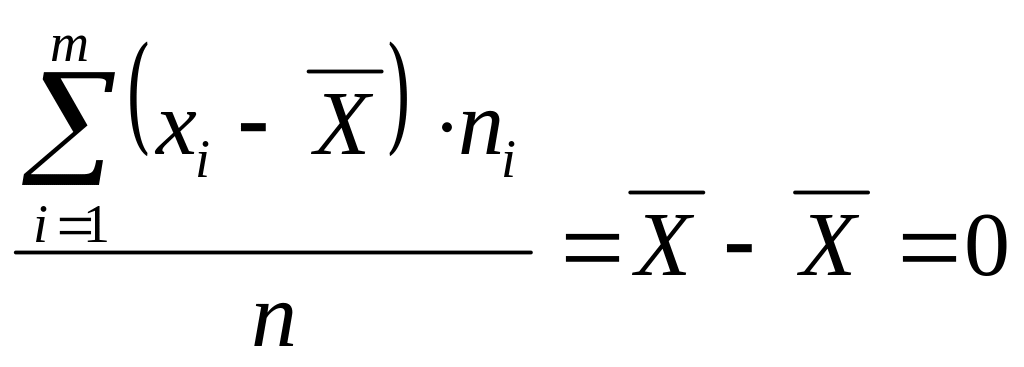4. При збільшенні і зменшенні ваг в одне і те ж число разів середня арифметична не змінюється:

.

5. Якщо кожне значення ознаки є сумою (різницею) значень ознак і , то середня арифметична ознаки рівна сумі (різниці) середніх арифметичних ознак і :

.

6. Якщо ряд складається з декількох груп, загальна середня дорівнює середній арифметичній групових середніх, причому вагами є об’єм груп:

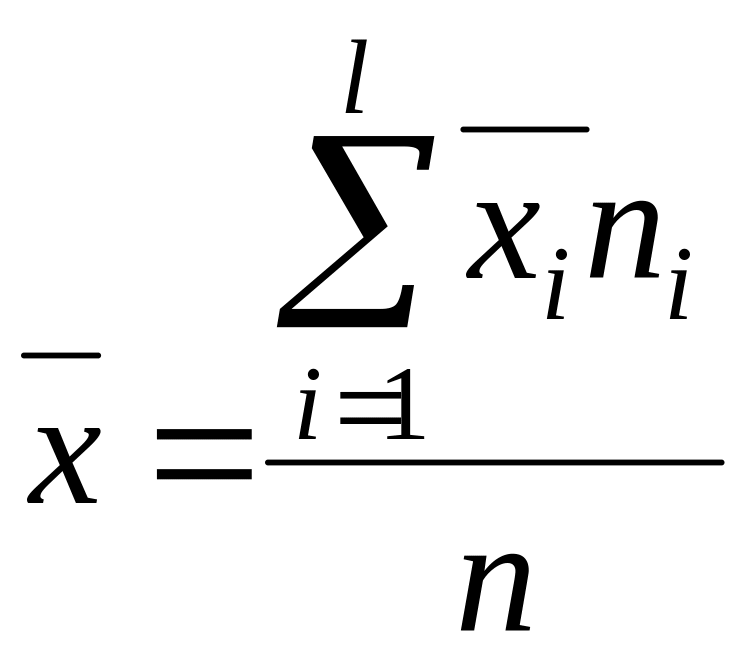, (3.7)

де – загальна середня;

– групова середня -ої групи, об’єм якої дорівнює ;

– кількість груп.

Наведені властивості приводять до спрощеної формули:

. (3.8)

Дисперсією варіаційного ряду називається середня арифметична квадратів відхилень варіант від їх середньої:

. (3.9)

Середнім квадратичним відхиленням називається арифметичне значення кореня квадратного з дисперсії:

. (3.10)

Вкажемо основні властивості дисперсії.

1. Якщо всі варіанти збільшити (зменшити) в разів, то дисперсія збільшиться (зменшиться) в разів, а середнє квадратичне значення – в разів.

2. Якщо варіанти збільшити чи зменшити на одну і ту ж постійну величину, то дисперсія не зміниться.

3. Якщо ваги збільшити чи зменшити в одне і те ж число разів, то дисперсія не зміниться.

4. Дисперсія відносно середньої арифметичної дорівнює дисперсії відносно довільної постійної без квадрату різниці між середньою арифметичною і цією постійною:

(3.11)

5. Дисперсія дорівнює середній арифметичній квадратів варіант без квадрату середньої арифметичної:

. (3.12)

6. Якщо ряд складається з декількох груп спостережень, то загальна дисперсія дорівнює сумі середньої арифметичної групових дисперсій та між групових дисперсій:

. (3.13)

Наведені властивості приводять до спрощеної формули:

. (3.14)

Коефіцієнтом варіації ( ) називається відношення середнього квадратичного відхилення до середнього виражене у відсотках (або частці одиниці):

. (3.15)

Середня арифметична та дисперсія варіаційного ряду є частинними випадками більш загального поняття – моментів варіаційного ряду.

1. Початкові статистичні моменти -го порядку:

, . (3.16)

Тоді при:

, ;

, - середня арифметична;

, - середнє квадратичне відхилення;

, .

2. Центральні статистичні моменти -го порядку:

, . (3.17)

Тоді при:

, ;

, ;

, - статистична дисперсія;

, ;

, .

Асиметрія вибіркового розподілу обчислюється за формулою . Якщо розподіл симетричний, то . Ексцесс вибіркового розподілу визначається за формулою .

Середні арифметичні розподілу ознаки в генеральній та вибірковій сукупностях називають відповідно генеральною та вибірковою середніми, а дисперсії цих розподілів – генеральною та вибірковою дисперсіями. Всі формули зведемо в таблицю.

Таблиця 3.5

Найменування характеристики	Генеральна сукупність	Вибірка
Середня
Дисперсія
Частка

Приклад 3.3 Є такі дані стосовно середніх та дисперсіях заробітної плати двох груп працівників:

Група робітників	Кількість робітників	Середня заробітна плати робітника в групі (грн.)	Дисперсія заробітної плати
Робітники, що працюють в одному відділі	40	2400	180000
Робітники, що працюють у двох відділах	60	3200	200000

Знайти загальну дисперсію розподілу робітників по заробітній праці та його коефіцієнт варіації.