11.4 Дифференциальное уравнение энергии

В основе уравнения энергии лежит закон сохранения энергии. Рассмотрим элемент массы, мгновенно заменяющий объём dxdydz с центром в точке (x, y, z).

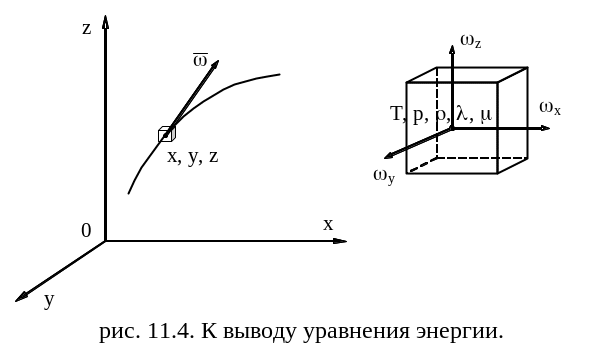
Элемент массы проходит через точку (x, y, z) со скоростью . Скорость изменения температуры определяется полной (субстанционной) производной

. (11.16)

Скорость изменения накопленной в элементе энергии (скорость накапливания) является произведением теплоёмкости С, массы dxdydz и скорости изменения температуры, т.е.

.

Скорость накапливания энергии должна быть равна скорости прихода энергии через все шесть граней элемента.

Скорость прихода энергии за счёт теплопроводности определяется по закону Фурье. Плотность теплового потока в элемент в направлении оси х равна .

Скорость прихода энергии за счёт теплопроводности в направлении оси х через грань с площадью dydz равна

. (11.17)

Соотношения аналогичные (11.17) могут быть получены для скорости прихода энергии в направлении осей y и z.

Сумма трёх скоростей прихода энергии по осям x, y, z устанавливается равной скорости накапливания энергии в элементе, т.е.

, (11.17)

. (11.18)

.

Уравнение (11.18) называют уравнением энергии, которое описывает изменение температуры в движущейся жидкости.

Принимаем в (11.18) , , , а также постоянным коэффициент теплопроводности  и вводя обозначение

,

где а – коэффициент температуропроводности, ,

получим уравнение нестационарной теплопроводности в твёрдом теле при отсутствии внутренних источников теплоты

. (11.19)

Получили (11.19) уравнение теплопроводности Фурье. Решение этого уравнения – это температурное поле в теле .

Если температура твёрдого тела не меняется во времени (стационарная теплопроводность), то из выражения (11.19) получаем

. (11.20)

Т.е. получаем уравнение Лапласа, где – оператор Лапласа (лапласиан).

11.5 Условия однозначности (краевые условия). Уравнение теплообмена

Полученное дифференциальное уравнение конвективного теплообмена, уравнение сплошности (11.7), движения (или Навье-Стокса) (11.12) и энергии (11.18) описывают бесчисленное множество конкретных процессов конвективного теплообмена. Чтобы выделить определённый процесс конвективного теплообмена необходимо к этим дифференциальным уравнениям присоединить условия однозначности, которые состоят из:

1) геометрических условий, характеризующих форму и размеры тела или системы тел, в которой происходит данный процесс конвективного теплообмена;

2) физических условий, характеризующих физические свойства среды (, , а);

3) временных (или начальных) условий, характеризующих особенности процесса в начальный момент времени (для стационарных процессов они отпадают);

4) граничных условий (I, II, III, IV-рода), характеризующих особенность протекания процесса на границе раздела сред.

Система дифференциальных уравнений (11.7), (11.12) и (11.18) совместно с условиями однозначности составляют математическую формулировку краевой задачи или данного процесса теплообмена.

Основное уравнение конвективного теплообмена (11.1) имеет вид: .

Из него следует, что на поверхности или на стенке, согласно теории прилипания, скорость движения жидкости равна нулю, т.е. . Забегая вперёд, отметим, что у поверхности существует тонкий, заторможенный слой жидкости (гидродинамический пограничный слой), в котором теплота передаётся только путём теплопроводности согласно закону Фурье: . ()

где n – направление нормали к поверхности.

Согласно закону Ньютона-Рихмана – плотность теплового потока на поверхности пропорциональна разности температур поверхности и жидкости. . ()

Приравнивая () и () получаем:

. (11.21)

(уравнение теплообмена или теплоотдачи)

Для замыкания системы дифференциальных уравнений необходимо добавить уравнение состояния тела (для идеального газа или ).

До настоящего времени точного решения системы дифференциальных уравнений конвективного теплообмена не существует из-за сложности решения нелинейных дифференциальных уравнений второго порядка в частных производных – уравнения Навье-Стокса и энергий.

Имеется только приближённое решение для нескольких случаев конвективного теплообмена, не имеющих практического интереса (например, истечение жидкости из бесконечного объёма на перпендикулярную потоку плоскую пластину).

Большое значение для изучения конвективного теплообмена имеет эксперимент. Экспериментальное изучение сложных процессов теплообмена, зависящих от большого числа факторов, является трудоёмкой и дорогостоящей задачей. Поэтому при постановке экспериментов ставится задача получить данные не только для рассматриваемого экспериментального процесса, но и для подобного изучаемому.

Для упрощения уравнения движения Навье-Стокса используется теория пограничного слоя.