Для решения этого уравнения необходимо иметь краевые условия. Начальные условия.

1) , . .

Граничные условия: так как плоскость симметрии пластины проходит через , то

2) , при .

При на поверхности пластины граничные условия III-рода:

3) при . .

В соответствии с (9.2) общее решение (9.4) будет иметь вид: . (9.5)

Используя начальные и граничные условия для определения постоянных интегрирования , можно получить трансцендентное уравнение вида: , (9.6) . (9.7)

Уравнение (9.7) наиболее просто решается графически.

Из рисунка 9.3 видно, что имеется бесчисленное множество корней для каждого значения Bi. Найдём границы изменения числа Bi.

Если Bi  , то при заданном размере стенки и её материала, в этом случае ; при этом температуры стенки и жидкости оказались равными ,

а корни уравнения (9.7) имеют следующие значения

; ; ; …; ,

.

На практике , это случай когда .

Если Bi  0,    0. В этом случае избыточная температура: , т.е. теплоотдачи от поверхности пластины к жидкости нет, и корни уравнения (9.7)

,

где n­­ – порядковый номер корня.

Для каждого значения 0  Bi  , решение дифференциального уравнения (9.4) будем искать в виде:

. (9.8)

Определив , запишем окончательное решение уравнения теплопроводности (9.4):

(9.9)

(быстросходящийся ряд Фурье)

Решение (9.9) можно представить в обобщённых переменных:

, (9.10)

где – безразмерная координата;

– число подобия Фурье (безразмерное время).

Решения (9.10) представлены в виде простых и удобных номограмм, которые могут быть двух видов. Номограммы построены для двух случаев:

– центр пластины

– поверхность пластины

Зависимость (9.10) справедлива также для цилиндра и шара.

Для решения прямой задачи определения температуры в центре либо на поверхности пластины через какой-то момент времени после её охлаждения в среде с , при заданных размерах , материале пластины , и  находится . Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна:

.

В любом сечении температура находится с помощью решения (9.9).

9.3 Частные случаи охлаждения (нагрева) неограниченной пластины

Анализ решения дифференциального уравнения одномерной теплопроводности записанного для неограниченной пластины (9.9) в виде бесконечного, быстросходящегося ряда предполагает три характерных случая:

1. ( ). В этом случае с достаточной точностью можно ограничится первым членом ряда, и распределение температуры в неограниченной пластине будет иметь вид:

Так как распределение температуры в теле определяется как внутренним термическим сопротивлением, так и внешним, то для инженерных расчётов при в уравнении (9.9) можно ограничится первым членом ряда, так как термическое сопротивление , то температура на поверхности пластины становится равной температуре окружающей среды, т.е. .

2) ( ). Процесс выравнивания температуры в теле происходит значительно быстрее, чем отвод теплоты с поверхности пластины. Распределение температуры в этом случае показано на рисунке (9.7).

3) (Реальный случай).

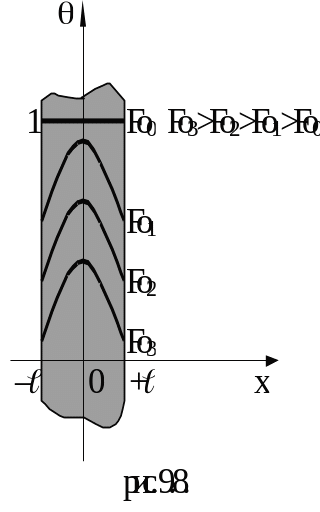
Каждому значению числа Bi отвечает своя совокупность корней уравнения (9.9).

Расход теплоты каждым м³ охлаждаемой пластины за время от до определяется по формуле:

,

где С – теплоёмкость материала пластины;

 – плотность пластины;

₀ – начальная избыточная температура;

 – средняя избыточная температура по толщине пластины в момент ₁.