9.4 Зависимость процесса охлаждения (нагрева) от формы и размера тела

Скорость распределения и изменение температуры в теле зависит от отношения поверхности тела к его объёму. Чем больше это отношение, тем больше скорость распространения температуры в теле. Это справедливо для любых значений Bi.

Для безграничной пластины, цилиндра, шара при уравнения температурного поля в безразмерных координатах:

,

,

.

При одинаковом определяющем размере и прочих равных условиях наибольшая скорость изменения температуры во времени будет наблюдаться для шара. У него больше отношение поверхности к объёму.

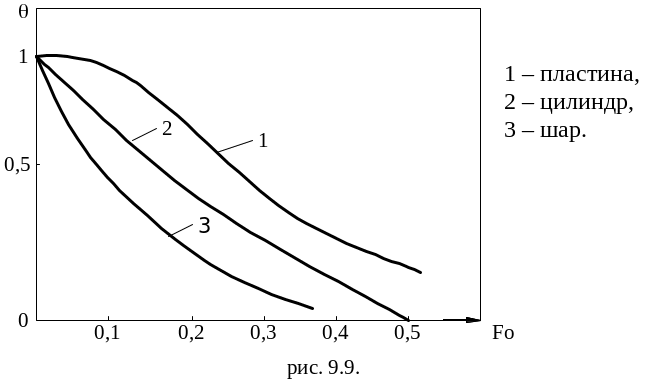
Если сравнить отношения поверхности тела к его объёму для пластины, цилиндра и шара, то их можно представить: .

Для тел конечных размеров (параллелепипеда, цилиндра конечного размера, и прямоугольного стержня) можно использовать номограммы для тел бесконечных размеров. Необходимо учитывать, что параллелепипед может быть образован пересечением трёх безграничных пластин с характерными размерами (x, y, z). Поэтому можно доказать, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.

Для параллелепипеда: ,

где: ; ; ,

Т.Е. Можно представить:

 

 .

Этот метод в теории теплопроводности называется теоремой о перемножении решений.

Для цилиндра конечной длины, полученного пересечением бесконечного цилиндра с пластиной , где z – высота цилиндра

.

_z, _r берутся по соответствующим номограммам для пластины и цилиндра.

Для длинного прямоугольного стержня (неограниченный параллелепипед). Результат пересечения двух пластин толщиной 2_х и 2_y.

.

9.5 Регулярный режим нагревания (охлаждения) тел

Анализ решения (9.9) показывает, что решение для тел любой формы имеет одинаковую структуру (сумма бесконечного ряда, члены которого расположены по быстро убывающим экспонентам). Например, для пластины:

(9.11)

коэффициент Ai не зависит ни от координат, ни от времени и находится из начальных условий. является функцией координаты (х), и его обозначаем через Ui. Экспонента убывает пропорционально времени . Комплекс – темп охлаждения.

Тогда (9.11) примет вид:

(9.12)

m – постоянное число причём оно будет изменятся в зависимости от номера индекса i. Причём m1  m2  m3  … < mn.

При малых значениях  (рис. 9.10) распределение температуры внутри тела зависит от начального распределения температуры в теле. В этом случае температурное поле будет определяться не только первым членом (9.12) но и последующими. Первый период охлаждения, при котором скорость изменения температуры внутри тела зависит от вида начального распределения температуры в теле, называется неупорядоченной стадией охлаждения.

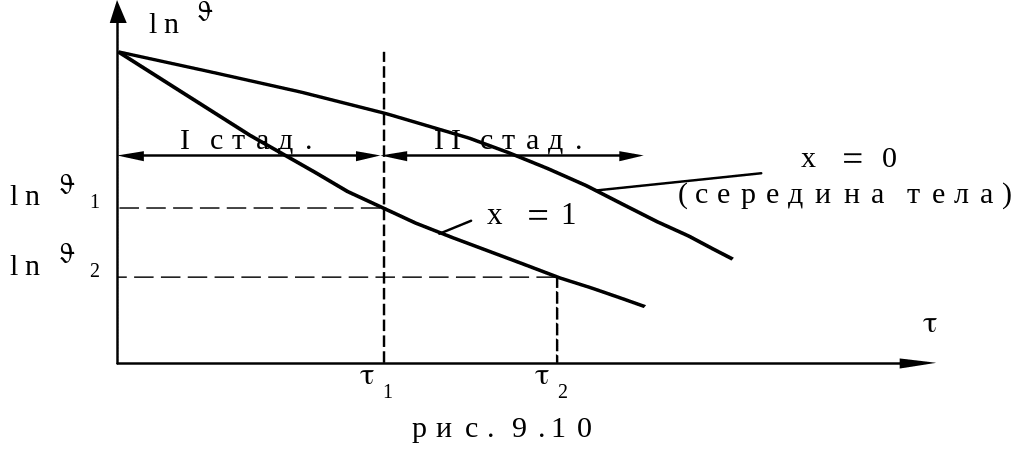
С увеличением времени последующие члены ряда (9.12) будут быстро убывать, т.е. ряд станет сходящимся. С момента начальные условия начнут играть второстепенную роль, и процесс охлаждения полностью определяется только граничными условиями на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами, и температурное поле описывается первым членом ряда.

. (9.13)

Логарифмируя (9.13) и опуская индексы получаем:

, или . (9.14)

Из (9.14) следует, что натуральный логарифм избыточной температуры для изменяется по линейному закону (рис. 9.10). При длительном охлаждении (, Fo), все точки охлаждаемого тела будут иметь температуру, равную температуре окружающей среды, наступает стационарное состояние. Рассмотрим вторую стадию охлаждения (регулярный режим). После дифференцирования левой и правой части (9.14) по времени мы получим, что:

. (9.15)

В левой части выражения стоит относительная скорость, изменение температуры, это есть величина постоянная и называется темпом охлаждения, которая не зависит ни от координаты, ни от времени; размерность .

Темп охлаждения характеризует относительную скорость изменения температуры в теле в зависимости от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.

Регулярный режим охлаждения характеризуется постоянным темпом охлаждения m во всех точках тела независимо от координаты и времени.

Если экспериментально определить изменение избыточной температуры во времени и построить зависимость в полулогарифмических координатах (рис. 9.10), то из неё для случая регулярного режима можно определить:

Зависимость m от физических свойств тела, его геометрических размеров и условий теплообмена на поверхности тела можно найти из анализа теплового баланса тела.

Изменение энтальпии тела равно потоку теплоты:

(9.16)

где  – плотность тела, ;

V – объём тела, м³;

v – средняя по объёму избыточная температура тела, К, С;

 – время, c.

За тоже время d вся теплота должна быть отведена с поверхности тела в окружающую среду за счёт теплоотдачи

, (9.17)

где – средний коэффициент теплоотдачи на поверхности тела.

.

Приравнивая (9.16) и (9.17) получаем:

.

Учитывая, что , и разделив левую и правую части уравнения на , получаем:

. (9.18)

Слева в (9.18) – темп охлаждения. Если обозначить через , то получим первую теорему Кондратьева: . (9.19)

Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела.

Коэффициент пропорциональности  называется коэффициентом неравномерности распределения температуры в теле. Он зависит от условий охлаждения на поверхности тела, т.е. от числа Bi.

Рассмотрим два случая:

1. Bi ( ).

В этом случае и распределение температуры в теле не зависит от размеров и физических свойств тела, поэтому усреднённая температура по поверхности будет равна усреднённой температуре по объёму , следовательно .

2. Bi ( ).

, и температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды, следовательно, , коэффициент неравномерности температуры .

При Bi () темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности a:

, (вторая теорема Кондратьева) (9.20)

Коэффициент К зависит от геометрической формы и размерности тела.

Для однородной пластины: ;  .

Трансцендентное уравнение для пластины было:

; при Bi; ; .

В (9.9) последующие корни не меньше чем предыдущие

Р₁  Р₂  Р₃  …

Д ля пластины коэффициент пропорциональности K

,

где  – толщина пластины

Коэффициент пропорциональности для шара:

.

Коэффициент пропорциональности для параллелепипеда:

.

Коэффициент пропорциональности для цилиндра конечной длины .

На основной теории регулярного режима разработаны различные экспериментальные методы определения теплофизических характеристик a, , c. ;

Для определения коэффициента теплопроводности , используется -калориметр в виде шара. Создаются условия теплообмена с конечным ; как правило, охлаждение на воздухе. При этих условиях определяется темп охлаждения.