11.2 Уравнение сплошности (или неразрывности) потока

В основе вывода дифференциального уравнения неразрывности лежит закон сохранения массы: сколько массы втекает в объём, столько же должно и вытекать.

Элемент объёма жидкости (dx, dy, dz) располагается в произвольной точке пространства с координатами (x, y, z) и движется вдоль линии тока со скоростью , проекции которой на оси будут равны _x, _y, _z. Состояние жидкости и свойство переноса в точке (x, y, z) обозначаем через Т, р, , .

Пусть плотность жидкости будет постоянной ( ), тогда масса жидкости в объёме (dx, dy, dz) должна сохраняться постоянной как при стационарном (скорость не изменяется во времени), так и при нестационарном режимах течения. Результирующий массовый расход жидкости через шесть граней должен быть равен нулю.

Массовый расход жидкости вдоль оси Х через единицу площади будет равен , .

Массовый расход жидкости через левую грань элементарного объёма будет равен , .

Разность массовых расходов жидкости через две перпендикулярные оси Х грани или скорость накопления массы в элементе (dx, dy, dz) будет равна

.

Аналогично для осей Y и Z:

, .

При условии постоянной плотности ( ) уравнение неразрывности потока получаем путём сложения скоростей накопления массы и приравнивая к нулю эту сумму массовых расходов через все шесть граней.

Т.к. , то, следовательно, . (11.5)

(дифференциальное уравнение сплошности потока для несжимаемой жидкости)

В векторной форме уравнение сплошности (неразрывности) записывается как . (11.6)

Для сжимаемой жидкости (т.е. для жидкости с переменной плотностью) разность между скоростью прихода массы в элемент и скоростью ухода массы из элемента равна скорости накапливания массы элементом объёма.

. (11.7)

(уравнение неразрывности для сжимаемой жидкости)

В векторной форме:

. (11.8)

Избыток массы обуславливается изменением плотности жидкости в объёме, равен изменению массы данного объёма во времени.

11.3 Уравнение движения (уравнение Навье-Стокса)

Для вывода уравнения движения используют закон сохранения количества движения.

Закон сохранения количества движения – изменение количества движения в элементе объёма жидкости (dx, dy, dz) равно результирующей всех внешних сил, приложенных к поверхности и объёму элемента.

Количество движения по определению равно произведению массы выделенного элемента жидкости на скорость его движения.

, – вектор количества движения.

Закон сохранения количества движения можно представить в векторной форме или в форме трёх скалярных уравнений. При выводе уравнения движения учитываем поверхностные силы на трёх из шести граней объёма. На каждой грани для описания полной силы, действующей на эту грань, достаточно одного нормального и двух касательных напряжений. Силы, обусловленные электрической природой, гравитацией и магнетизмом и их проекции на оси обозначаем через Х, Y, Z. Три нормальных напряжения _x, _y, _z обусловлены давлением и трением при растяжении элементов. Шесть касательных напряжений  обусловлены степенью сдвига, и только три касательных напряжения независимы. Касательные напряжения с одинаковыми, но расположенными в разном порядке индексами равны:

, , .

Сумму сил в направлении X, Y, Z, приложенных к элементу объёма можно представить в виде

.

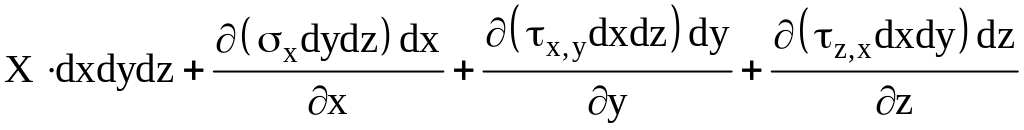Аналогично для осей Y и Z. Каждая из этих величин равна скорости изменения количества движения массы жидкости dxdydz, находящейся в данный момент в точке x, y, z.

Полная или субстанционная производная оценивает действительное ускорение, которое испытывает частица материи или субстанции проходя вдоль линии тока в поле скорости (рис. 11.1). Полная субстанционная производная для составляющей скорости вдоль оси ОХ будет равна

. (11.9)

Аналогично для и .

, (11.9)

. (11.9)

Скорость изменения во времени составляющих количества движения вдоль соответствующих осей OX, OY, OZ будет:

, , .

Тогда, три скалярных уравнения закона сохранения количества движения будут иметь вид:

(11.10)

Стокс предположил, что в движущихся жидкостях и газах напряжения пропорциональны не деформациям, как в твёрдых упругих телах (закон Гука), а скорости деформации (закон трения Стокса). Схема деформации элементов со сдвигом в плоскости X, Y показана на рис. 11.3.

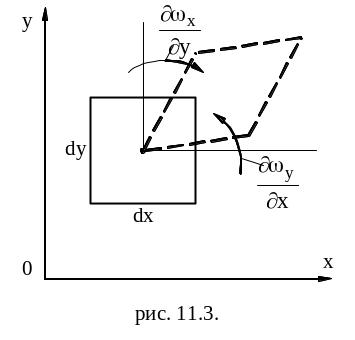
Для получения скорость угловой деформации умножим на вязкость:

,

,

.

Для нормальных напряжений _x, _y, _z, обусловленных растяжением элемента, используют зависимости вида:

(11.11)

Подставляя (11.11) и  в (11.10) мы получаем уравнение движения для несжимаемой жидкости или уравнение Навье-Стокса:

(11.12)

Если на движущийся поток жидкости действует сила гравитации, а нет электрических и магнитных сил, то массовые силы вдоль осей X, Y, Z будут равны:

, , ,

где –проекции вектора ускорения свободного падения на оси.

В векторной форме окончательное уравнение движения (или уравнение Навье-Стокса) для движущейся жидкости в гравитационном поле имеет вид:

, (11.13)

Уравнение Навье-Стокса подтверждает второй закон Ньютона: произведение массы на ускорение равно сумме сил. Т.е. уравнение баланса количества движения соответствует второму закону Ньютона.

Для частного случая, когда силами вязкого трения можно пренебречь для идеальной жидкости, уравнение Навье-Стокса превращается в уравнение Эйлера

. (11.14)

Из (11.14) для установившегося безвихревого движения в поле силы тяжести энергетический баланс для элементарной струи жидкости описывается уравнением Бернулли:

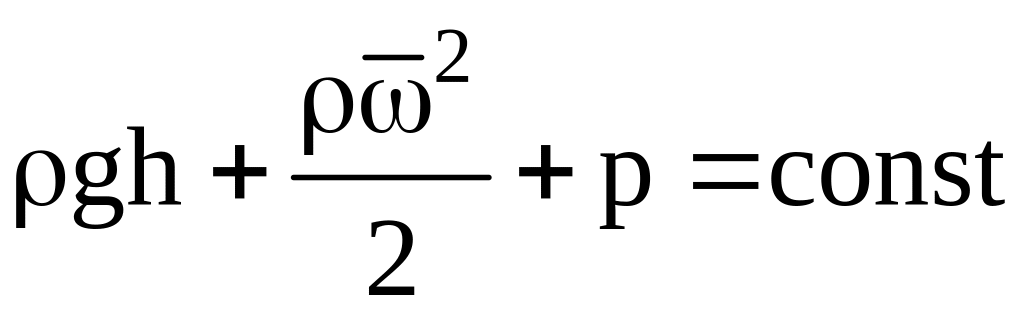, (11.15)

Уравнение Навье-Стокса (11.12) определяет характер распределения скоростей в однородном потоке с постоянной скоростью. Если заданы краевые условия, начальные и граничные, то 4 уравнения сплошности (11.8) и уравнение движения (11.12) дают распределение в пространстве и во времени 4-х величин: _x, _y, _z, р. Эти распределения являются решением конкретной задачи. Чтобы найти поле распределения температур или энтальпий рассмотрим уравнение энергии.