5. Метод приведения к треугольному виду.

Используя свойства, добьемся такой структуры определителя, при которой все его элементы, стоящие ниже главной диагонали, равны нулю. Тогда определитель будет численно равен произведению элементов, стоящих на главной диагонали.

6. Формула для ведущих элементов.

Если матрица представляется в виде , то левые верхние углы удовлетворяют соотношению

Для разных разложения подматриц «согласованы» друг с другом.

Объем параллелепипеда

Связь между определителем и объемом не очевидна, однако мы можем предположить для начала, что все углы прямые, т. е. грани взаимно перпендикулярны, и мы имеем дело с прямоугольным параллелепипедом. Тогда объем его равен просто произведению длин ребер .

Мы хотим получить ту же самую формулу с помощью определителя. С этой целью вспомним, что ребра параллелепипеда представляются строками матрицы . В нашем случае эти строки взаимно ортогональны, так что

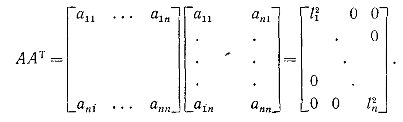
Величины суть квадраты длин строк матрицы, т. е. квадраты длин ребер, и нули вне диагонали получаются вследствие ортогональности строк. Переходя к определителям, получаем

Извлекая корень, мы и приходим к требуемому соотношению: определитель равняется объему. Знак при будет зависеть от того, образуют ребра правостороннюю систему координат вида или левостороннюю .

Если область не прямоугольна, то объем уже не равен произведению длин ребер. В плоском случае «объем» параллелограмма равен произведению длины основания на высоту .

Вектор длины есть разность между вектором второй строки и его проекцией на вектор первой строки.

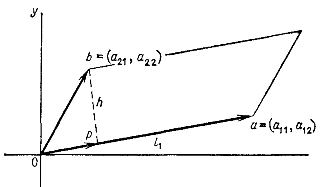
Площадь паралелограмма равна .

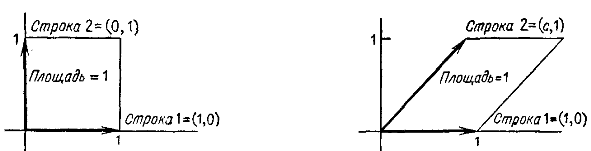
Площади квадрата и параллелограмма.

Первый представляет собой единичный квадрат, и его площадь, равна 1. Второй есть параллелограмм с единичными основанием и высотой; его площадь не зависит от «сдвига», даваемого коэффициентом , и равна 1.

4. Системы линейных уравнений, методы их решения (Крамера, Гаусса, матричный)

Рассмотрим систему m линейных уравнений с n неизвестными

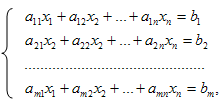i=1,…..,m; j=1,…..,n,          (1)

где a_ij- коэффициенты системы, x_j-неизвестные, b_i- свободные члены.

Совокупность чисел называется решением системы, если она обращает в тождество все уравнения системы. Если система имеет хотя бы одно решение, она называется совместной, если решений нет- несовместной.

Если совместная система имеет только одно решение, она называется определенной, если более одного - неопределенной.

Матрица A, составленная из коэффициентов системы и свободных членов

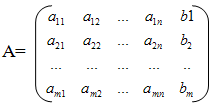
называется расширенной матрицей системы (1).

Для того, чтобы система (1) была совместной, необходимо достаточно, чтобы ранг расширенной матрицы A системы был равен рангу основной матрицы A. Если при этом он равен числу неизвестных, то система определенная.

Методы решения общих систем линейных уравнений.

Матричный метод.

Запишем систему (1) в матричном виде: AX=B, где

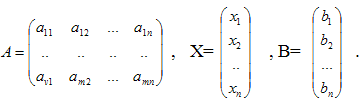
Рассмотрим случай, когда число неизвестных совпадает с числом уравнений. Тогда решение системы находится по формуле:

A^-1B=X

Формулы Крамера.

Составим матрицу A*, элементами которой являются алгебраические дополнения матрицы A :

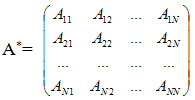
транспонируем ее и каждый элемент разделим на det A, получим матрицу

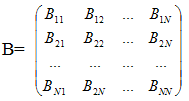, где B_ij=A_ij/det A, i=1,..,n; j=1,..,n.

Матрица B=A^-1. Тогда решение системы (1) можно найти по формулам

 j=1,..,n. Эти формулы называются формулами Крамера.

Метод Крамера и матричный метод применимы, если СЛУ имеет единственное решение.

 Метод Гаусса.

Рассмотрим систему m линейных уравнений с n неизвестными

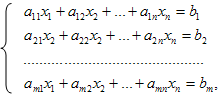i=1,…..,m; j=1,…..,n,                     (1) Пусть . Разделим все члены первого уравнения на :

                                                               (2) где (j =1,2…n + 1),                                                                      (3)

Рассмотрим i-е уравнение системы(1):

                                                            (4)

Для исключения из этого уравнения х₁ умножим уравнение (2) на и полученное уравнение вычтем из уравнения (4). Тогда будем иметь

                                                                    (5)

где                                                     (6)

Таким образом, получаем укороченную систему

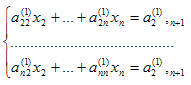                                                                  (7)

коэффициенты которой определяют по формулам (6).

Если ее ведущий коэффициент , то из системы (7) указанным выше приемом можно исключить неизвестное х₂, причем новые коэффициенты будут вычисляться по формулам типа (6) и т.д. Эта часть вычислений называется прямым ходом метода Гаусса.

Для определения неизвестных х₁,х₂,...х_n рассмотрим уравнения

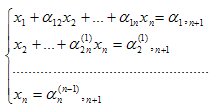                                                              (8)

Отсюда последовательно находим неизвестные (обратный ход):

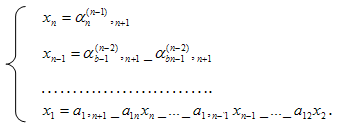                                (9)

Заметим ,что операции (9 )выполняются без деления. Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.

Однородные системы линейных уравнений.

Если свободные члены системы (1) равны нулю, то система называется однородной.

Для того, чтобы однородная система n линейных уравнений с n неизвестными обладала ненулевыми решениями, необходимо и достаточно, чтобы ее определитель был равен нулю.

Для решения однородных систем линейных уравнений удобно пользоваться методом Гаусса.